
ここでは
「正負の数」を使っての
「かけ算」「わり算」についてやっていきましょう
まずは言葉の説明です
「乗法(じょうほう)」
「除法(じょほう)」と読みます
正負の数の乗法

⑴では
まず「かけ算」を
「たし算」で考えてみます
(−4)が3こあるとき
(−4)×3=(−4)+(−4)+(−4)
と考えることもできますね
そうすると
答えは(−12)となります
(−12)は
「−」はそのままで
(絶対値4)に3をかけている
ことが分かりますね
⑵は符号は「−」
値は(絶対値5)×2となります
⑶は「(−3)倍」と考えると
難しいので
順番を入れ替えています
さあ⑷
「(負の数)×(負の数)です」

少しややこしいので、ゆっくり見ていきましょう
計算式を縦に見てください
×の後の( )の数を
(+2)→(+1)→ 0 →(−1)→(−2)と
「1」ずつ小さくしています
そうすると
出てくる答えは
「3」ずつ大きくなっています
そうすると
(−3)×(−1)の答えは
(−3)× 0 = 0 より
「3」大きくなり「+3」となります
では、乗法のルールをまとめましょう
特に(−)×(−)=(+)は
あまり深く考えると難しいので
ルールとして
覚えてしまいましょう
正負の数の除法

「わり算」は「かけ算」
と同じように考えることができます
⑶のように
「わり算」→「かけ算」にすると
考えやすいですね
逆数

⑴は慣れてきたら
2段目の(−0.2)×3は
頭の中でやってしまいましょう
⑵の答えですが
数学では分数の答えは
「仮分数」のままで大丈夫です
⑶は「分数のわり算」です
算数と同じように
「÷」の後の
分母と分子を反対にして
「×」をします
ここで新しい用語です
正負の数の乗除計算
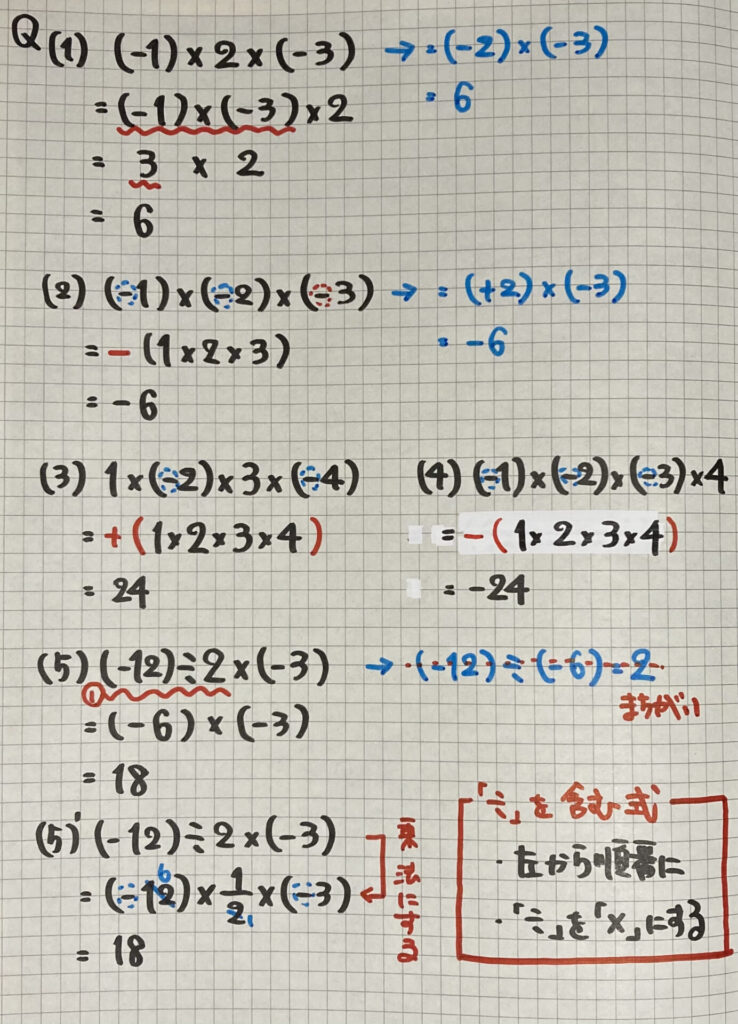
⑴は2と(−3)の場所を
入れかえています
⑵⑶⑷を見ると分かるように
式の中の(負の数)の個数で
答えの「符号」が決まります
あとは「絶対値」を計算するだけですね
⑸はよく間違ってしまう計算です
乗除(かけ算とわり算がある)計算は
「左から順番に」計算しましょう
⑸’のように
数学では「わり算」を「かけ算」に
することが多くなります
そうすると
⑸のように
間違えなくなるので
これからは
「わり算」は「かけ算」で
計算するようにしましょう
累乗と分配法則

最後に新しい
「累乗(るいじょう)」
という考え方です
⑵の累乗ですが
「5」だけを2回かけます
「符号」はそのままです
⑶の累乗ですが
( )を2回かけます
累乗は
すぐ左のものをかけてください
⑵は「5」
⑶は( )なので(−5)です
あとは、おまけです
整数で使えた
計算の工夫(分配法則)は
もちろん「正負の数」でも
使うことができますよ
「符号」には気をつけましょう
正負の数の乗法 除法のまとめ

・乗法…「かけ算」のこと
・除法…「わり算」のこと
・正負の数の乗法のルール
(除法も同じ)
- (+)×(+)=(+)
- (−)×(+)=(−)
- (+)×(−)=(−)
- (−)×(−)=(+)
・逆数(ぎゃくすう)
$\frac{△}{○}$→$\frac{○}{△}$
「分母」と「分子」を反対にしたもの
「符号」はそのままなので注意です
・正負の数の乗除計算
「負の数」の個数が
- (偶数)のとき→答えは(+)
- (奇数)のとき→答えは(−) になる
・累乗(るいじょう)
$2^4$
「2の4乗(じょう)」と読みます
「2」の右上の
「4」を「指数(しすう)」といいます
意味は
$2^4=2×2×2×2$
を表しています
・累乗が入った乗除計算の順番
- 累乗の計算
- 「×」「÷」
- 「+」「−」
以上、「数学嫌いな人が、
数学を楽しく好きになって欲しい」
かずのかずぶろぐでした








