前回は
相似を使った
「平面図形」の
「面積比」について
学習しました
【中3数学】「相似比と面積比」の問題 どこよりも簡単な解き方・求め方前回は、図形の問題でよく利用する「角の二等分線定理」「中点連結定理」を学習しました 今回は、「相似比」を使った「面積比」について一緒に見ていきましょう...
今回は
「立体(空間図形)」の
「表面積・体積の比」
について
一緒に見ていきましょう
相似な立体の表面積・体積の比
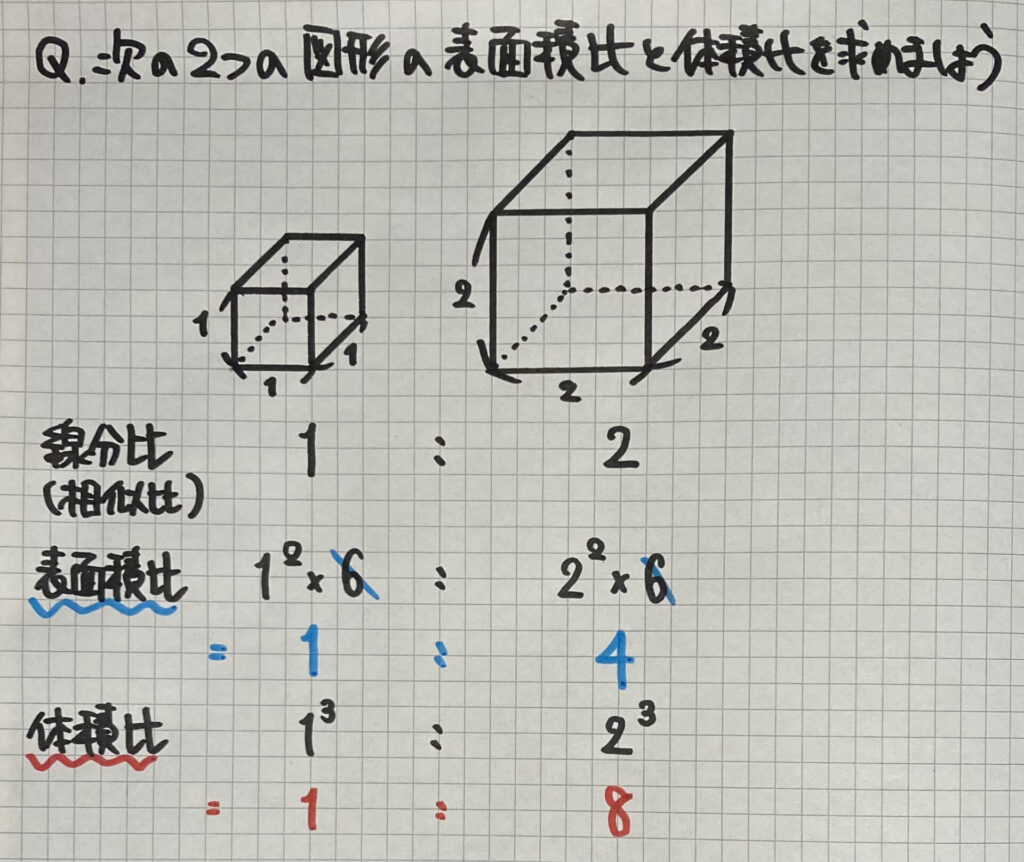
まずは
立方体で
考えてみましょう
表面積は
前回の面積と同じく
「表面積の比」は
「線分比」の「2乗」になりました
次に「体積」です
立方体の体積は
「一辺×一辺×一辺」
で求めるので
「体積の比」は
「線分比」の「3乗」になりました

次に
「球」でも
確認してみます
球の公式
大丈夫でしょうか
立方体と
同じように
- 表面積の比→線分比の「2乗」
- 体積の比→線分比の「3乗」
になります
このように
どのような図形でも
ことが分かりました
相似な円錐
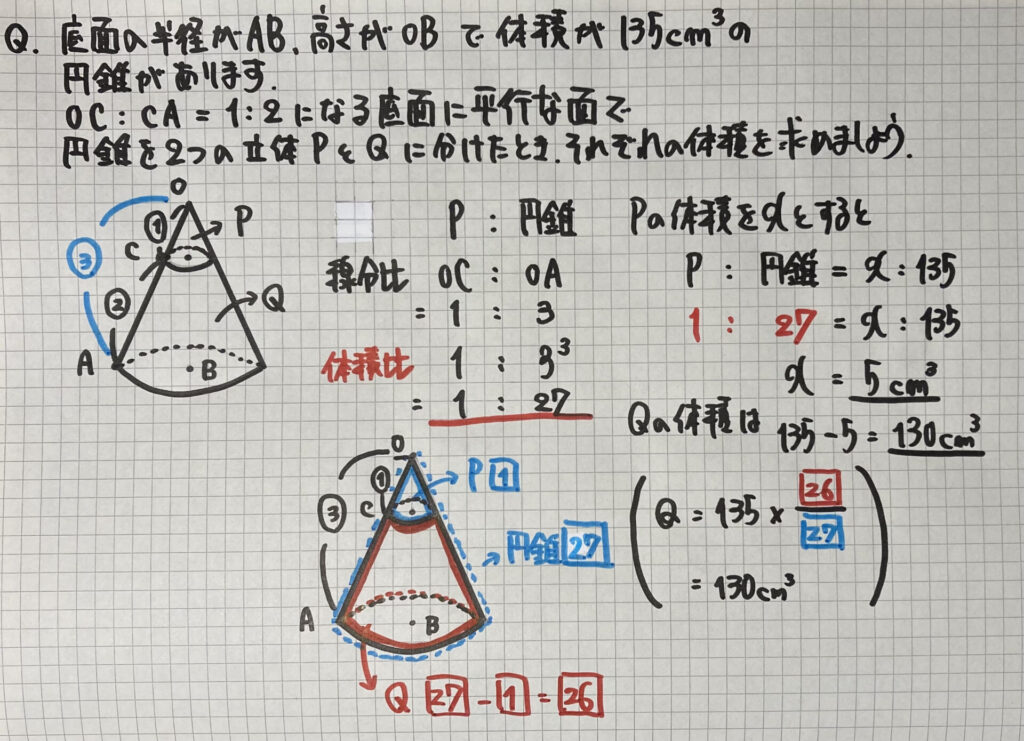
先ほどの
「体積の比は、相似比の3乗」
を利用して
円錐の体積を
求めましょう
ノート右下に
まとめていますが
Qの体積について
体積比(割合)で
考えると
P:円錐=1:27 なので
P:Q
=1:(27-1)=1:26 より
Q=円錐×$\frac{26}{27}$
で求めることができました
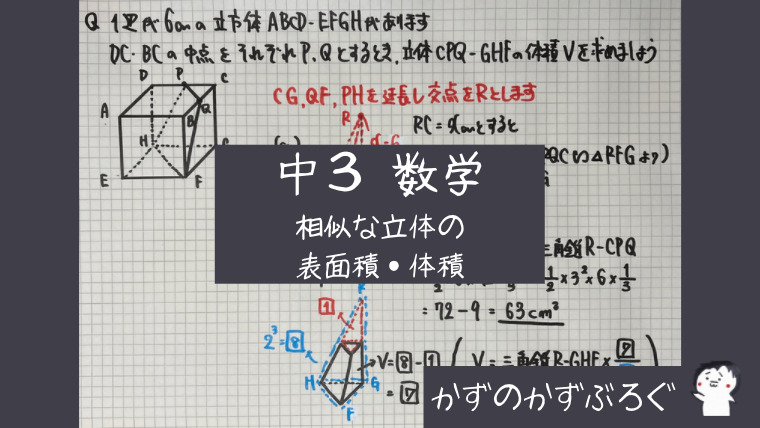
相似な三角錐
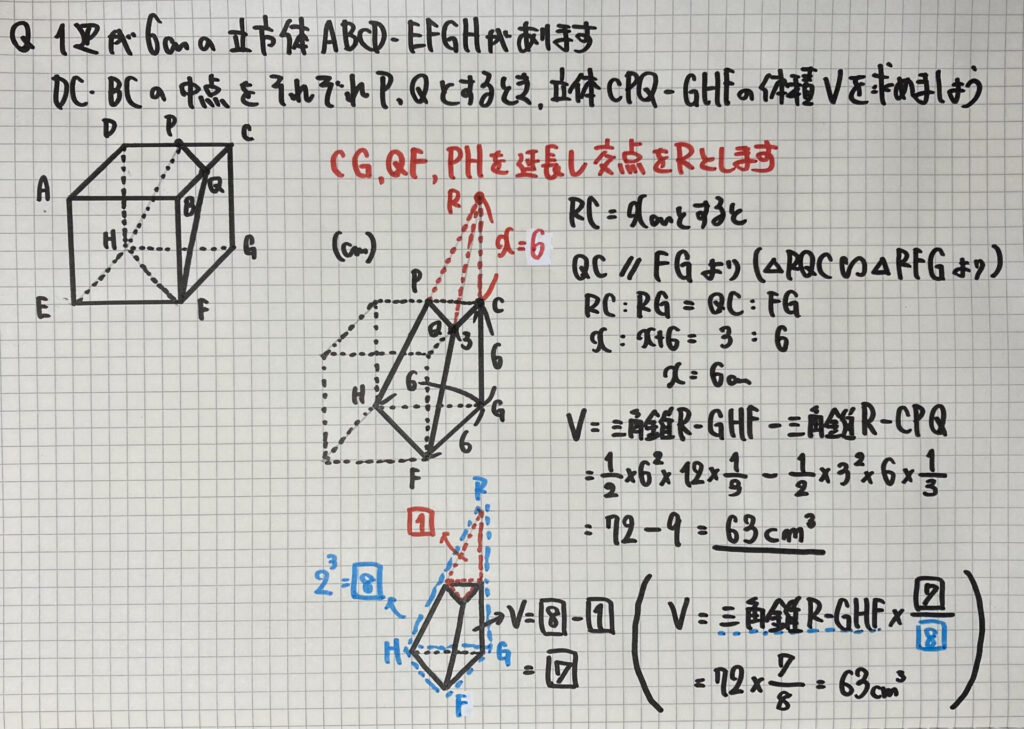
立体 CPQーGHF
の形は大丈夫でしょうか
ノートにあるように
「三角錐から、
上部の小さな三角錐を除いた立体」
「(三角錐RーGHF)−(三角錐RーCPQ)」
です
このような立体を
「三角錐台」と言います
問題の最初の図形の
ままで考えるのは
難しいので
CG、QF、PH
を延長して三角錐を作ります
ここがこの問題のポイントです
- QC//FG(平行線と線分の関係)
- △PQC∽△RFG
のどちらかを利用して
RCを求めましょう
あとは
- (三角錐RーGHF)−(三角錐RーCPQ)
- 体積比(割合)を利用
で体積を
求めることができます
相似な立体の表面積・体積のまとめ

・どのような図形でも
「表面積の比」は
「相似比」の「2乗」になり
「体積の比」は
「相似比」の「3乗」になる
・三角錐台の図形
線分を延長して「三角推」を作る
かずのかず
以上、「数学嫌いな人が、
数学を楽しく好きになって欲しい」
かずのかずぶろぐでした