今回から「円の性質」について
学習していきます
まずは新しい
「円周角」という言葉
「中心角」や「弧」との
関係を理解していきましょう
円周角と中心角
①
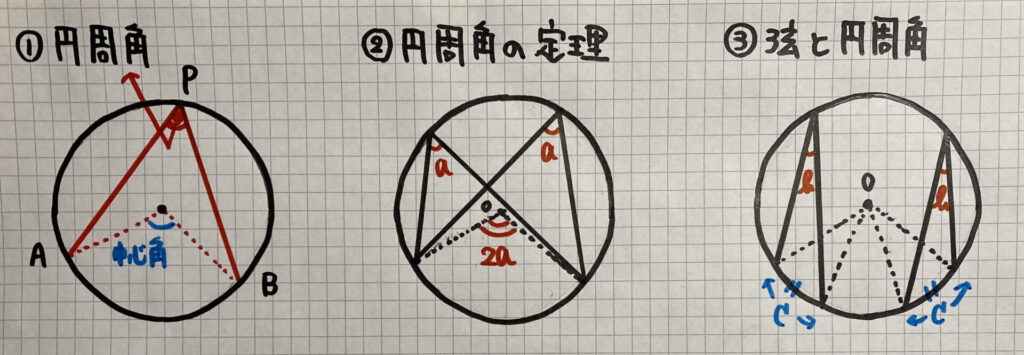
円Oで$\stackrel{\huge\frown}{AB}$を除いた
円周上に点Pをとるとき
$\angle APB$を$\stackrel{\huge\frown}{AB}$
に対する円周角といいます
②
③ ×「弦」→○「弧」です(失礼しました)
円周角の定理の証明
①「円周角の内側」に円の中心Oがあるとき
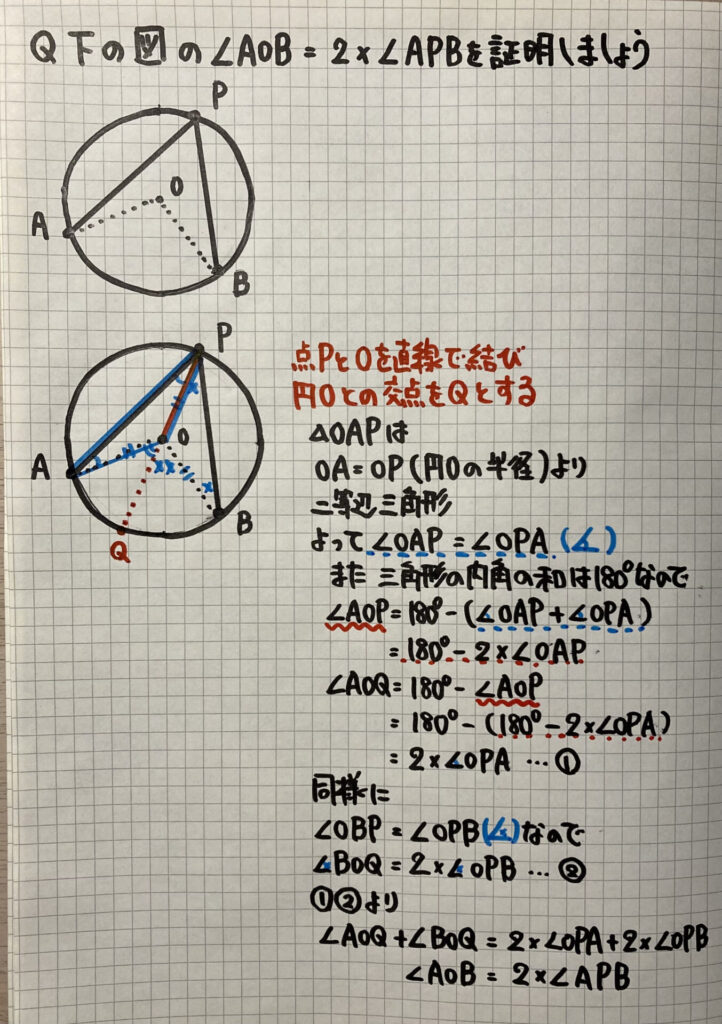
点Pと点O(中心)を直線で結ぶ
↓
円の半径は全て等しいので
↓
△OAPと△OBPは
二等辺三角形になる
↓
三角形の外角の性質を利用しましょう
次に円の中心の場所が違う
2つの場合についてです
考え方は①と同じなので
簡単に見ていきます
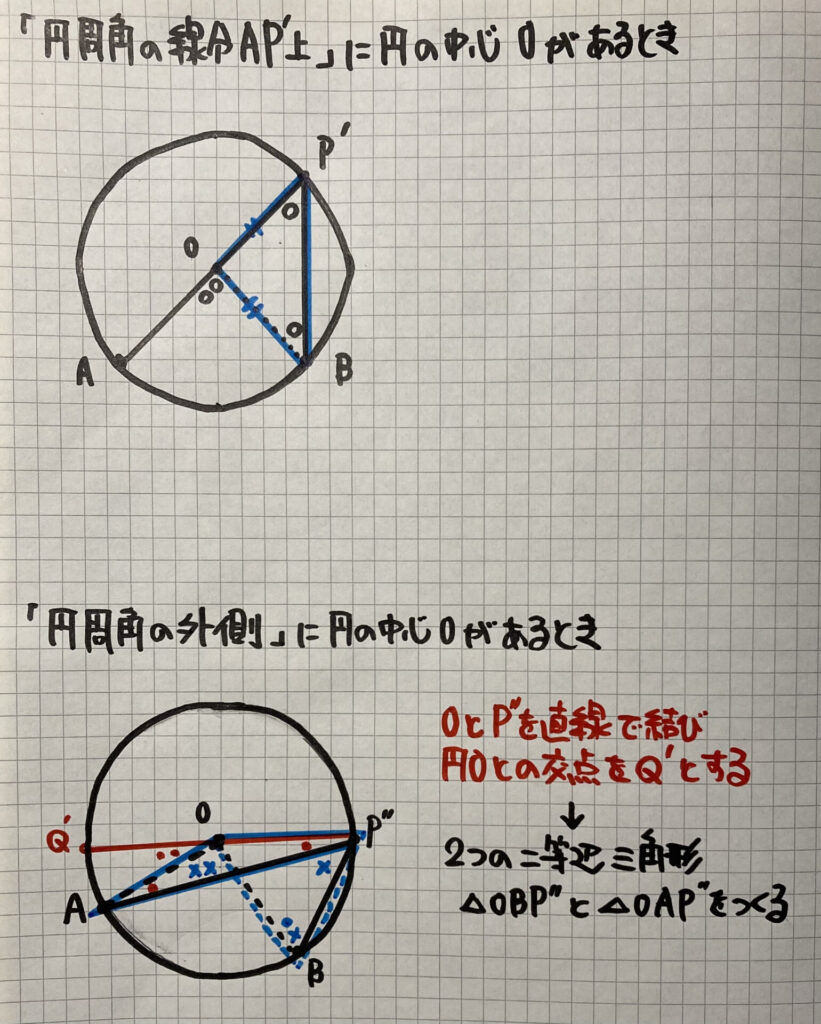
②「円周角の線分上」に
円の中心Oがあるとき(上の図)
OB=OP’(円Oの半径)より
△OBP’は二等辺三角形
あとは三角形の内角(外角)の
性質を利用して
$\angle AOB=2×\angle AP’B$
③「円周角の外側」に
円の中心Oがあるとき(下の図)
△OAP”は二等辺三角形より
$\angle OAP”=\angle OP”A$
$\angle Q’OA=2×\angle OP”A$
△OBP”は二等辺三角形より
$\angle OBP”=\angle OP”B$
$\angle Q’OB=2×\angle OP”B$
$\angle AOB$
$=\angle Q’OB−\angle Q’OA$
$=2×\angle OP”B−2×\angle OP”A$
$=2×(\angle OP”A+\angle AP”B)−2×\angle OP”A$
$=2×\angle AP”B$
円周角の練習問題
まずは基本的な問題です
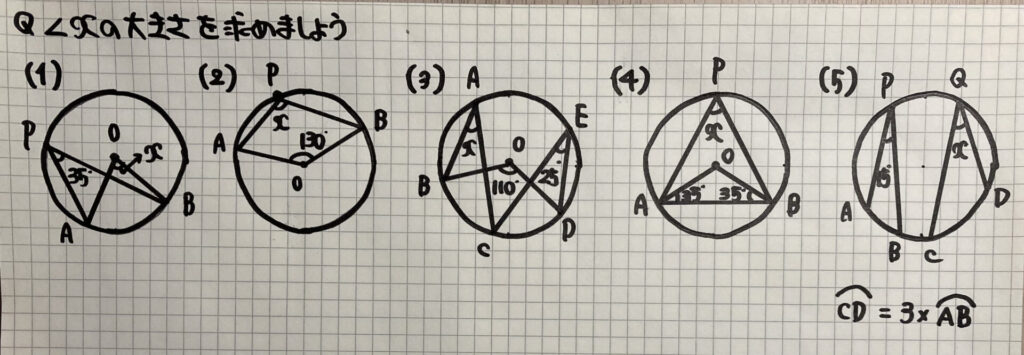
解き方はこちら
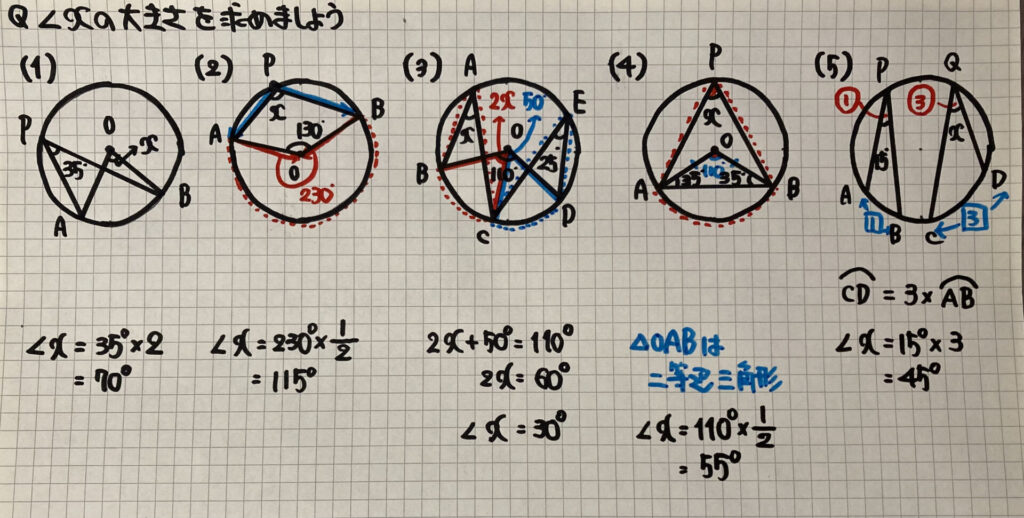
(1)中心角は円周角の2倍を利用します
(2)$\angle x$は
$\stackrel{\huge\frown}{AB}$の円周角です
$\stackrel{\huge\frown}{AB}$の中心角は
(3)$\stackrel{\huge\frown}{BC}$と$\stackrel{\huge\frown}{CD}$
の円周角から中心角を求めて
方程式を作りましょう
(4)0A=0B(円Oの半径)より
△OABは二等辺三角形なので
$\angle AOB=180°−35°×2=110°$
を求めることができます
(5)円周角の定理の
「1つの円で等しい弧に対する
円周角の大きさは等しい」
の考え方を利用すると
弧の長さが、2倍3倍4倍…になると
円周角の大きさも、2倍3倍4倍…になる
つまり
円周を等分する点の問題
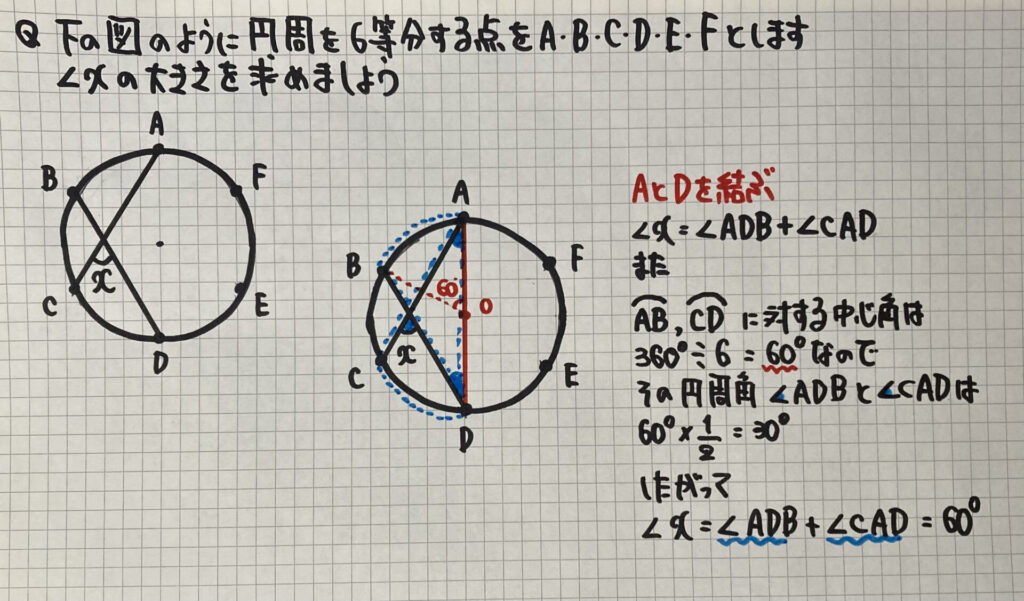
- 等分する弧1つの中心角を求める(360°÷○)
- 求める角に関する円周角を作る
(慣れてくれば、等分する
弧1つの円周角→180°÷○を使っても良いです)
円周角と中心角のまとめ

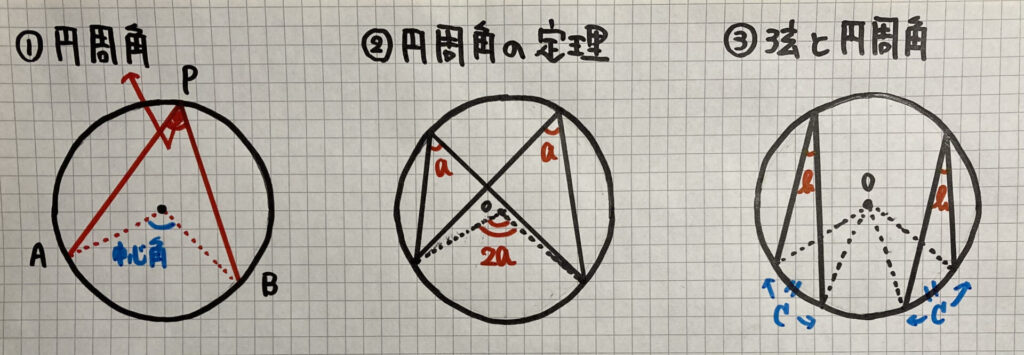
①円Oで$\stackrel{\huge\frown}{AB}$を除いた
円周上に点Pをとるとき
$\angle APB$を$\stackrel{\huge\frown}{AB}$
に対する円周角といいます
②円周角の定理
・1つの弧に対する
円周角の大きさは
その弧に対する
中心角の大きさの半分である
・同じ弧に対する円周角の大きさは等しい
③×「弦」→○「弧」です(失礼しました)
・1つの円で
等しい弧に対する
円周角の大きさは等しい
・1つの円で
等しい円周角に対する
弧の長さは等しい
- 等分する弧1つの中心角を求める(360°÷○)
- 求める角に関する円周角を作る
(慣れてくれば、等分する
弧1つの円周角→180°÷○を使っても良いです)
以上、「数学嫌いな人が、
数学を楽しく好きになって欲しい」
かずのかずぶろぐでした