前回は
図形の問題で
よく利用する
2つの定理
- 「角の二等分線定理」
- 「中点連結定理」
を学習しました
今回は
相似比を使った
面積比について
一緒に見ていきましょう
相似比と面積比
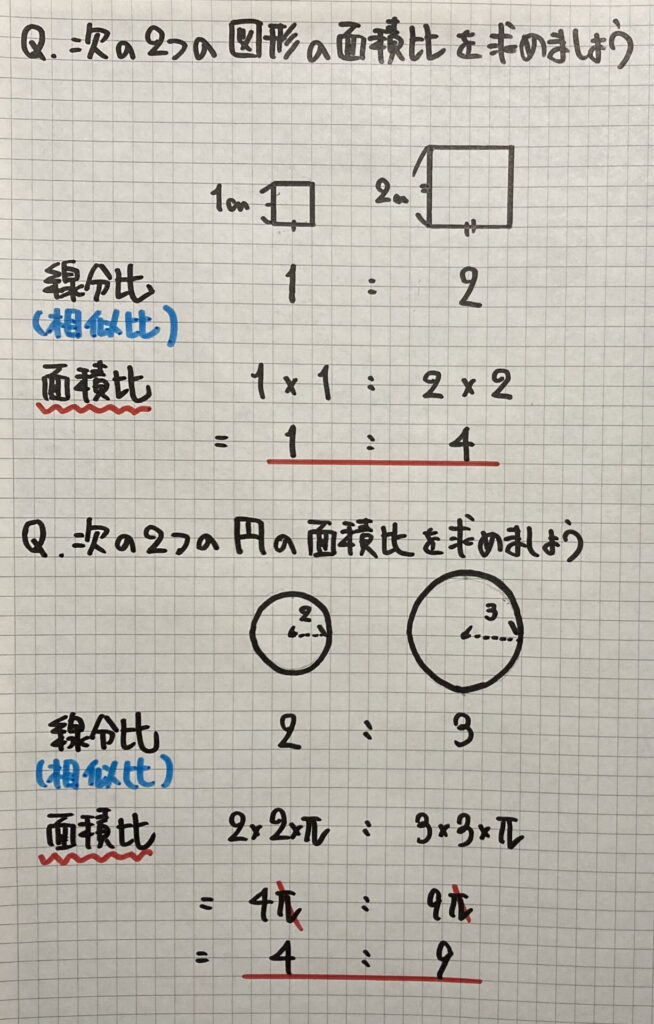
まずは
「相似比」と
「面積比」の関係に
ついて実際に
図形を使って
見ていきましょう
最初は正方形です
正方形の面積は
「一辺×一辺」
で求めることができますね
「相似比」は
「線分比」と等しいので
「面積比は、線分比の2乗」
ことが分かりますね
次に
「円」でも
確かめてみます
「面積=半径×半径×$π$」
で求めるので
正方形と同じように
「面積比は、線分比の2乗」
になります
このように
どのような図形でも
ことを
確認しておきましょう
相似な三角形と四角形
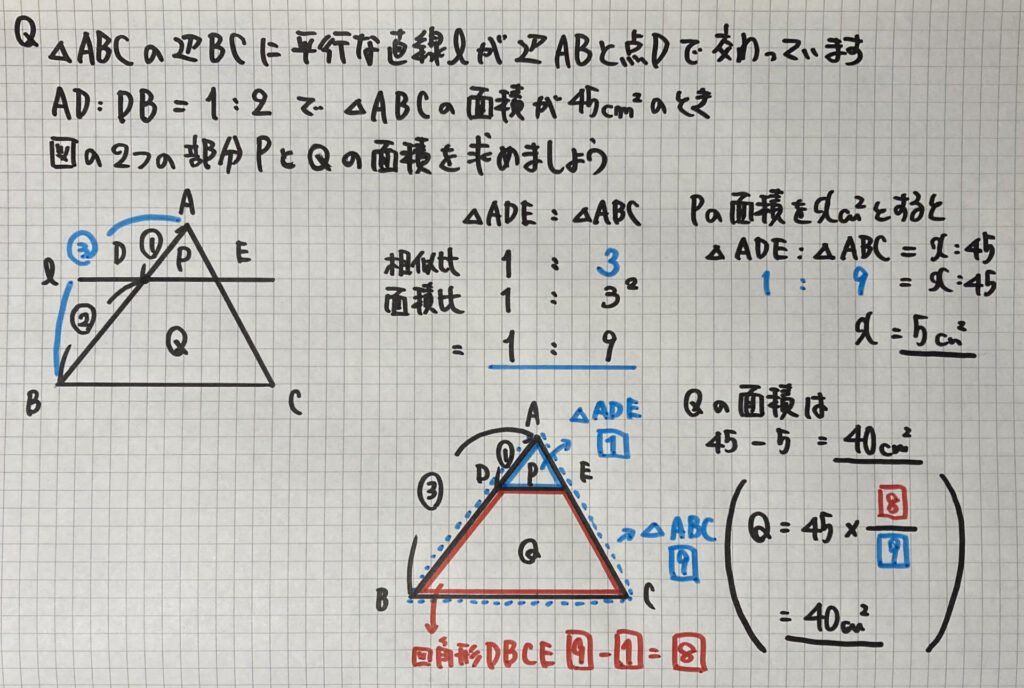
先ほどの
「面積比は、相似比の2乗」
を利用して
三角形の面積を
求めましょう
ノート右下に
まとめていますが
Qの面積について
面積比(割合)で
考えると
△ADE:△ABC=1:9なので
△ADE:四角形DBCE
=1:(9-1)=1:8 より
Q=△ABC×$\frac{8}{9}$
で求めることができますね
平行四辺形の「線分と面積の比」
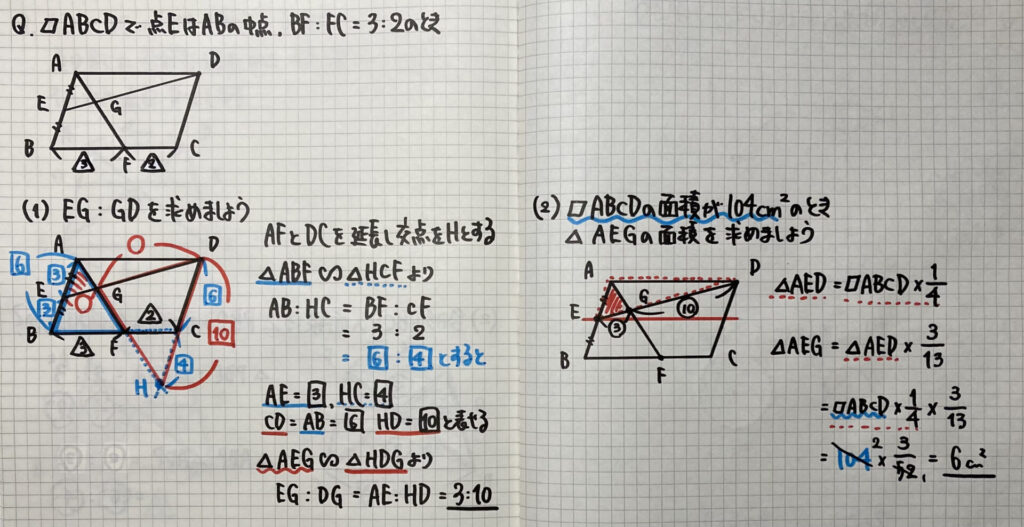
テストでよく出る
「平行四辺形」です
(1)の「線分比」
ですが
平行四辺形
↓
平行線
↓
平行線と線分比
なので
- ピラミッド型
- 砂時計型
を探します
ノートの問題の
ように
砂時計型の一部
がある場合
(2)の「面積比」
ですが
△AEGと△AGDは
台形の線分と面積

平行な線分
「AD」と「QR」と「BC」
に注目して
- ピラミッド型
- 砂時計型
を探しましょう
(1)は
砂時計型
△APD∽△CPBから
DP:BP=AD:CB=4:6=2:3
を求めて
ノートにまとめた
「2組の相似の三角形」
を利用して
求めましょう
(2)の
面積比は
- △PBC:△PDA(相似比の2乗)
- △ABP:△ADP(底辺比)
- △CDP:△CPB(底辺比)
に気をつけて
求めましょう
相似比と面積比のまとめ

・相似な図形の面積比
「面積比」は
「相似比」の「2乗」になる
・平行四辺形と相似
平行四辺形
↓
平行線
↓
平行線と線分比
なので
- ピラミッド型
- 砂時計型 を探す
・平行四辺形の線分比
砂時計型を作るために
求める線分と
「交わっている線分を延長」
しましょう
砂時計型を作るために
求める線分と
「交わっている線分を延長」
しましょう
・相似では無く、頂点共有の三角形の面積比
「高さ」が等しい三角形なので
「面積比=底辺比」になる
以上、「数学嫌いな人が、
数学を楽しく好きになって欲しい」
かずのかずぶろぐでした