中3数学

【中3数学】「関数$y＝ax^2$」の問題　どこよりも簡単な解き方・求め方

  /

「関数」は

中1で「比例」

中2で「一次関数」

を一緒にやりましたね

【中1数学】「比例の式とグラフ」の問題　どこよりも簡単な解き方・求め方今回は「比例」です「算数」でも学習したのは覚えてますか？「数学」なので「負の数」が出てくるので気をつけていきましょうね　比例の前に、まずは「関数」「変数」「変域」について見ていきましょう...
【中2数学】「一次関数 変化の割合」の問題　どこよりも簡単な解き方・求め方今回は、中1で出てきた「関数」の1つ「一次関数」の「式」と「変化の割合」について学習します　中1で学習した「比例」に似ていますが、少し違いますので一緒に見ていきましょう...

中3では

「$y＝ax^2$

(二乗に比例する関数)」

を学習します

「二次関数」と呼ばれる

こともありますが

厳密には

「二次関数」は

高校数学の範囲に

なるので

楽しみにしておいて

くださいね

では一緒に

やっていきましょう

目次
  1. 「関数$y＝ax^2$」とは
  2. 「$y＝ax^2$」の式を求める
  3. 関数$y＝ax^2$のまとめ

「関数$y＝ax^2$」とは

ノートにもありますが

円の面積

＝半径×半径×円周率($π$)

(＝$π r^2$)

ですね

（1）の表を

見てください

$xが、2倍　3倍$…になると

$yは、2^2倍　3^2倍$　…になる関係

になっていますね

どこかで

学習した内容に

似ていますね

そうです

比例

ともなって変わる2つの数（量）で

一方が2倍 3倍…になると、もう一方も2倍 3倍…になる関係

ですね

ではまとめましょう

$y＝ax^2$

（2乗に比例する関数）

ともなって変わる2つの数（量）で

一方が、$2倍　3倍$…になると

もう一方は、$2^2倍　3^2倍$　…になる関係

$\frac{y}{x^2}＝a（一定）$

($a$は比例定数)

（2）（3）は

「比例」や

「一次関数」と

同じように

(代入して)

解いていきましょう

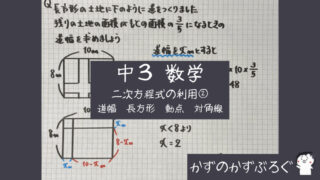
練習問題

関数の問題を

解くポイントは

$x$と$y$の

「単位」に注目する

今回は

$y＝3x^2$の式に

  • 「秒」…$x$
  • 「m」…$y$

を代入しましょう

代入してできた

「二次方程式」を

解くと

解は「2つ($x＝±4$)」

ありますが

$x$の単位は

「秒(時間)」より

$x>0$なので

求める解は

$x＝4$

「4秒後」です

「$y＝ax^2$」の式を求める

問題に

「$yはxの2乗に比例し…$」

→「$y＝ax^2$」を用意する

あとは

今までの「関数」

と同じように

「$x$や$y$」を

代入しましょう

（2）は

$x$が「2つ」あります

「$y＝ax^2$」

→$x$が「2つ」ある

（$y$は$x$の二次式なので）

関数$y＝ax^2$のまとめ

・$y＝ax^2$

（2乗に比例する関数）

ともなって変わる2つの数（量）で

一方が、$2倍 3倍…$になると

もう一方は$y$は、$2^2倍　3^2倍…$になる関係

$\frac{y}{x^2}＝a（一定）$

($a$は比例定数)

・問題文に「$yはxの2乗に比例し…$」

「$y＝ax^2$」を用意する

かずのかず

以上、「数学嫌いな人が、

数学を楽しく好きになって欲しい」

かずのかずでした

RELATED POST