今回は
「柱体」「錐体」「球」の
「表面積」
の求め方を学習します
では、一緒に
やっていきましょう
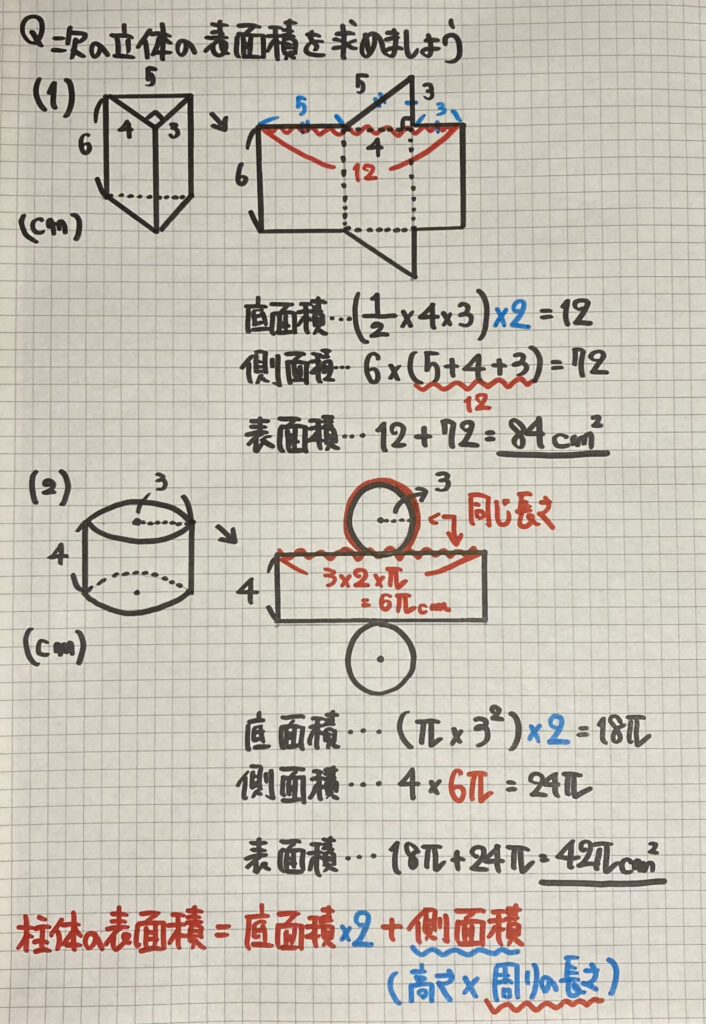
錐体の表面積

「角柱」の時と
同じように
「展開図」を書くと
求めることができます
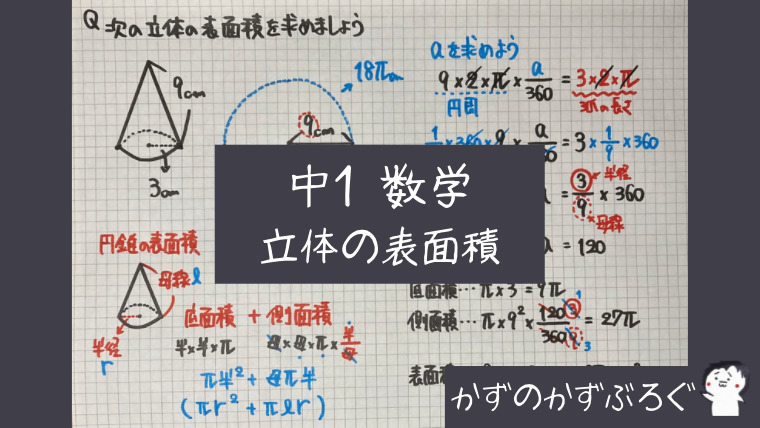
円錐の表面積
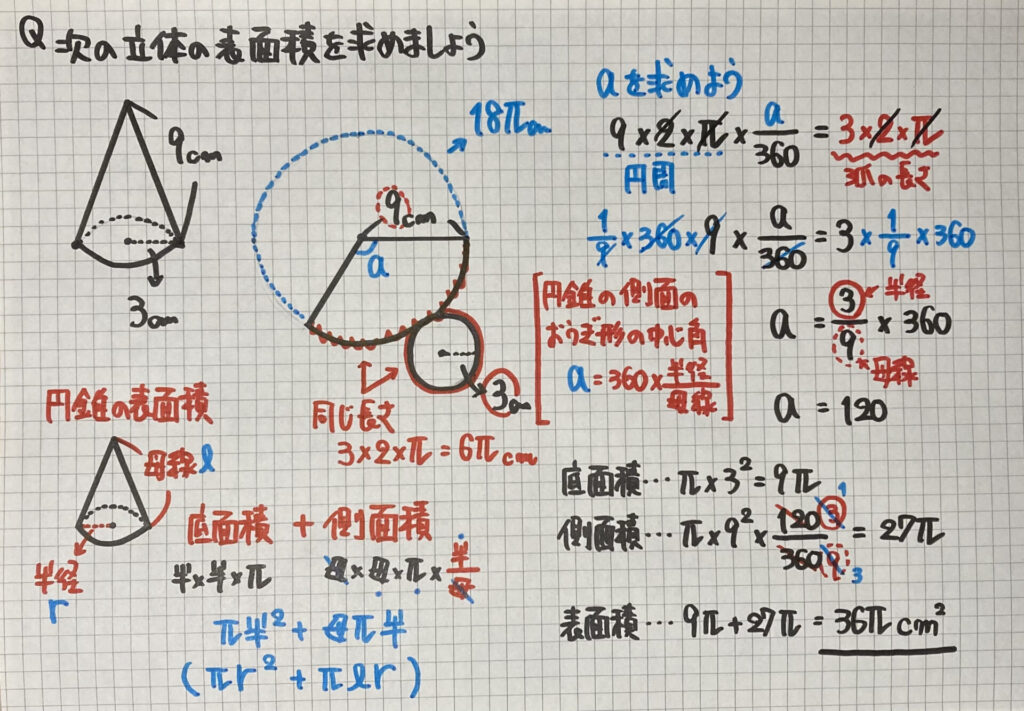
今回の単元で
「一番重要な問題」です
まず「円錐」の
「展開図」ですが
「円」と「おうぎ形」
になります
ここで重要なのが
おうぎ形の
「中心角」
です
ノートの右を
見てください
「円柱」の時と
同じように
になります
これを使って
中心角を$a$として
方程式を作り
求めています

毎回、こんな計算をするのは
大変ですね…
$a=\frac{3}{9}×360$
この式に注目しましょう
この$\frac{3}{9}$は
おうぎ形の
円の割合(どれだけか)を
表しています
そして
- 分母の「9」は円錐の「母線」
- 分子の「3」は底面の「半径」
になります
これを使うと
で求めることができます
さらに
側面積(おうぎ形)
を求める時の
$π$×半径×半径×$\frac{中心角}{360}$の
「$\frac{中心角}{360}$」の
代わりに
割合である
「$\frac{半径}{母線}$」を
使うことができます
この公式は
とても重要なので
しっかり確認しておきましょう
練習問題
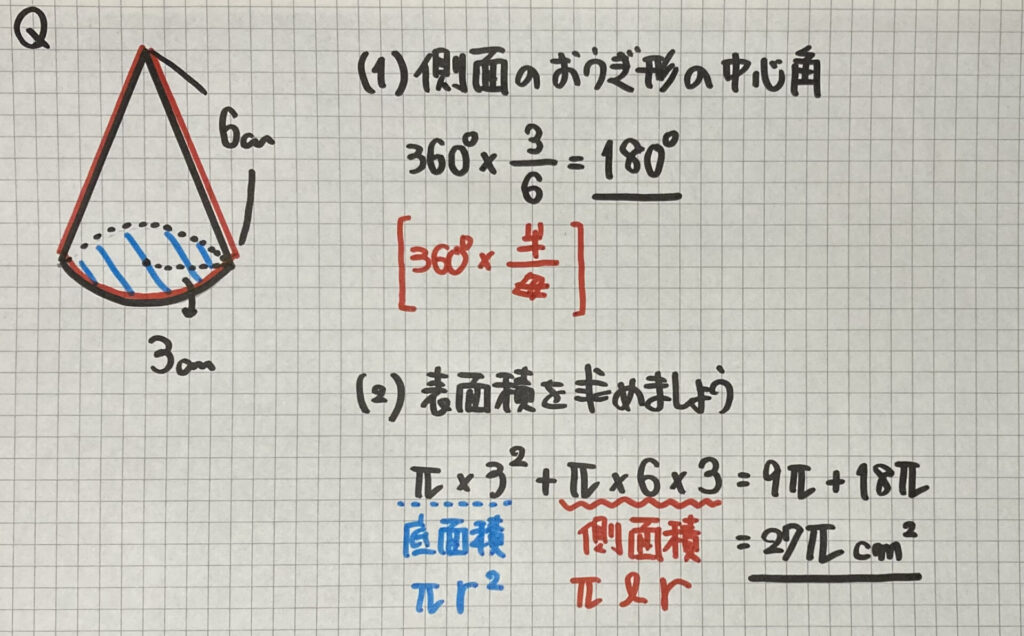
公式を使うと
「展開図」を
書かなくても
答えを求めることが
できました
球の表面積
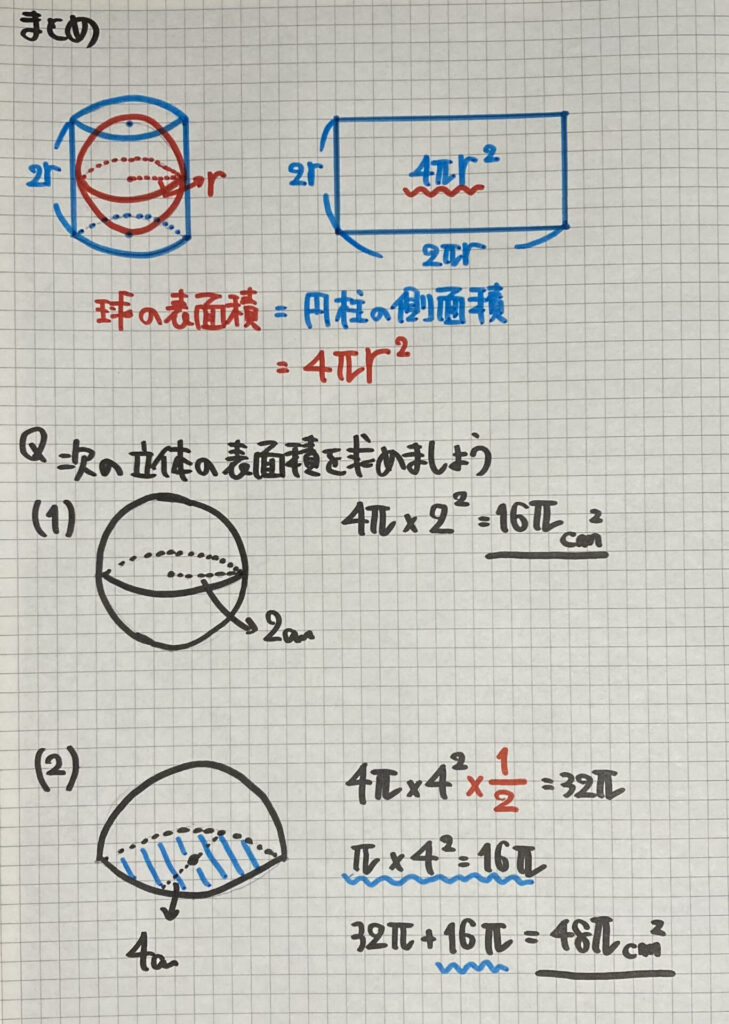
「球の表面積」は
「球」がきっちり入る
「円柱の側面積」と
同じになるという性質
があります
(詳しくは高校数学です…)
これは
このまま覚えてください
となります
(1)は
この公式を使うと
簡単に求めることができます
(2)は
「半円」なので
球の表面積×$\frac{1}{2}$を
しますね
そして底にある
「円の面積」を
忘れず足してくださいね
回転体の表面積
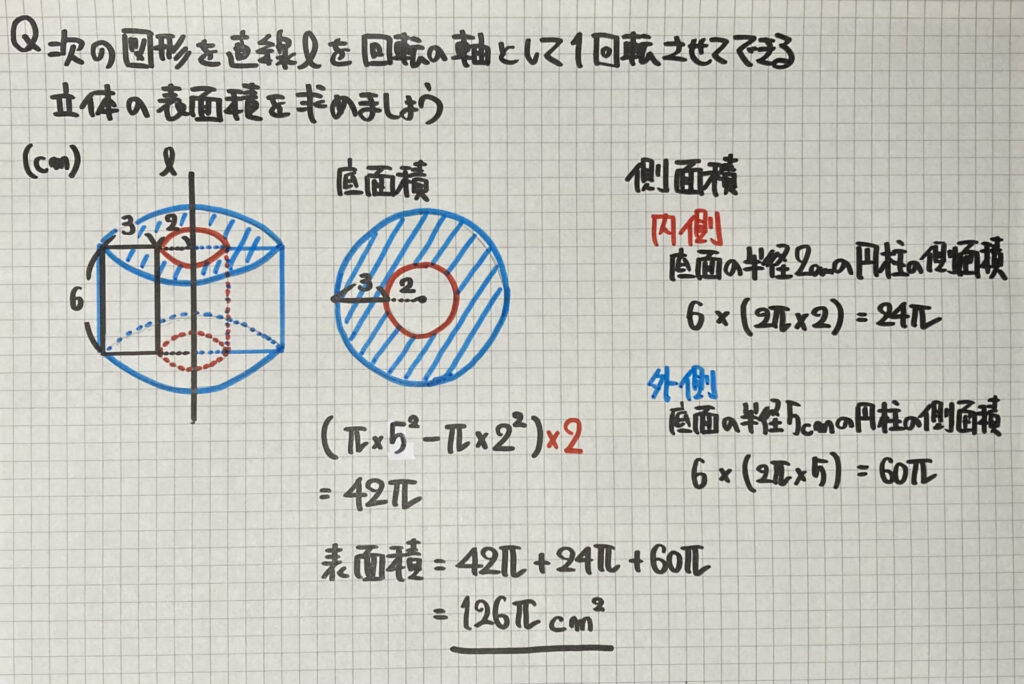
この問題で
間違えやすいのは
この部分
(底面の半径2cmの
円柱の側面積)を
足すことを
忘れないように
気をつけてください
立体の表面積のまとめ

・表面積
図形の表面の面積のこと
・展開図
立体を切り開いた図のこと
・柱体の表面積
底面積×2+側面積
(側面積=柱体の高さ×底面の周りの長さ)
・角錐の表面積
底面積+側面積
(側面積=合同な二等辺三角形×4)
・円錐の側面のおうぎ形の中心角
$360×\frac{半径}{母線}$
・円錐の表面積
底面積+側面積
(底面積=$π$×$半径^2$)
(側面積=母線×$π$×半径)
・球の表面積
(球の半径をrとすると)
$4πr^2$
以上、「数学嫌いな人が、
数学を楽しく好きになって欲しい」
かずのかずぶろぐでした