今回は
「いろいろな立体」を
やっていきます
「算数」でも立体は
学習しましたね
かずのかず
算数の
「立体」はこちらで
確認してくださいね
【小5算数】「角柱と円柱」の問題 どこよりも簡単な解き方・求め方角柱と円柱の性質について見ていきましょう ・角柱の名前は「底面」の形で決まる 「底面」が2つ(上下)にある 「側面」は「長方形」である・円柱の「側面」は「曲面(きょくめん)」と言い「平面」ではない 「側面の長方形の横の長さ」は「底面の円周」と等しくなる...
「算数」では
「柱体(ちゅうたい)」と言われる
「柱」の立体だけでしたが
「数学」では
「ピラミッド」のような
とがっている立体が出てきます
これを
「錐体(すいたい)」と
言います
「錐(すい)」の漢字
気をつけてくださいね
では、一緒にやっていきましょう
多面体
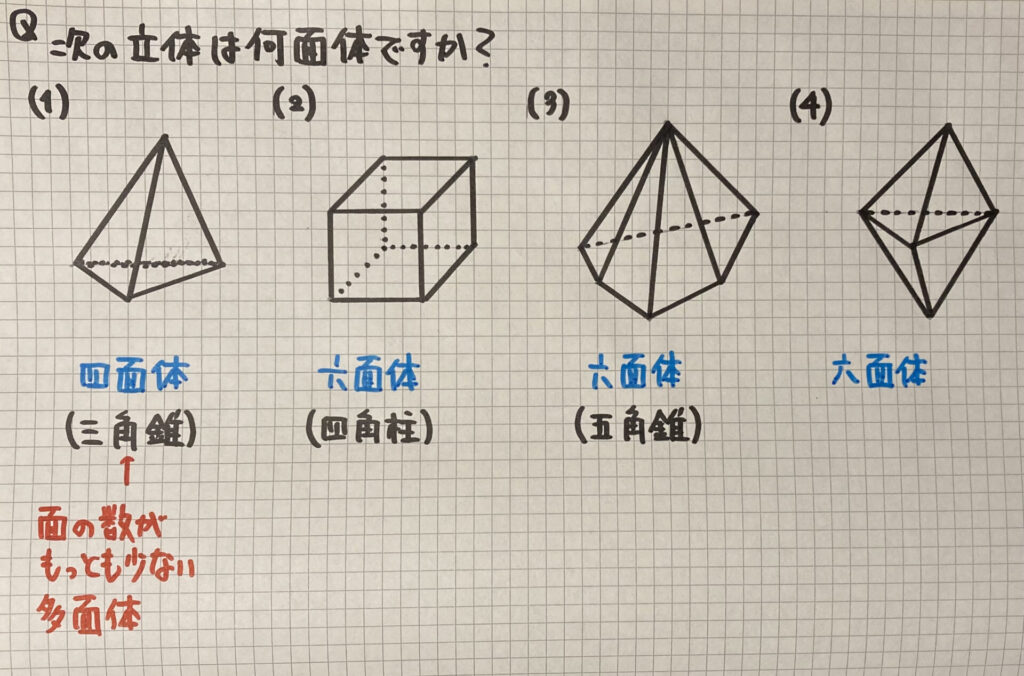
次は、立体の
「面の数」に注目した考え方
「多面体(ためんたい)」です
(2)(3)(4)は
「形」は全て違いますが
「面」に注目すると
全て「六面体」と表します
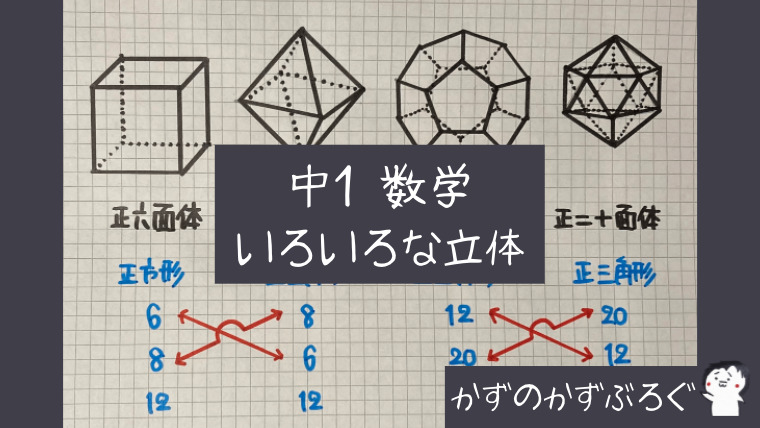
正多面体
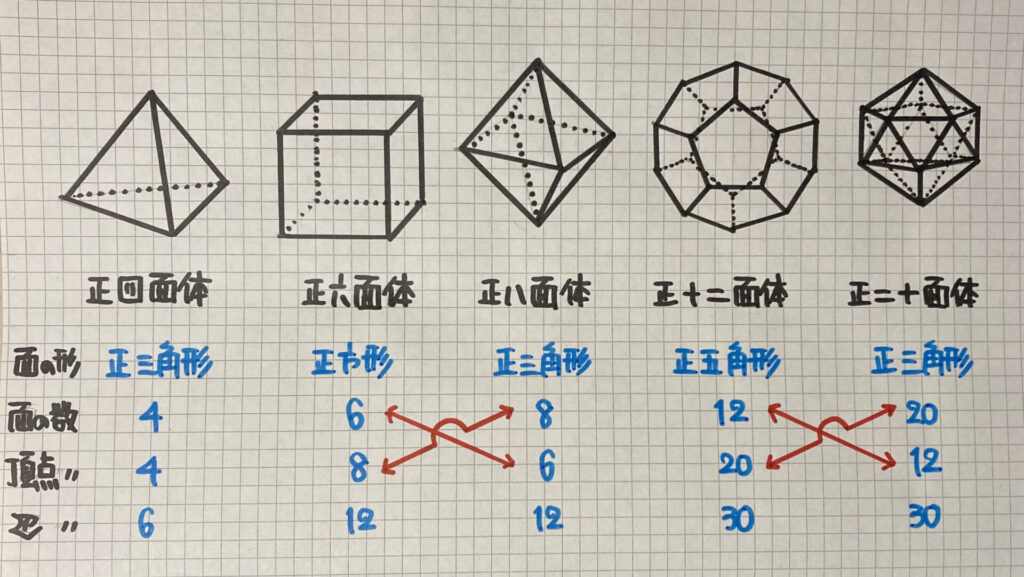
先ほど学習した
「多面体」ですが
「正多面体」と言われる
特別な「5種類」の
多面体があります
ノートの「青字」で書いた
「面の形」や「数」は
テストに出ることがあるので
テスト前には
しっかり確認しましょう
「赤字」の矢印に
注目しましょう
実は、この5種類の
「正多面体」には
2つの対(ペアー)があります
「正六面体と正八面体」
「正十二面体と正二十面体」です
と言いますが
「高校数学」の範囲です…
言葉を覚える必要は
ありませんので
安心してくださいね
ただ、「対(ペアー)になっている」
ことは覚えておくと
便利です
投影図(立面図と平面図)

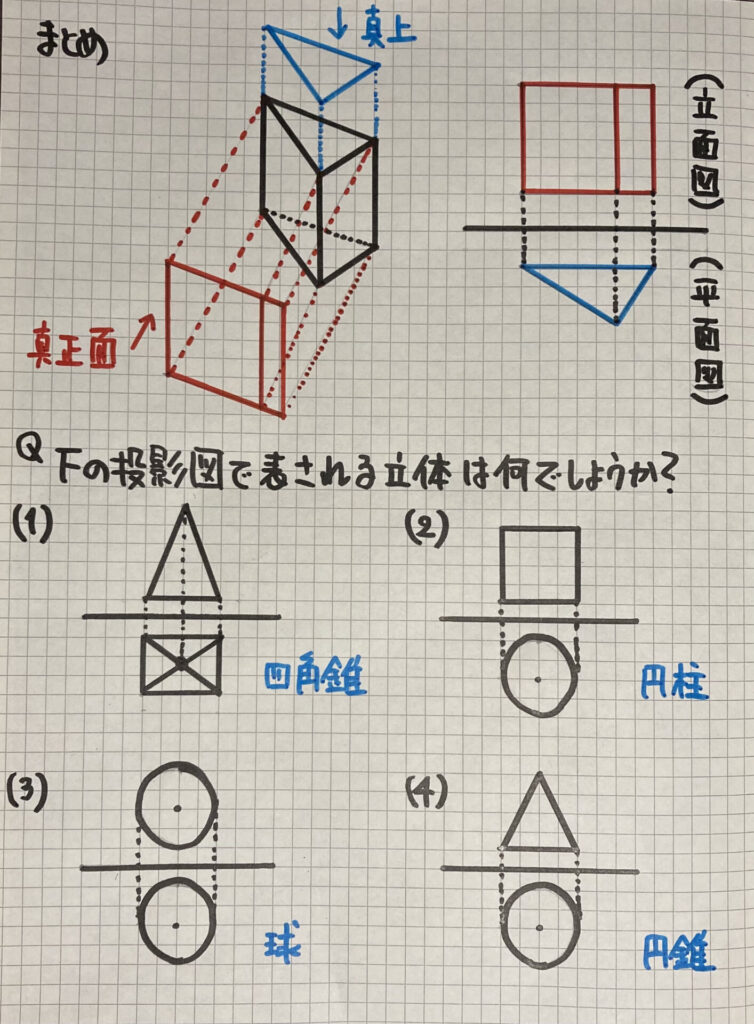
ここでは
新しい図形の見方
を学習します
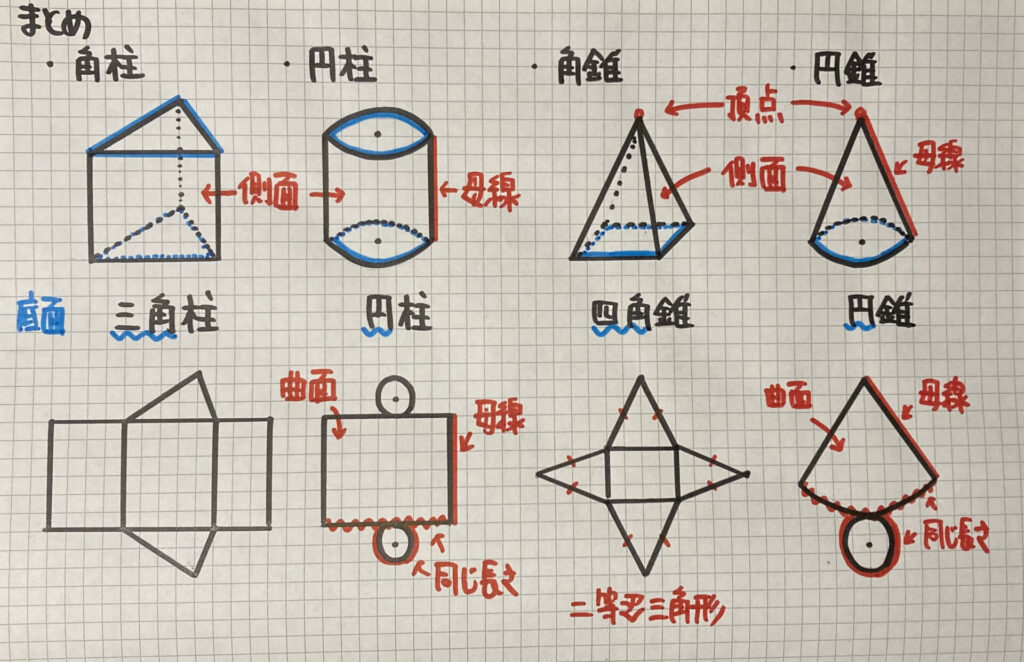
いろいろな立体のまとめ

・柱体(角柱・円柱)
- 底面積が2つ
- 側面は長方形
- 円柱の側面…曲面
・錐体(角錐・円錐)
- 底面積が1つ(頂点がある)
- 角錐の側面…二等辺三角形
- 円錐の側面…おうぎ形(曲面)
・正多面体
- 全ての面が合同な正多角形
- 頂点に集まる面の数が等しい
- 凸多面体(どこも凹んでいない)
- 全部で「5種類」
・投影図
立面図(りつめんず)
立体図形を真正面から見た図
平面図(へいめんず)
立体図形を真上から見た図
2つをまとめて
「投影図(とうえいず)」といいます
(立面図)を「上」に
(平面図)を「下」に書きます
かずのかず
以上、「数学嫌いな人が、
数学を楽しく好きになって欲しい」
かずのかずぶろぐでした