【中1数学】「反比例の式とグラフ」の問題　どこよりも簡単な解き方・求め方

反比例の式

⑴底辺が「1」㎝の時、高さは「12」㎝ですね

→$x$が「1」の時$y$は「12」

同じようにして考えると

$x$が「2」の時$y$は「6」…ですね

⑵「反比例の式」覚えてますか？

「算数」では

$y＝整数÷x$としていましたが

「数学」では

練習問題（$x$と$y$の関係を式に表す）

では実際に問題をやっていきましょう

「比例定数」は

$y=\frac{a}{x}$に代入しても

求めることができますが

⑵のように$x$や$y$が

「分数」の時は

計算を間違えやすいので

注意しましょうね

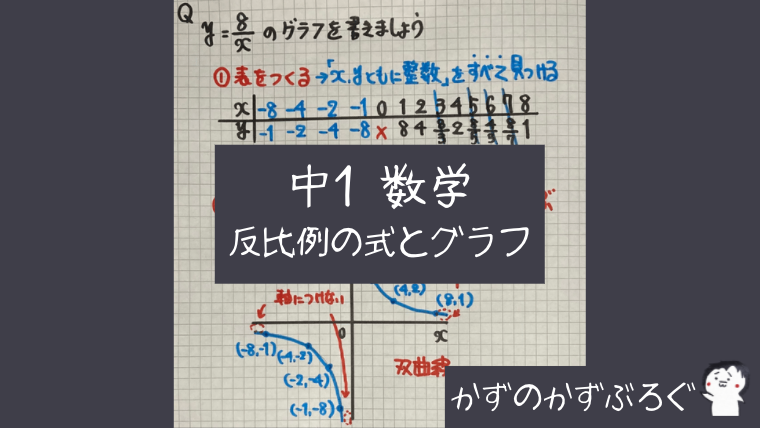
反比例のグラフ

まずは「反比例のグラフ」の書き方です

次に「反比例のグラフ」の特ちょうです

練習問題（グラフの書き方・式の求め方）

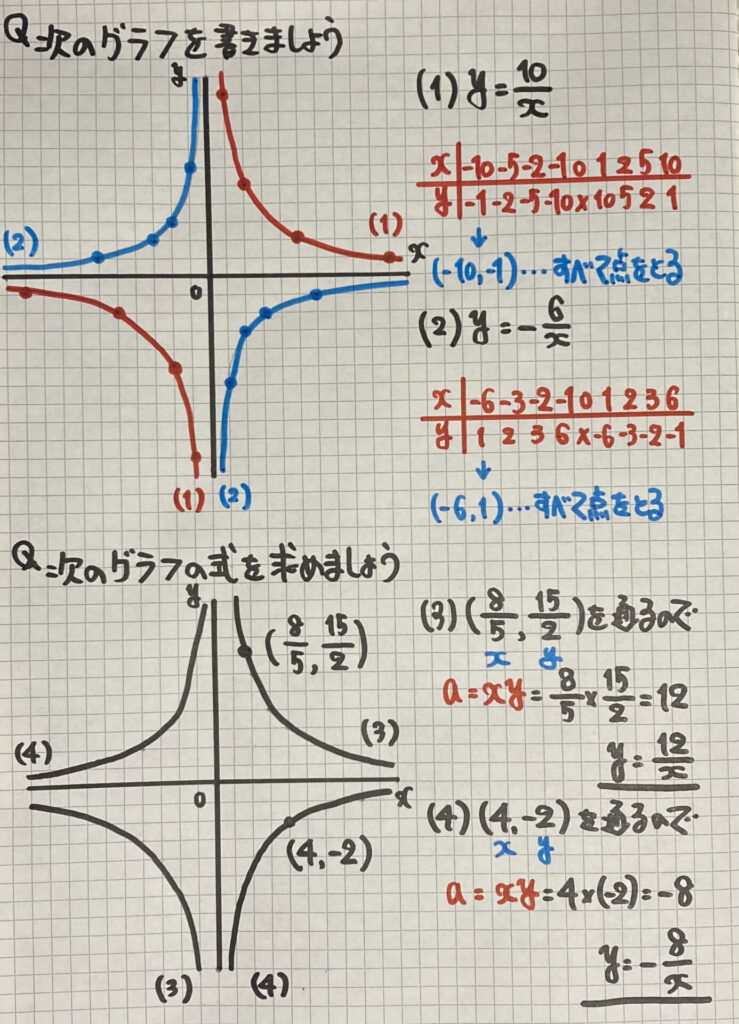
⑴⑵は$x$と$y$が

どちらも「整数」を

すべて見つけましょう

「負の数」を

忘れないように注意です

⑶⑷は

「グラフから式を求める」問題です

点の$x$座標$y$座標を

$a=xy$の$x$と$y$に

それぞれ代入して

$a$を求めましょう

⑶のように

座標が「分数」の時も

簡単に求めることができますね

反比例の式とグラフのまとめ

・反比例の式の求め方

$y＝a÷x＝\frac{a}{x}$

$a$は「比例定数」

$a=xy=x×y$で

求めることができる

・反比例の式の問題の解き方

1. 「$y$は$x$に反比例し〜」→$a＝xy$を用意
2. $x$と$y$を「代入」して$a$を求める

・反比例のグラフの書き方

1. $x$と$y$の表を作る
2. 整数の$x$と$y$を【すべて】見つける
3. グラフに、その点を【全部】とる
4. その点を通るなめらかな曲線で結ぶ

・反比例のグラフの特徴

原点を通らない

双曲線（そうきょくせん）になる

$a$（比例定数）が

$a$＞0（正の数）の時

「右上」と「左下」

$a$＜0（負の数）の時

「左上」と「右下」

かずのかず

以上、「数学嫌いな人が、

数学を楽しく好きになって欲しい」

かずのかずぶろぐでした