上から見ると丸いケーキを
みんなで食べるときは上のように
切りますよね
算数では「丸」と言わず
「円」と言いますね
この切ったケーキを
上から見た形を「おうぎ形」と言います
ここでは
この「円」や「おうぎ形」の
面積を見ていきましょう
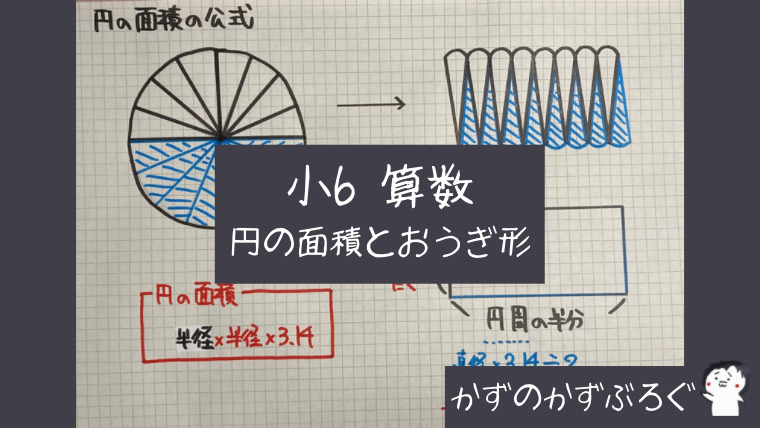
円の面積の公式
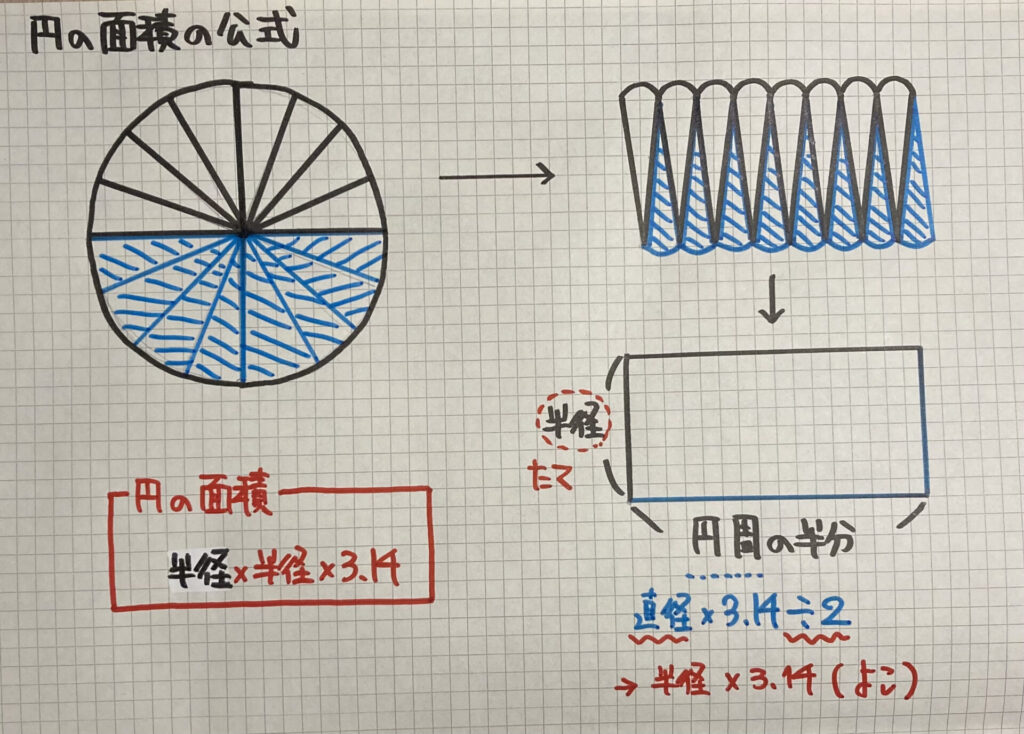
「円」を等分(同じ大きさに分ける)して
並べかえていくと
「四角形のように」なっていきます
ノートでは「円」を16等分していますが
これを、もっと細かく細かく…していって
並べかえると「ほとんど長方形」になります
算数では
「円の面積」を「長方形の面積」として
考えることにしています
この長方形の
「たて=円の半径」
「よこ=円周の半分(半径×3.14)」なので
長方形の面積 = たて × よこ
円の面積 = 円の半径 × 円周の半分
= 半径 × 半径 × 3.14
これが「円の面積」の公式です
練習問題
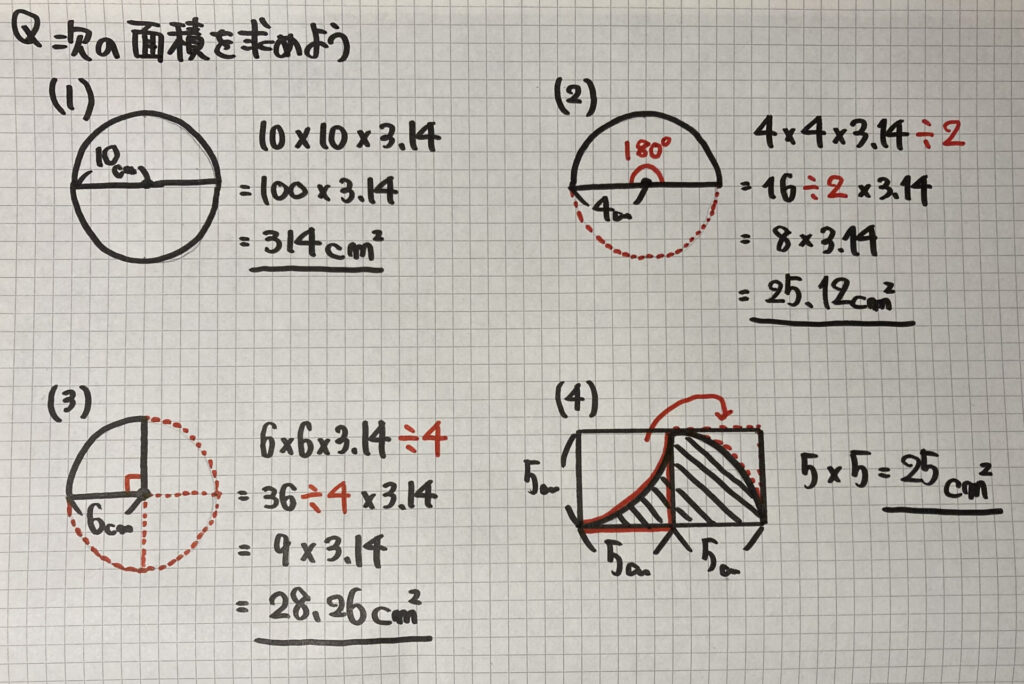
⑴は「円の公式」を使っています
⑵の図形は「半円」なので、
公式の後に「÷2」で半分にしています
⑶の図形は
「円を4等分した おうぎ形」なので
公式の後に「÷4」で求めています
⑷は求める図形の左側を移動すると
求める面積は「1辺5cmの正方形」になります
おうぎ形の面積
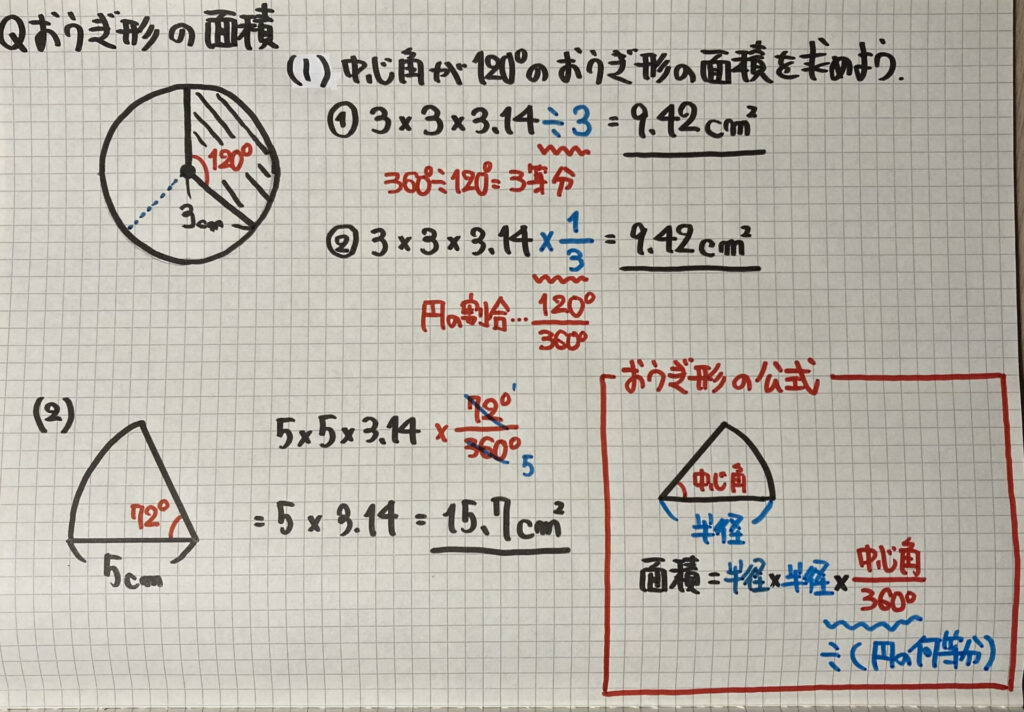
おうぎ形の面積の求め方は「2つ」あります
- 円の何等分かを求める
- 分数で円のどれだけ(割合)かを求める
「円の何等分かを求める」方法は
360°÷中心角から
そのおうぎ形が「円の何等分」かを求めて
「円の面積」÷「何等分」で
「おうぎ形の面積」を求めます
「分数で円のどれだけ(割合)かを求める」方法は
$\frac{中心角}{360°}$で円のどれだけかを求めます 「円の面積」×$\frac{中心角}{360°}$で「おうぎ形の面積」を求めます
360°÷「中心角」→「わりきれない」ことがあるので
②の方法をこれから使っていきましょう
おうぎ形の弧(こ)の長さ
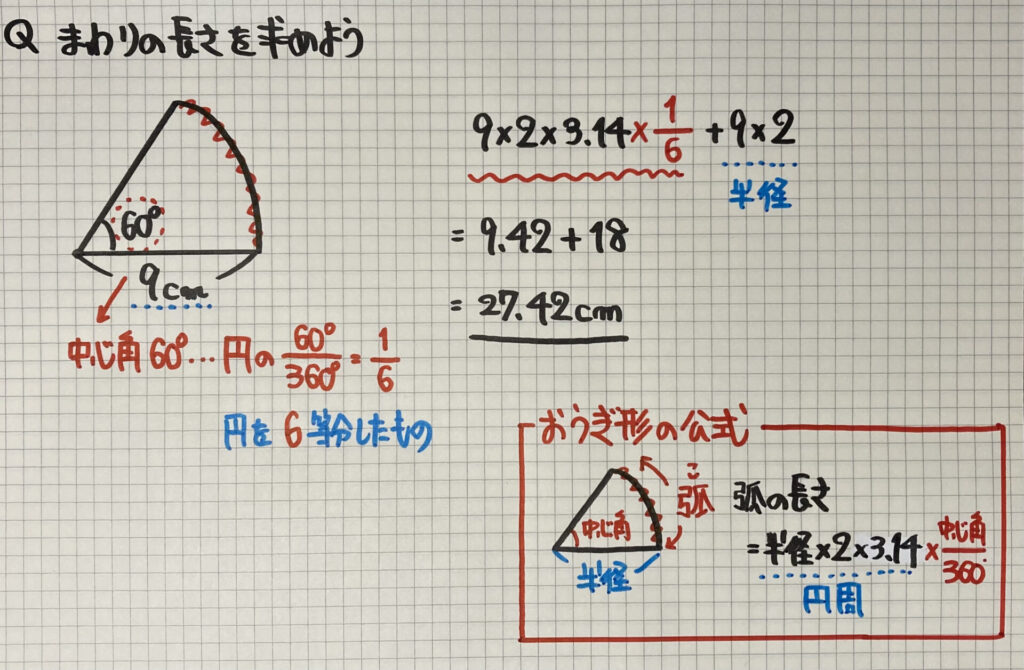
おうぎ形の曲線の部分を
「弧(こ)」と言います
で求めることができます
「まわりの長さ」を求める時は
「半径」を足すことを忘れないように
気をつけましょう
「円周」については
こちらで確認してくださいね
円を含む図形の面積①
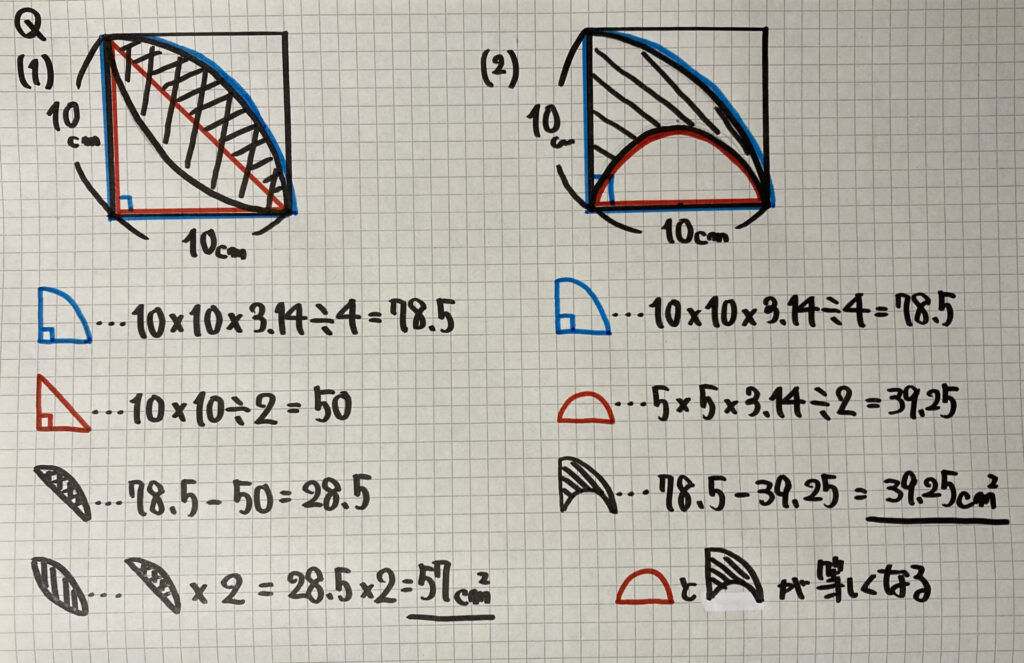
⑴は
- おうぎ形の面積を求める
- 直角三角形の面積を求める
- おうぎ形ー三角形=斜線の半分
- 斜線の半分×2 で求めましょう
⑵は
- おうぎ形の面積を求める
- 半円の面積を求める
- おうぎ形ー半円=斜線の面積 で求めましょう
ちなみに、どんな大きさになっても
「半円の面積」=「斜線部分の面積」
になります
円を含む図形の面積②
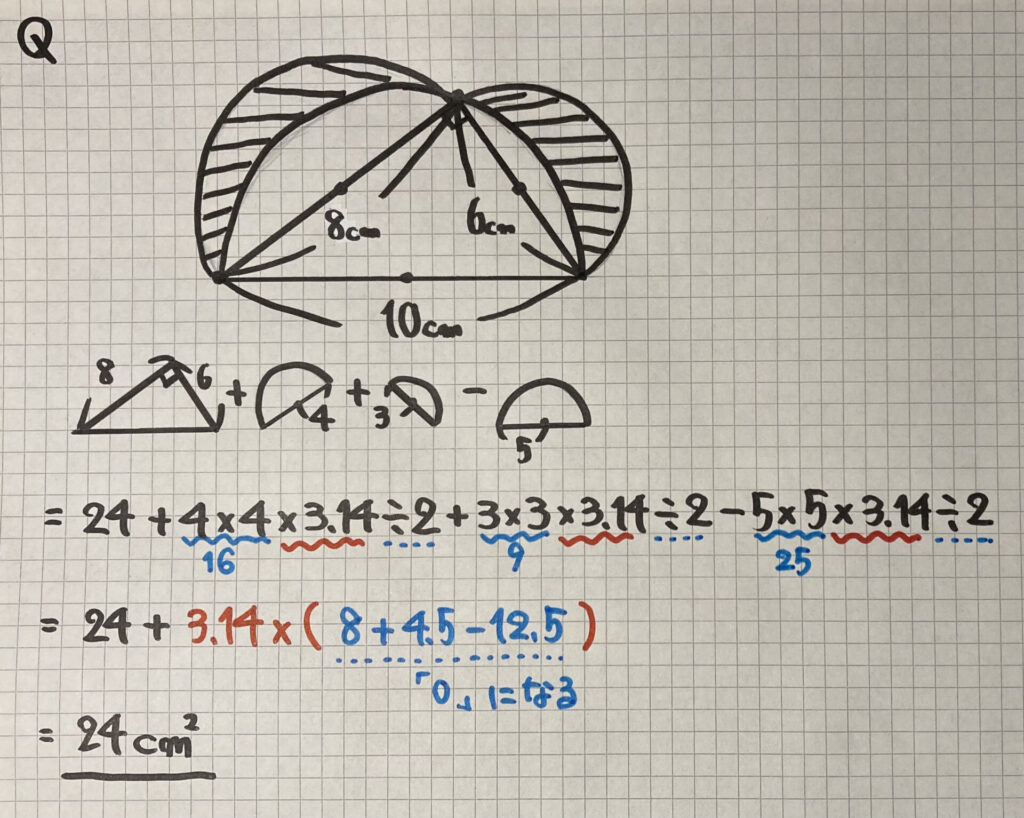
さあ、最後に有名な
「円を含む図形の面積」の問題です
「中1数学の定期テスト」に出ることがあります
見た目より、簡単な問題なので
しっかりノートを見てくださいね
求め方はノートにあるのですが
最後に「計算のくふう」をしています
- 「かけ算」と「わり算」の順番を入れかえる
- 3.14をまとめる(「分配法則」と言います)
「計算のくふう」については

こちらで確認してくださいね
すると「3.14×0=0」なので
斜線部分の面積=直角三角形の面積
となります。
知っていれば、すぐに答えが出せますよ
円の面積のまとめ

・円の面積=半径×半径×3.14
・おうぎ形の
面積=半径×半径×3.14×$\frac{中心角}{360°}$
弧の長さ=円周×$\frac{中心角}{360°}$
以上、「算数嫌いな人が、
算数を楽しく好きになって欲しい」
かずのかずぶろぐでした