【小6算数】「対称な図形」の問題　どこよりも簡単な解き方・求め方

算数には、三角形や四角形など、いろんな図形が出てきます

例えば、左右の形や大きさが同じ

上と下をひっくり返しても同じ

図形があります

ここでは、

• 「線対称（せんたいしょう）な図形」
• 「点対称（てんたいしょう）な図形」

という、2つのグループの図形について見ていきましょう

こちらの図形を見てください

左の辺と右の辺の長さが等しい

「二等辺三角形」ですね

「真ん中で2つに折ると、ぴったり重なります」

このような図形を「線対称」な図形と言います

次は、こちらの図形です

向かい合う辺の長さが平行で等しい長さの

「平行四辺形」ですね

「真ん中を中心に180°回転させる

　（上と下を逆さまにする）とぴったり重なります」

このような図形を「点対称」な図形と言います

線対称な図形の性質

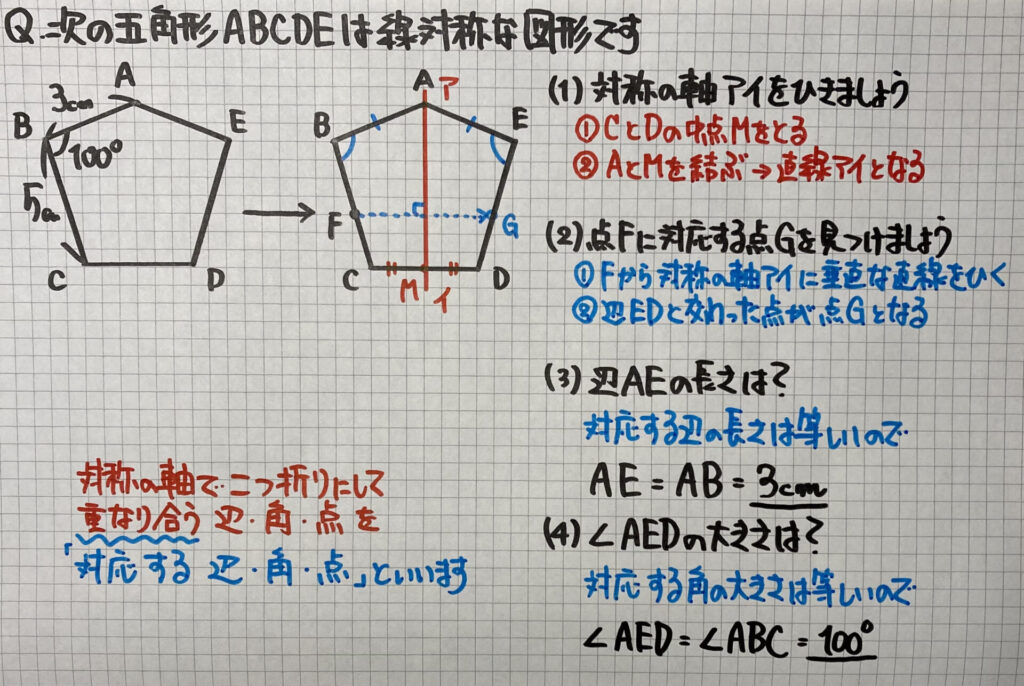
線対称な図形で

対称の軸で二つ折りにして

「重なり合う辺・角・点」を

「対応する　辺・角・点」といいます

書き方

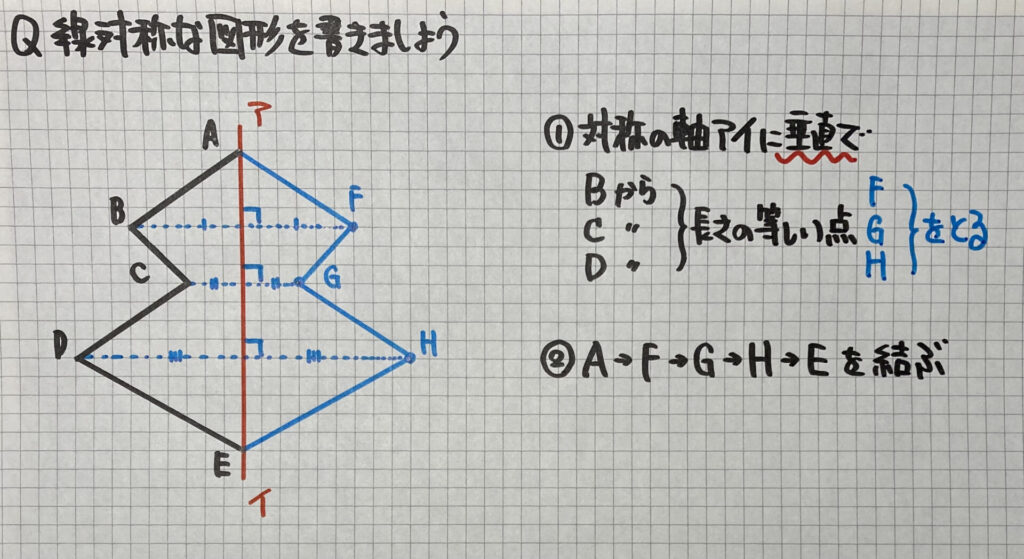
線対称な図形を書く時は

「対応する2つの点を結ぶ直線が

　対称の軸と垂直に交わる」ことに

気をつけましょう

点対称な図形の性質

点対称な図形で

対称の中心のまわりに180°回転したときに

「重なり合う辺・角・点」を

「対応する　辺・角・点」といいます

書き方

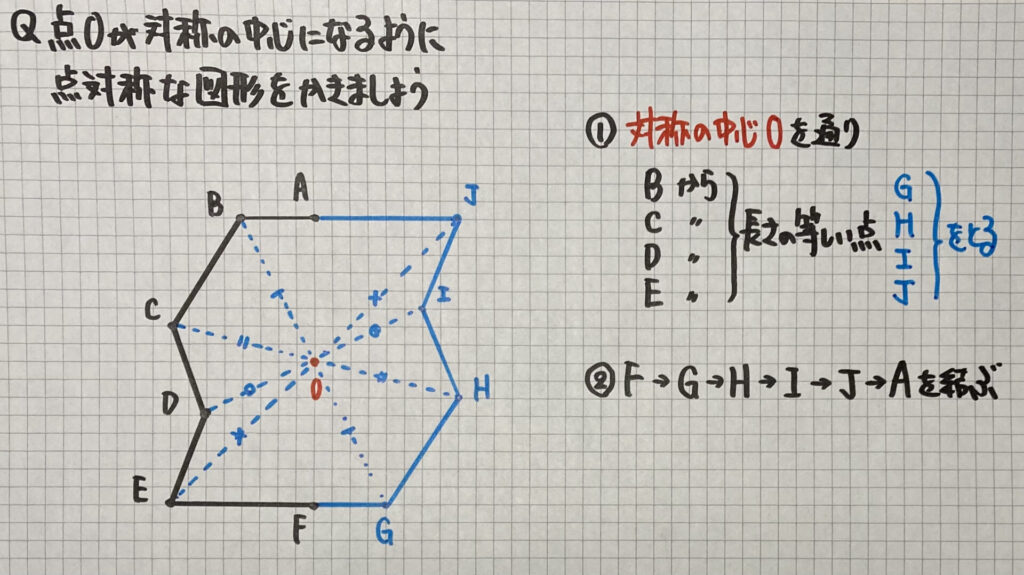
点対称な図形を書く時は

「対称の中心から、

　対応する2つの点までの長さ等しくなる」ことに

気をつけましょう

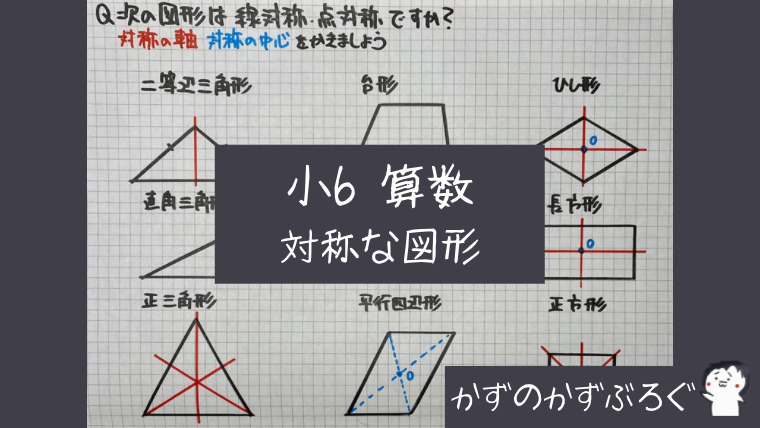
多角形と対称

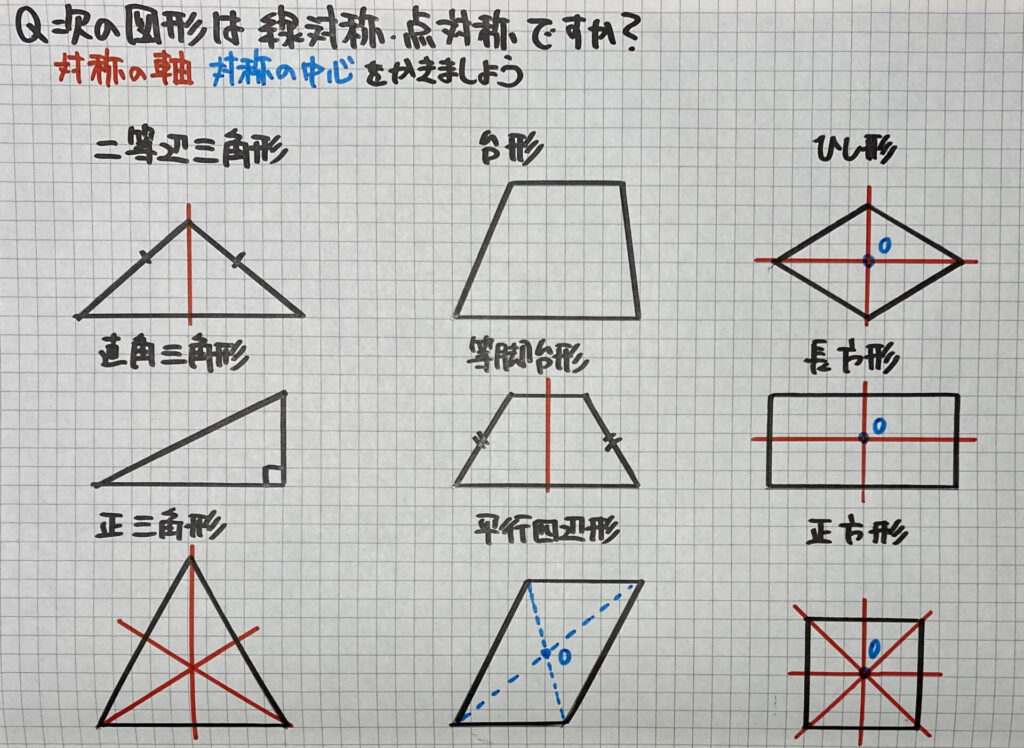
上の図形の特ちょうを表にまとめました

「赤線…対称の軸」「青点O…対称の中心」

図形	線対称な図形	対称の軸の本数	点対称な図形
二等辺三角形	○	1本	×
直角三角形	×	なし	×
正三角形	○	3本	×
台形	×	なし	×
等脚台形※	○	1本	×
平行四辺形	×	なし	○
ひし形	○	2本	○
長方形	○	2本	○
正方形	○	4本	○

正多角形と対称

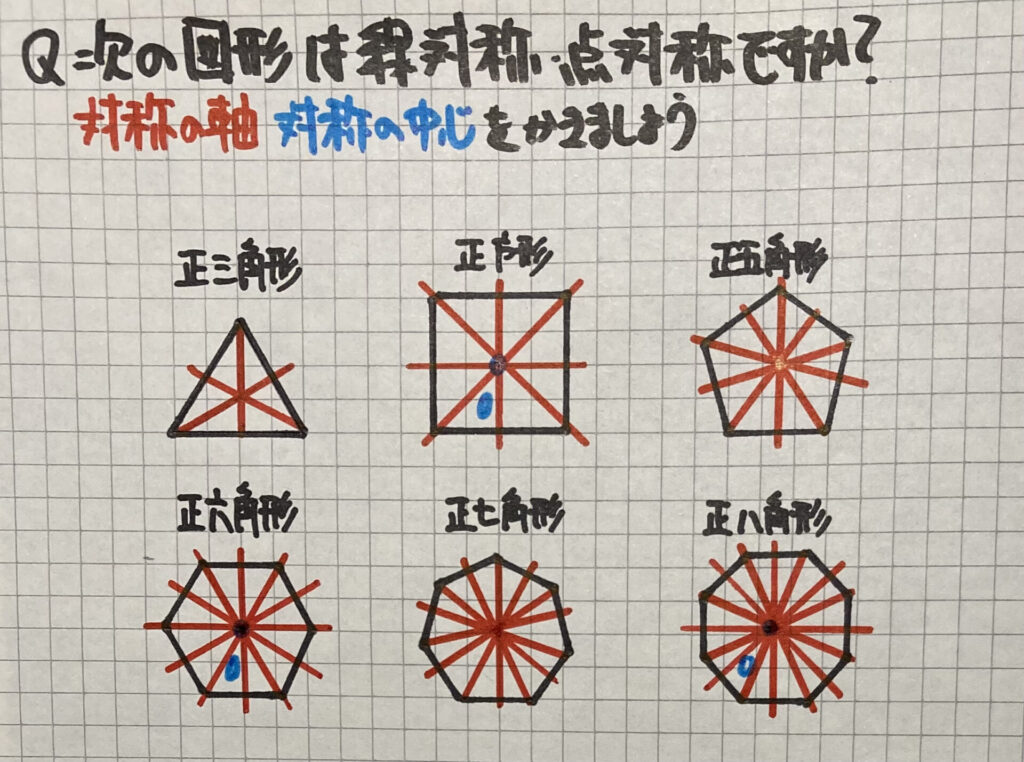
上の正多角形の特ちょうを表にまとめました

「赤線…対称の軸」「青点O…対称の中心」

多角形	線対称な図形	対称の軸の本数	点対称な図形
正三角形	○	3本	×
正方形	○	4本	○
正五角形	○	5本	×
正六角形	○	6本	○
正七角形	○	7本	×
正八角形	○	8本	○

対称な図形のまとめ