世の中には大切なものを守るのに
「鍵」や「パスワード」が
ありますね
上のような「番号を合わせる鍵」の
「番号の決め方」は何通りあるでしょうか
もし、番号が
「0」から「9」までとすると
全部で、「6561通り」あります
ということは…
「6561回」番号を試すと
このような鍵を開けることが
できてしまいます…
鍵にはくれぐれも
気をつけましょうね
では「算数」の話に戻りましょう
さっきの「6561通り」ですが
実は、数の「並べ方」という考え方を
使っています
式で表すと
「0」から「9」まで
並べ方は「9通り」なので
「9×9×9×9=6561通り」
となります
では、この「並べ方」と
もう1つ似ている
「組合せ方」について
一緒に見ていきましょう
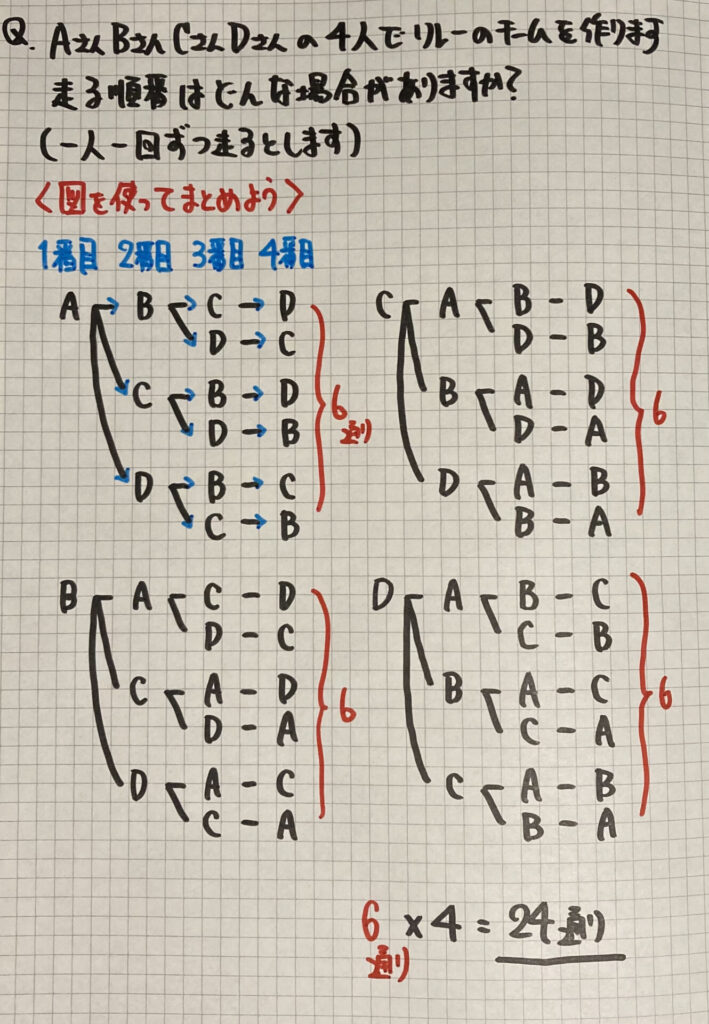
左から「1番目」…「4番目」の人が
並んでいると考えましょう
左上の図を見てください
このように考えましょう↓
「1番目」が「Aさん」のとき
「2番目」は「Bさん」「Cさん」「Dさん」
の「3通り」あります
→「Aさん」から「3本」の線(矢印)がのびています
「1番目」が「Aさん」
「2番目」が「Bさん」のとき
「3番目」は「Cさん」「Dさん」
の「2通り」あります
→「Bさん」から「2本」の線(矢印)がのびています
「1番目」が「Aさん」
「2番目」が「Bさん」のとき
「3番目」が「Cさん」のとき
「4番目」は「Dさん」
の「1通り」あります
→「Cさん」から「1本」の線(矢印)がのびています
同じように
「1番目」が
「Bさん…6通り」
「Cさん…6通り」
「Dさん…6通り」になるので
全部で「24通り」となります
このように図を書いていくと
「数え忘れ」がなくなるので
きちんと「すべての場合」の「並べ方」を
求めることができます
(自分で書くときは
「矢印」でなく「直線」で書こうね)
練習問題
整数を作る
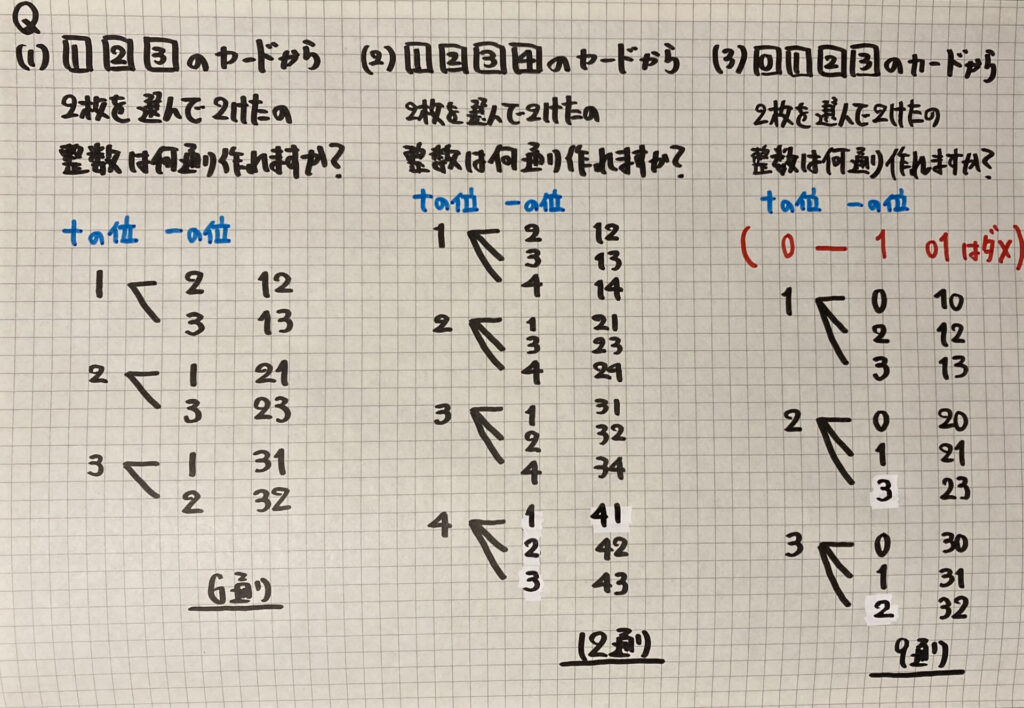
⑵と⑶は
どちらも「4枚」のカードを
使うのですが
「0が入っているとき」は
気をつけましょう
「十の位」の「0」
→「01」は「2けたの整数」なりません
コインを投げる
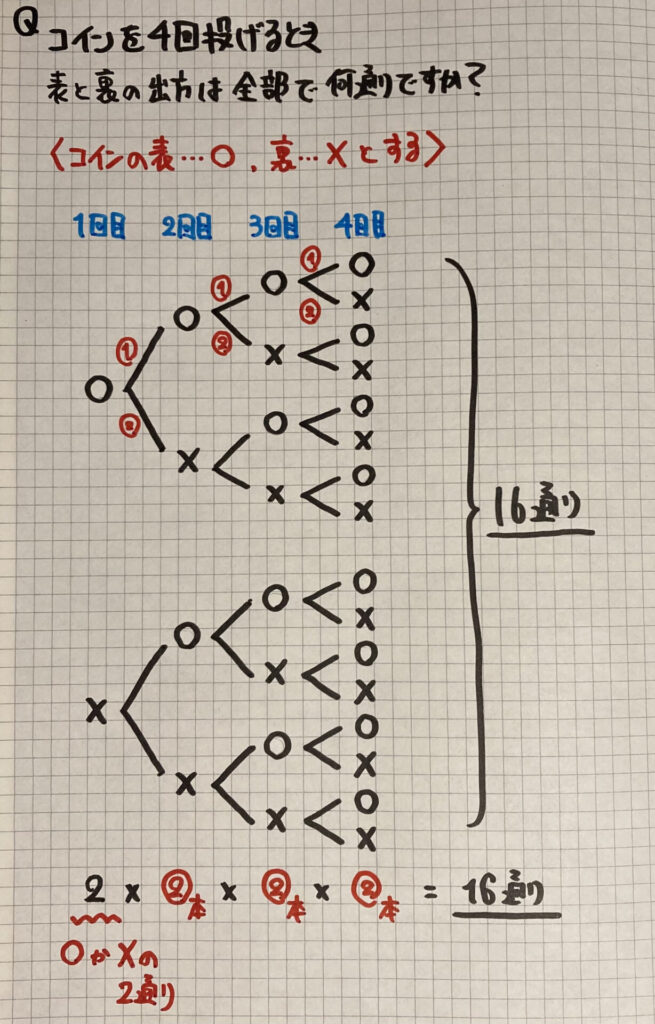
1回目から4回目までを
図に表しました
一番下に式を書いています
図からも分かるように
「コインの出方」は
「表」か「裏」かの「2通り」です
そこから「2本」ずつ「直線」が
出ていますね
これを式で表すと
「2×2×2×2=16通り」
と求めることができます
組合せ方
「並べ方」とよく似ているのですが
ここからは「組合せ方」について
見ていきましょう
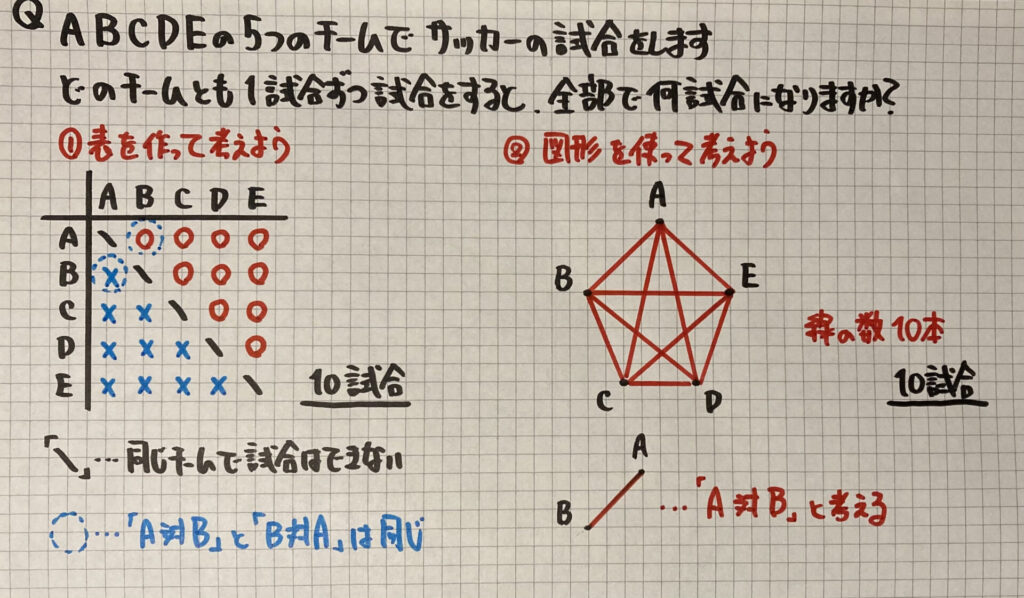
「並べ方」と違って
求め方は
①表を作って
②図形を使って
求めることができます
分かりやすい方で
やってみてくださいね
練習問題
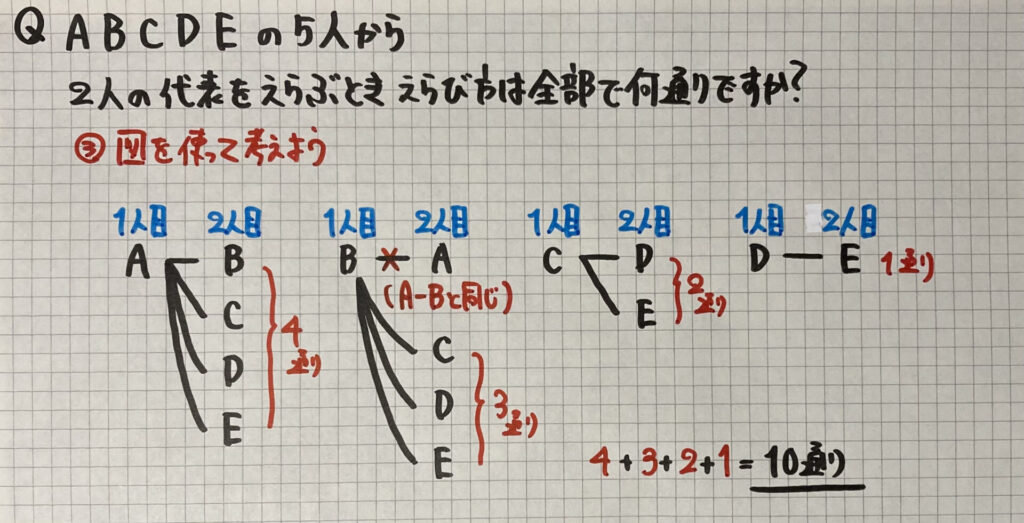
「組合せ方」と同じような
「直線を使った図」でも
求めることができます
ここで気をつけるのは
さっきの問題と同じように
そうすると
「1番目」が
「A…4通り」
「B…3通り」
「C…2通り」
「D…1通り」になるので
全部で「10通り」となります
並べ方と組合せ方のまとめ

・「並べ方」は
- 直線で結ぶ図
・「組合せ方」は
- 直線で結ぶ図
- 表を作る
- 図形を使う
で求めましょう
慣れてきたら
図を一部書いてから
「計算で求める」ことも
できるようになりますよ
「頭の中で数える」
「バラバラな順番で書いていく」と
「数え忘れてしまう」ことが
あるので気をつけましょう
以上、「算数嫌いな人が、
算数を楽しく好きになって欲しい」
かずのかずぶろぐでした