前回は
「円周角と中心角」
について学習しました

【中3数学】「円周角と中心角」の問題 どこよりも簡単な解き方・求め方今回から「円の性質」について学習していきます まずは新しい「円周角」という言葉「中心角」や「弧」との関係を理解していきましょう...
今回は
前回学習した
「円周角の定理の」
「逆」と「円の性質の利用」
について一緒に
見ていきましょう
円周角の定理の逆
- 円周上に3点A,B,Cがあって、点Pが、直線ABについて点Cと同じ側にあるとき、$\angle APB=\angle ACB$ならば、点Pはこの円の$\stackrel{\huge\frown}{ACB}$上にある。
- 2点C,Pが、直線ABについて同じ側にあるとき、$\angle APB=\angle ACB$ならば、4点A,B,C,Pは同じ円周上にある。
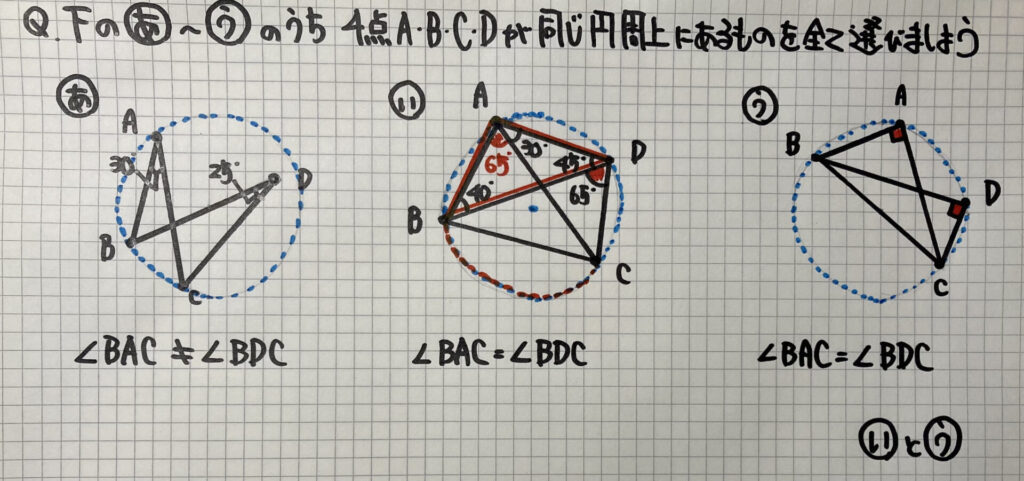
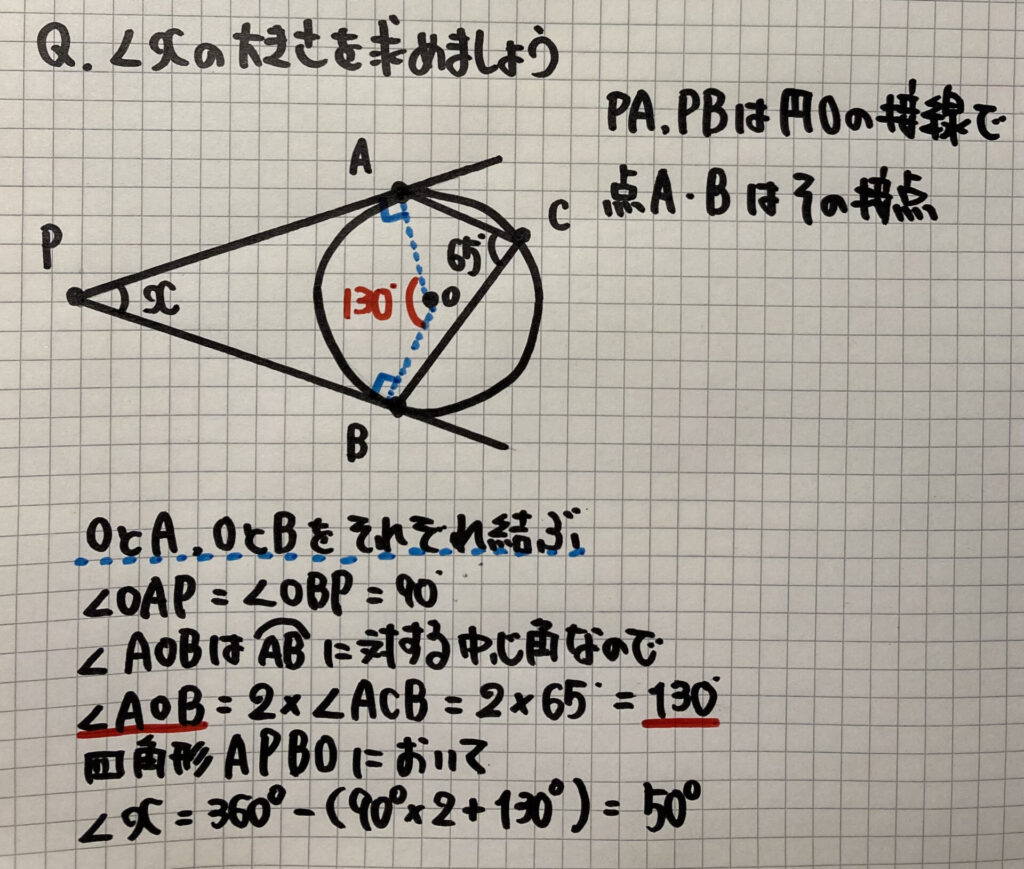
練習問題

「円周角の定理の逆」
を使って考えていきましょう
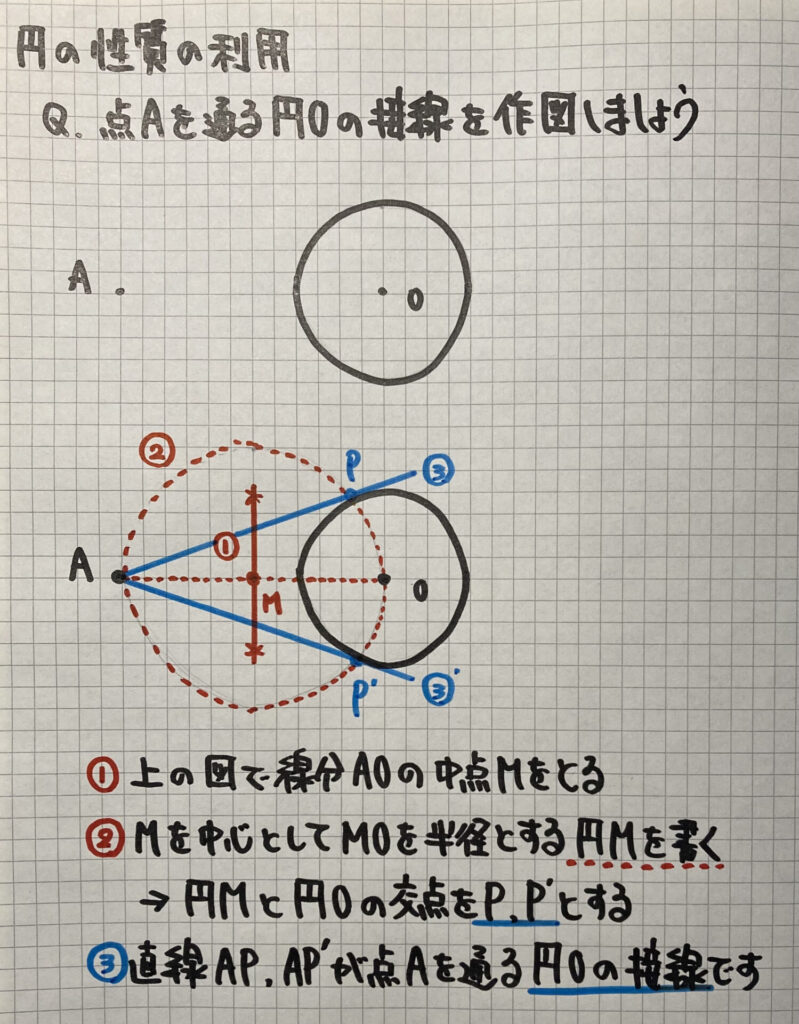
円の性質の利用
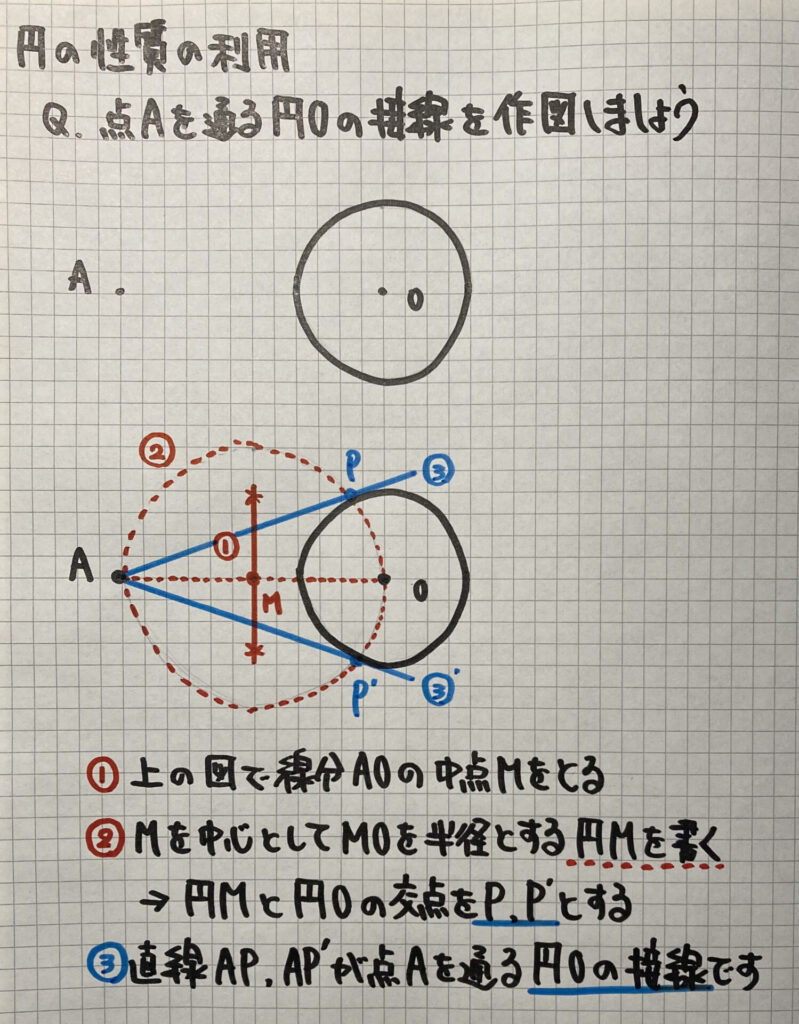
接線の作図
「円の性質」を使って
「円外の1点Aを通る、円Oの接線の作図」
をやってみましょう
円と接線のまとめ
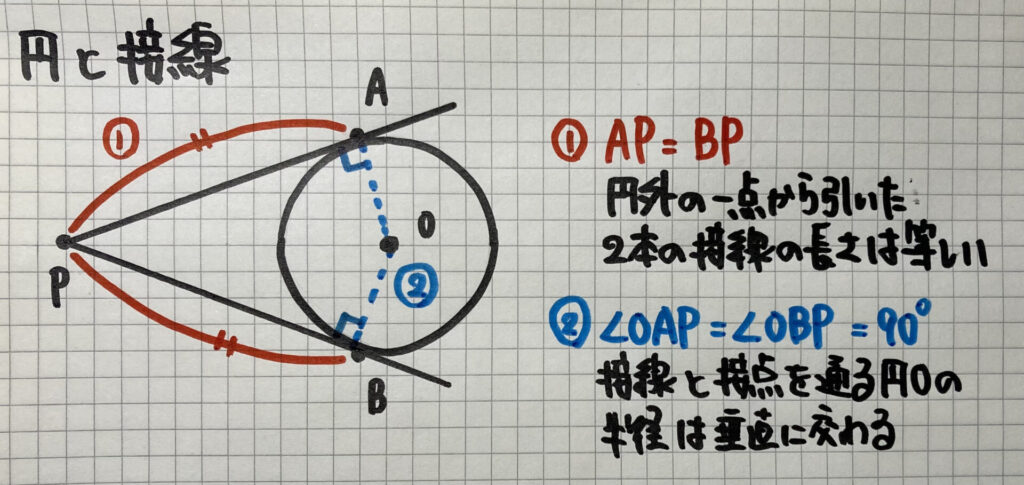
これから
いろんな図形の問題を解くのに
必要な考え方です
しっかり覚えておきましょう
練習問題

先ほど学習した
を使って解いていきます
円周角の定理の逆と円の性質の利用のまとめ

・円周角の定理の逆
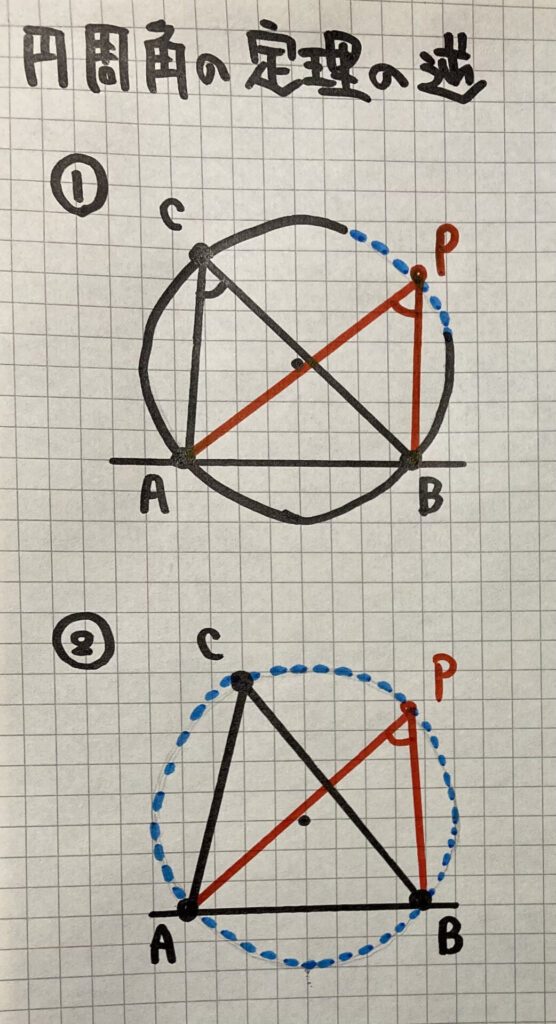
円周角の定理の逆
- 円周上に3点A,B,Cがあって、点Pが、直線ABについて点Cと同じ側にあるとき、$\angle APB=\angle ACB$ならば、点Pはこの円の$\stackrel{\huge\frown}{ACB}$上にある。
- 2点C,Pが、直線ABについて同じ側にあるとき、$\angle APB=\angle ACB$ならば、4点A,B,C,Pは同じ円周上にある。
・接線の作図
・円と接線のまとめ

以上、「数学嫌いな人が、
数学を楽しく好きになって欲しい」
かずのかずぶろぐでした