前回
「相似の証明」
を学習しました
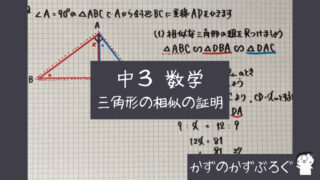
今回は
今まで学習した
「相似な図形」
を利用して
「平行線と線分の比」
について
一緒に
見ていきましょう
ピラミッド型・砂時計型
これから
図形の問題で
よく「相似」を
利用して
長さを求めるのですが
一番基本となる
「2つ」の型
「ピラミッド型」と
「砂時計型」と
言います
証明はノートで
確認してくださいね
2つの証明が
よく似ていることが
分かります
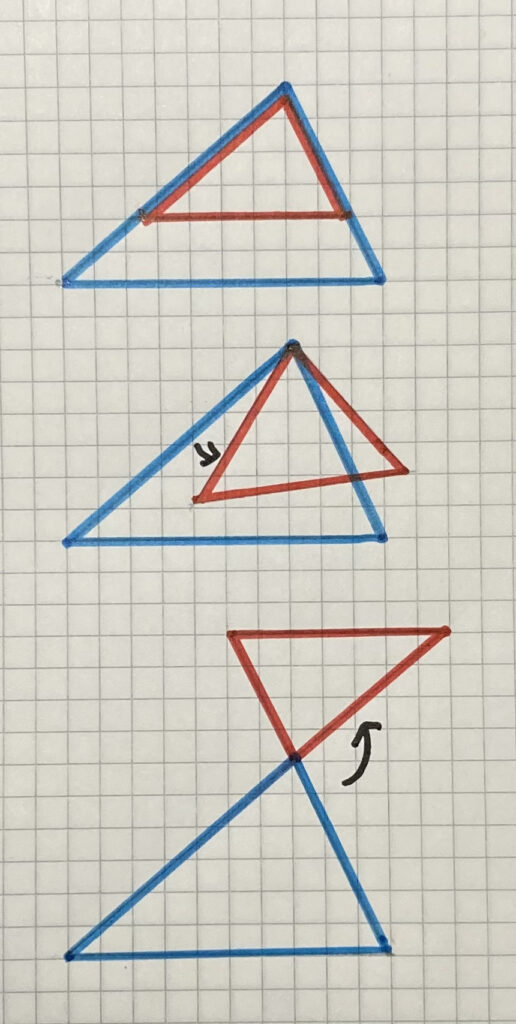
このように
「ピラミッド型」の△ADE
(赤の)小さな三角形が
移動して
「砂時計型」の△ADE
(赤の)上の三角形に
なったと考えると
同じ相似な三角形
であることが
分かりますね
ピラミッド型
DE//BCならば
- AD：AB＝AE：AC＝DE：BC
- AD：DB＝AE：EC
逆も言うことができます
AD：AB＝AE：ACならば
DE//BC
AD：DB＝AE：ECならば
DE//BC
位置は違いますが
「砂時計型」
も同じことが言えます
砂時計型
ED//BCならば
- AD：AB＝AE：AC＝ED：BC
逆も言うことができます
AD：AB＝AE：ACならば
ED//BC
練習問題
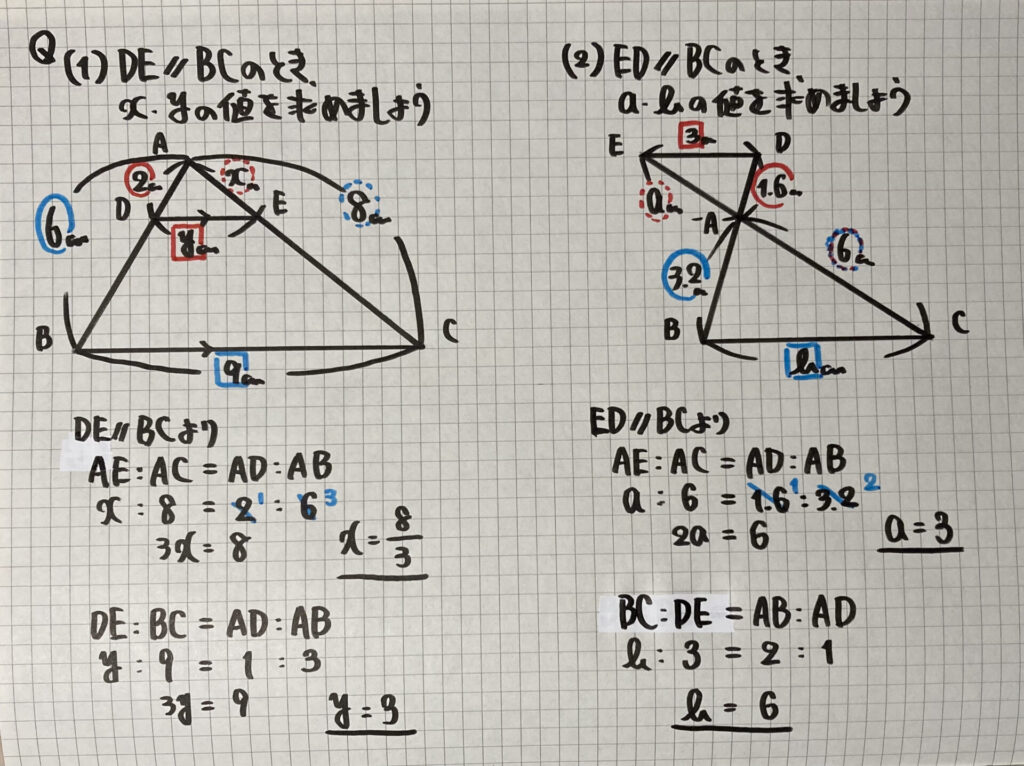
前回の
「相似の証明」から
「比例式」を作ったように
「平行線(相似)」
↓
「比例式」
↓
「線分の長さ」
を求めることができます
平行線にはさまれた線分の比
三角形でない
「平行線にはさまれた線分の比」
の関係です
ノートにまとめたように
「直線S」を
引くことによって
(平行四辺形を作り)
「相似」を見つける
ことができると思います
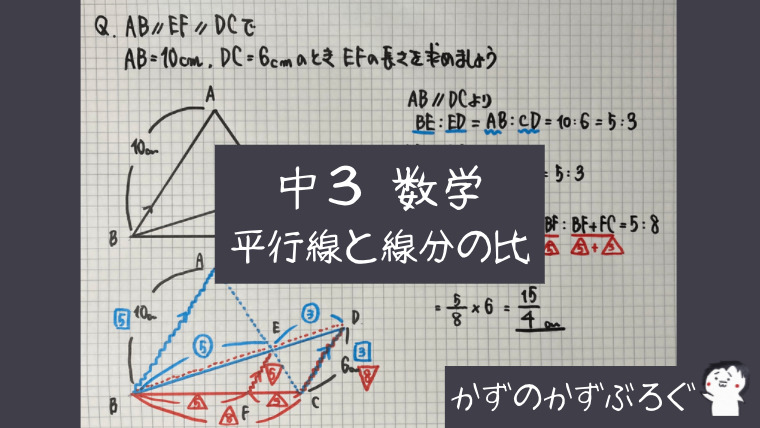
練習問題
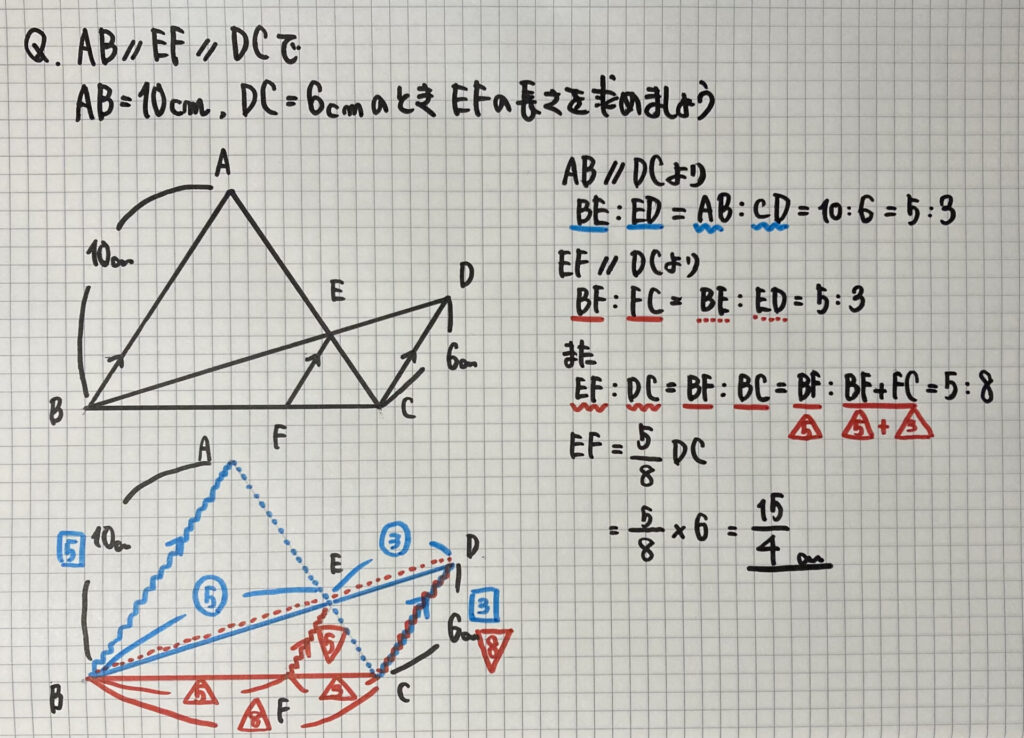
「平行線にはさまれた線分の比」
のとても有名な問題です
ノート以外の
解き方(やり方)
もありますので
是非、探してみてください
AB//DCより
- 横向きの「砂時計型」
- △AEB∽△CEDから
BE：ED＝AB：CD＝5：3
EF//DCより
- 横向きの「ピラミッド型」
- △BEF∽△BDCから
BF：FC＝BE：ED＝5：3なので
EF：DC＝BF：BC＝5：8
EF＝$\frac{5}{8}$DC＝$\frac{15}{4}$
となりますね
平行線と線分の比のまとめ
・平行線
- ピラミッド型
- 砂時計型 を探す
・ピラミッド型
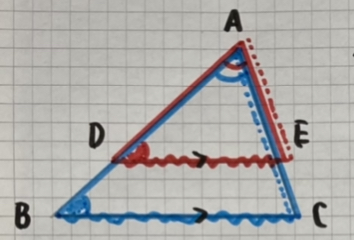
DE//BCならば
- AD：AB＝AE：AC＝DE：BC
- AD：DB＝AE：EC
AD：AB＝AE：ACならば
DE//BC
AD：DB＝AE：ECならば
DE//BC
・砂時計型
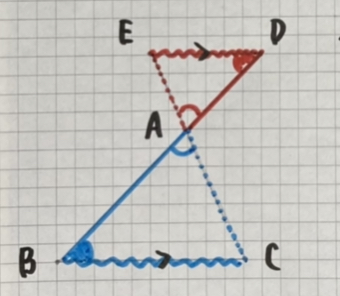
ED//BCならば
- AD：AB＝AE：AC＝ED：BC
AD：AB＝AE：ACならば
ED//BC
・平行線にはさまれた線分の比
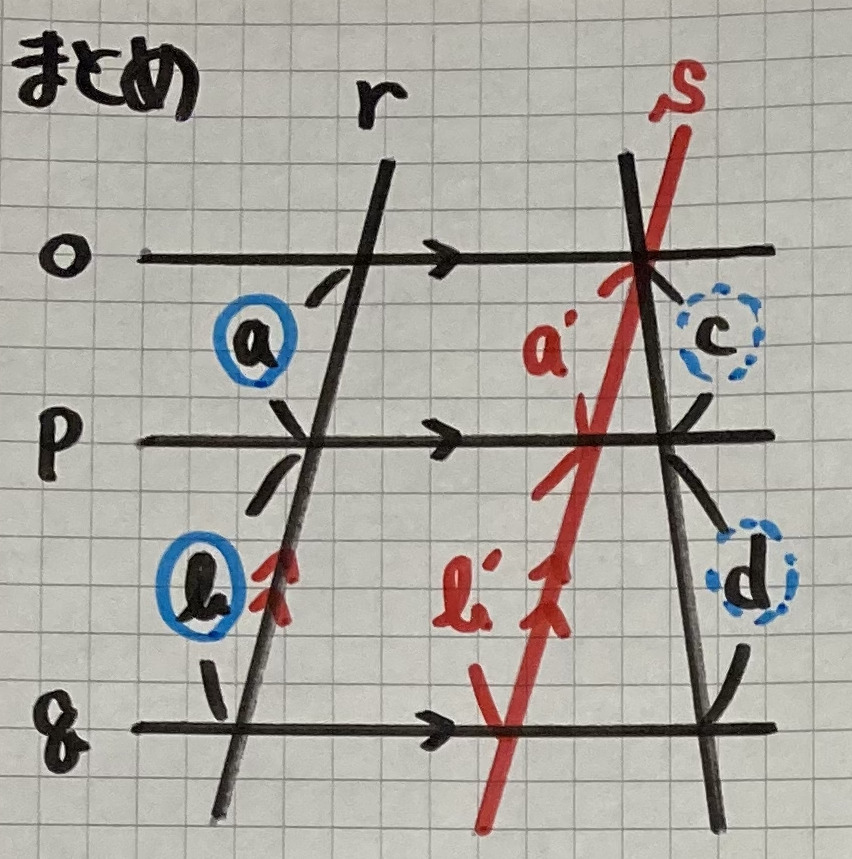
2つの直線が
3つの平行な直線と
交わっている時
- $a:b=c:d$
- $a:c=b:d$
以上、「数学嫌いな人が、
数学を楽しく好きになって欲しい」
かずのかずぶろぐでした
