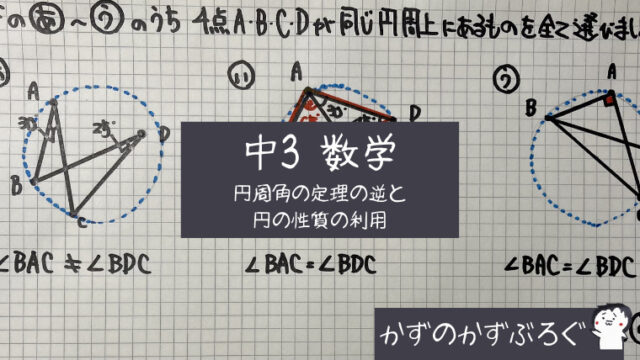
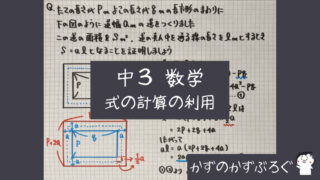
今回から
新しい単元
「$\sqrt{ ○ }$」
の学習です
電卓で見たことが
あるかもしれませんね
では一緒に
やっていきましょう
練習問題

よく間違える問題です
- ○の平方根→○の正負(±)の平方根「2つ」
- $\sqrt{ ○ }$=○の正の平方根「1つ」
- $−\sqrt{ ○ }$=○の負の平方根「1つ」
(4)0.25の平方根ですが
「±$\sqrt{ 0.25 }$」と
答えると間違いになります
(0.5×0.5=0.25なので)
(5)「分数の平方根」
の書き方には気をつけましょう
最後の問題は
「次の数を求めましょう」
とあるので
(1)$\sqrt{ 36 }$=±6と
答えると間違いになるので
気をつけてください
途中の式があると
間違えにくいと思います
慣れてくれば
「=$\sqrt{ 6^2 }$」
の部分は省略して
大丈夫です
平方根の大小

整数の「2」と「3」の
大小関係は
「2<3」です
では「$\sqrt{ 2 }$」と「$\sqrt{ 3 }$」の
大小関係は
どうなるでしょう
ノートのように
正方形の面積で
考えると
分かりやすいですね
(3)(4)のように
- 平方根の「負の方」
- −$\sqrt{ ○ }$
の時は注意です
「絶対値」だけを「2乗」しましょう
最後の問題は
「自然数$a$…」とあるので
「負の数」や「0」は入らないので
気をつけましょう
平方根のまとめ

・平方根の意味
$a$の平方根
2乗すると$a$になる数
「平方根」⇔「2乗する」
の関係です
平方根を表す記号
「√‾」を根号(こんごう)と言い
「ルート」と読みます
平方根は2つあります
- 正の平方根
- 負の平方根 です
・平方根の問題
- ○の平方根→○の正負(±)の平方根「2つ」
- $\sqrt{ ○ }$=○の正の平方根「1つ」
- $−\sqrt{ ○ }$=○の負の平方根「1つ」
・平方根の大小
正の数$a、b$について
$a<b$ならば$\sqrt{ a }<\sqrt{ b }$
かずのかず
以上、「数学嫌いな人が、
数学を楽しく好きになって欲しい」
かずのかずぶろぐでした