前回は
「二次方程式の利用①」
として
「$a$の値・もうひとつの解」
「整数」の問題
「割合」の問題を学習しました

【中3数学】「二次方程式の利用①($a$の値 整数 割合)」の問題 どこよりも簡単な解き方・求め方前回までで「二次方程式」の「計算」について学習しました 今回は「二次方程式」の「利用(文章題)」として「aの値・もうひとつの解」「整数問題」「割合の問題」を一緒に見ていきましょう...
今回は
「二次方程式の利用②(文章題)」
として
「道幅」「長方形」
「動点」「対角線」
の問題を一緒に
見ていきましょう
「長方形」の問題

長方形は
向かい合う
「たて」「よこ」の長さが
等しいので
を利用しましょう
この問題は
「たて」「よこ」の
区別がないので
方程式の解
「$x=12 , 15$」が
長方形のそれぞれの
辺の長さになります
「動点」の問題

動点の問題は
動いた分の長さ
を図形に書き込んで
問題を解きましょう
最後に
「解の吟味です」
点Qは「8秒」で
Cに到着するので
$t<8$より
$t=10−2\sqrt{ 10 }$
となり
答えは
$10−2\sqrt{ 10 }$秒後
です
「対角線」の問題
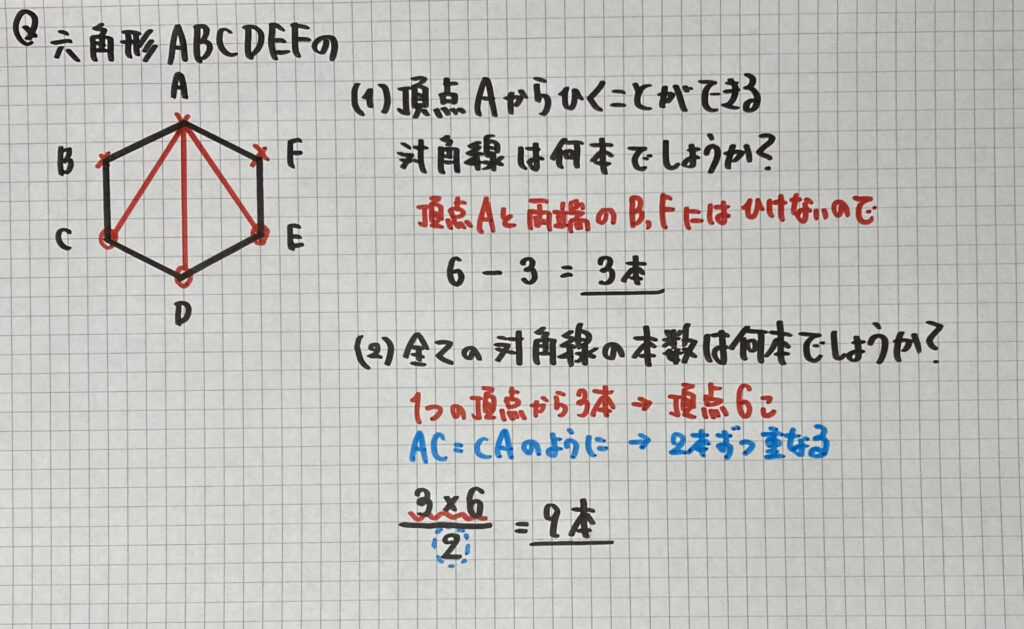
1つの頂点から
引くことができる対角線は
頂点の数から
- 「その頂点」
- 「隣の頂点」
- 「隣の頂点」
の「3本」を引いた本数になります
そこから
(2)の全ての本数を
求めることができます
対角線の公式

先ほどの問題より
で求めることが
できますね
あとは
この公式に当てはめて
2時方程式を解くと
求めることができました
二次方程式の利用②のまとめ

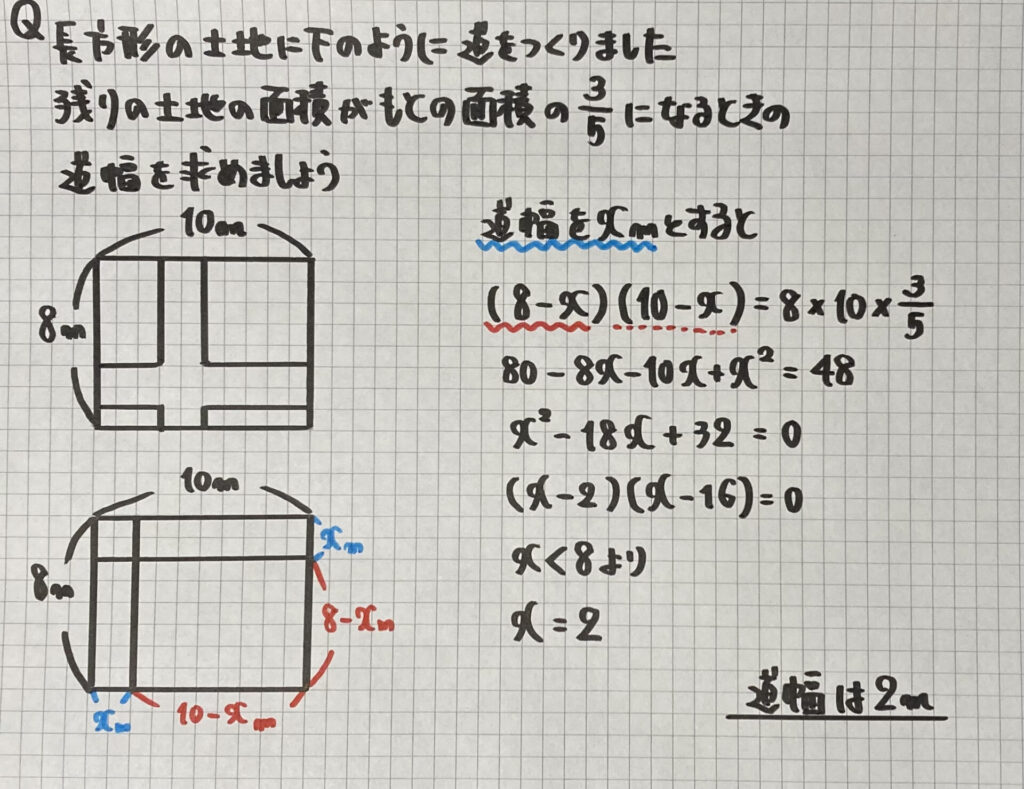
・「道幅」の問題
「道」を片側に寄せて考える
・長方形の周りの長さの式
(たて+よこ)×2=周りの長さ
- たて=$\frac{周りの長さ}{2}$−よこ
- よこ=$\frac{周りの長さ}{2}$−たて
・動点の問題
「動いた分の長さ」
を図形に書き込んで
・$n$角形の対角線の本数
$\frac{n(n−3)}{2}$(本)
かずのかず
以上、「数学嫌いな人が、
数学を楽しく好きになって欲しい」
かずのかずぶろぐでした