いよいよ
「中3数学」です
中1で「文字式の乗除法」
中2で「単項式の乗除法」
を学習してきました
こちらで
確認してくださいね
今回は
今まで学習した
「文字式の計算」の
考え方をもとに
「式の展開」を
一緒にやっていきましょう
多項式×単項式
「単項式」
と「多項式」は
大丈夫ですか

では
「多項式×単項式」
の計算を
やっていきましょう
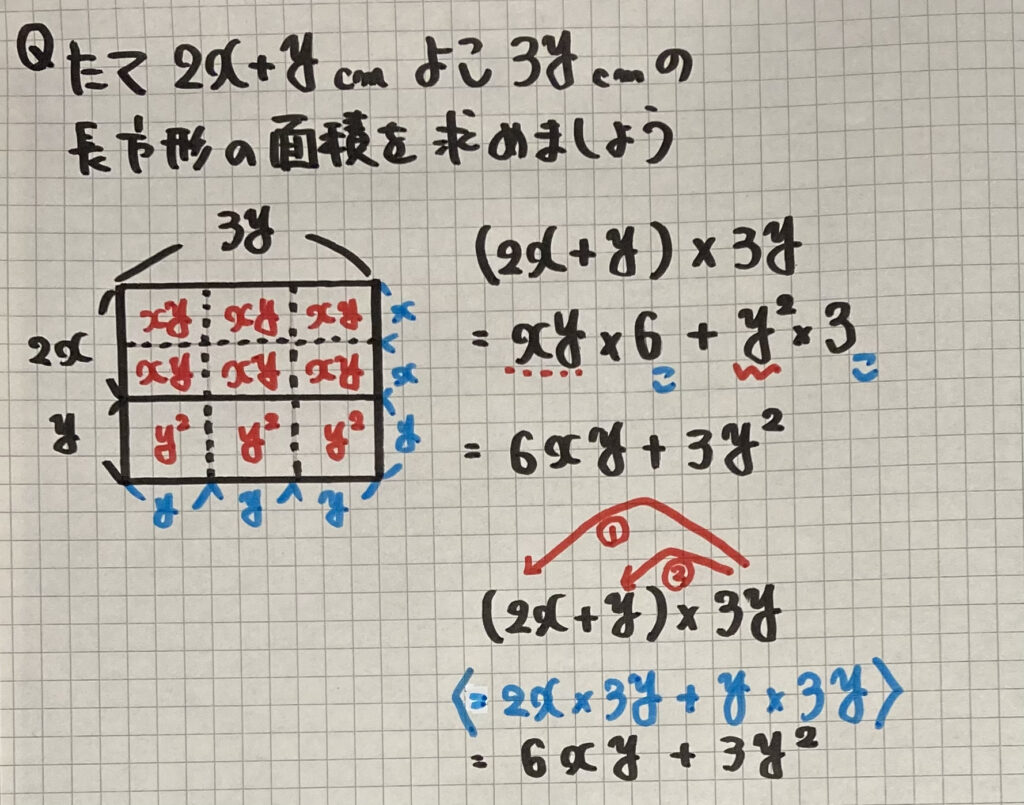
長方形の面積で
考えてみましょう
たて「$2x +y$」を
「$x$が2こ」「$y$が1こ」に分けて
よこ「$3y$」を
「$y$が3こ」に分けて考えると
↓
面積の合計は
「$xy$が6こ」「$y^2$が3こ」なので
「$6xy +3y^2$」
となりますね
ただ、毎回
「この分ける考え方」
をすると大変ですよね
「計算の意味」が
分かったので
次のように
やっていきましょう
$(2x+y)×3y$
=$2x×3y +y×3y$
=$6xy +3y^2$
練習問題
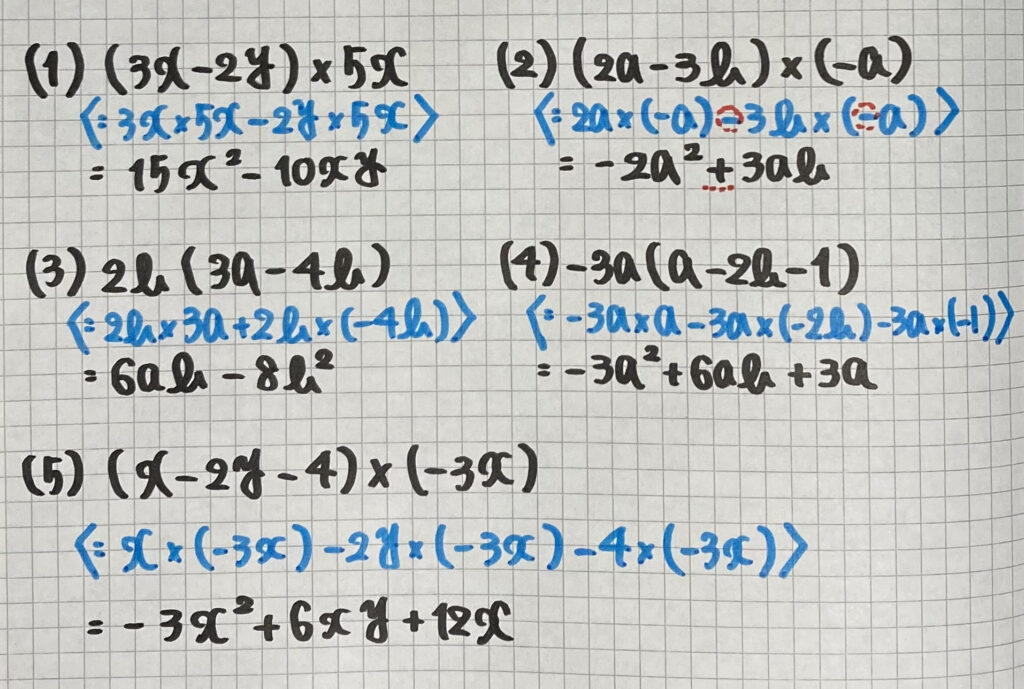
では練習問題です
慣れてきたら
2段目の<式>は
省略(頭の中で)
しても大丈夫です
多項式÷単項式

こちらも
長方形の面積
で考えてみましょう
ノートの
吹き出しにしましたが
面積の「$3x^2+2x$」を
「$x^2$が3こ」「$x$が2こ」に分けて
「面積÷たて=よこ」で
よこの長さ
「$x +x +x +1+1$」
=「$3x+2$」
を出すことができますね
ただ、今回も
「この分ける考え方」で
「計算の意味」が
分かったので
$(3x^2+2x)÷x$
=$3x^2÷x$+$2x÷x$
=$\frac{3x^2}{x}$+$\frac{2x}{x}$
=$3x +2$
このように
やっていきましょう
練習問題

では練習しましょう
(4)(5)のように
こちらも
慣れてきたら
2段目の<式>は
省略(頭の中で)
しても大丈夫です
多項式×多項式
こちらも
長方形の面積で
考えていきます
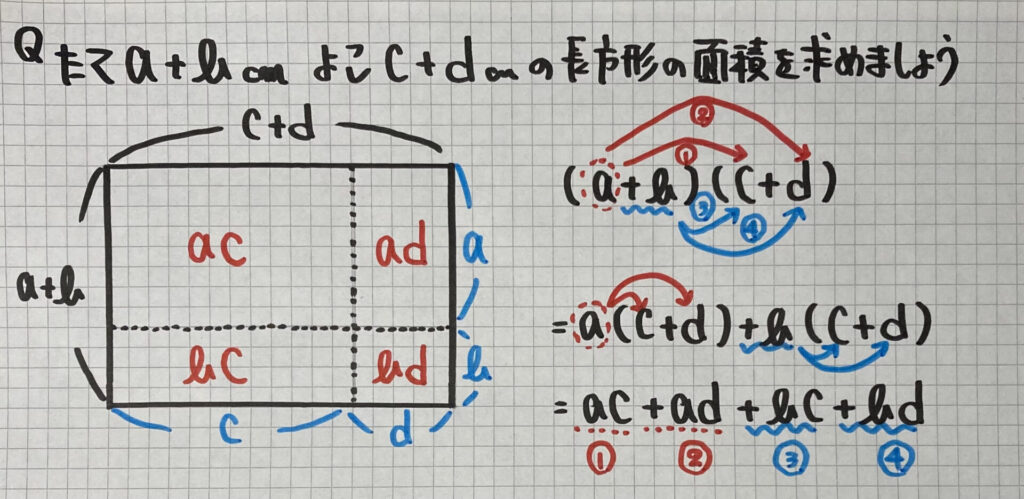
たて「$a +b$」を
「$a$」「$b$」に分けて
よこ「$c +d$」を
「$c$」「$d$」に分けて考えると
↓
面積は
「$ac$」「$ad$」「$bc$」「$bd$」
の4つの和
になりますね
練習問題

「分配法則を2回」使って
解くことができますね
慣れてきたら
2段目の<式>は
省略(頭の中で)
しても大丈夫です
(3)(4)(5)のように
式の展開(乗除法)のまとめ

・式の展開
$(a +b)(c +d)$<積の式>
↓(展開する)
$ac +ad +bc +bd$<和の式>
・多項式×単項式
$(a +b)×c$
<=$a×c +b×c$>
=$ac +bc$
・多項式÷単項式
$(a +b)÷c$
<=$a÷c +b÷c$>
=$\frac{a}{c}$+$\frac{b}{c}$
・多項式×多項式
$(a +b)×(c +d)$
<=$a(c +d) +b(c +d)$>
=$ac +ad +bc +bd$
慣れてきたら
2段目の<式>は
省略(頭の中で)
しても大丈夫です
以上、「数学嫌いな人が、
数学を楽しく好きになって欲しい」
かずのかずぶろぐでした