前回まで
いろいろな「三角形」
について学習してきました
今回からは
「四角形」について
学習していきます
まずは「平行四辺形」です
算数でも
「面積」
「対称な図形」
で学習しましたね
もう少し
図形について詳しく
一緒に見ていきましょう
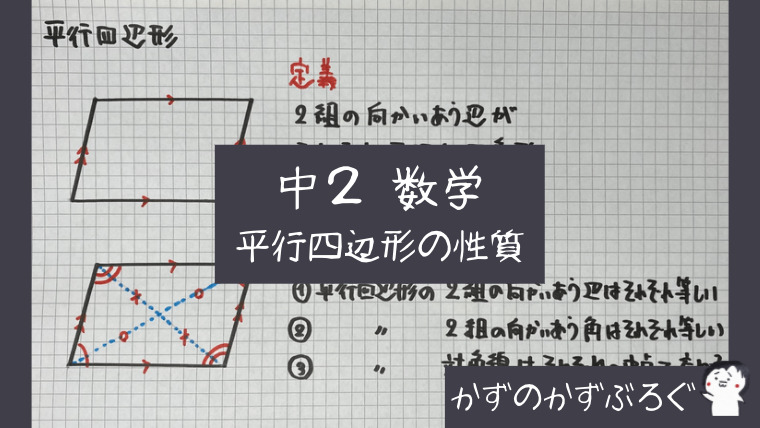
平行四辺形の定義と性質
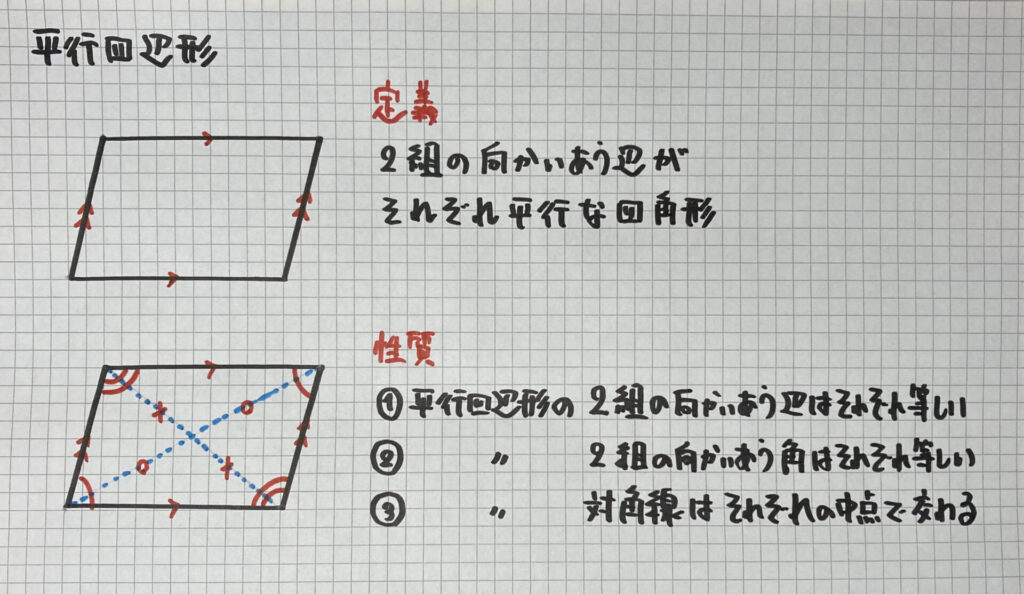
まずは
言葉の説明から
いきましょう
平行四辺形の性質②の証明
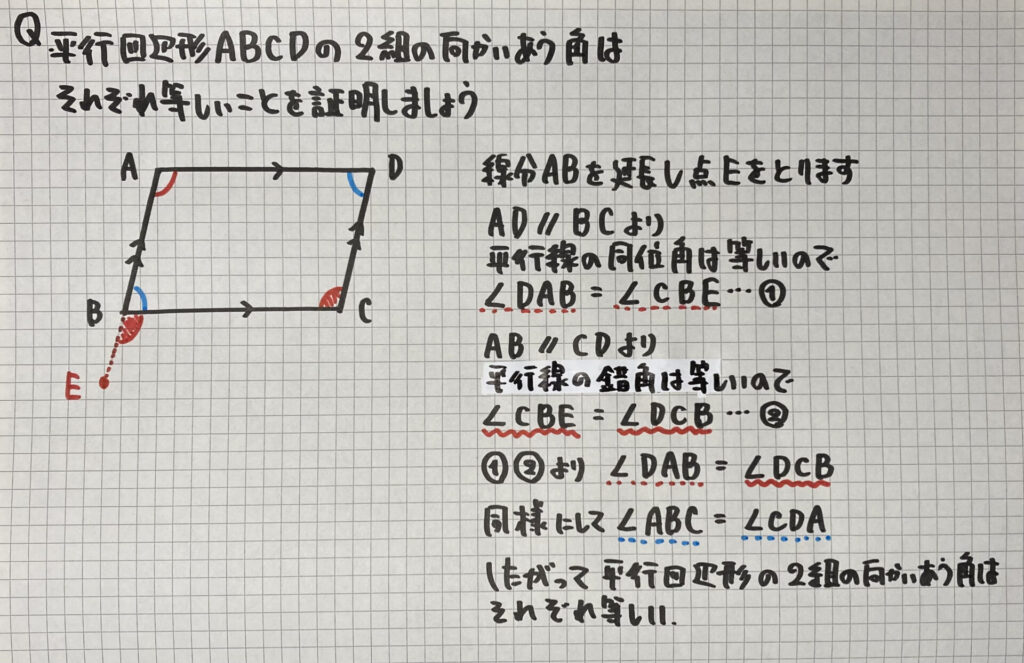
では
「平行四辺形の性質②」
- 2組の向かいあう角はそれぞれ等しい
の証明をやっていきましょう
平行な2直線の
- 同位角
- 錯角
は等しいことを利用しましょう
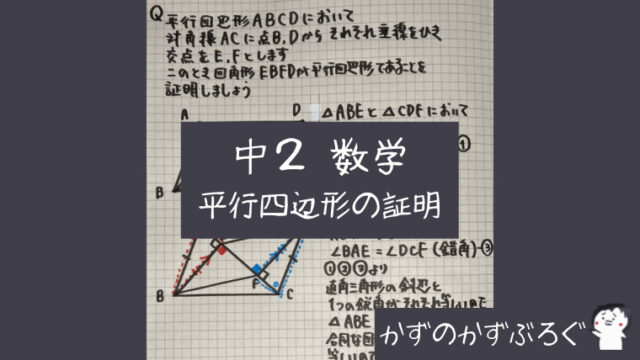
平行四辺形の性質③の証明

次に
- 対角線はそれぞれの中点で交わる
の証明をやっていきましょう
対角線AC BDの中点を証明する
↓
対角線の交点をOとする
↓
AO=CO BO=DOを証明する
↓
辺の長さが等しい証明
↓
合同な三角形の証明
この流れで考えます
まず「合同な三角形」
を探しましょう
問題に「平行四辺形」
とあるので
- AB=CD
- AB//CD
を利用しましょう
「平行線」が出てきたら
- 同位角
- 錯角
をチェックしましょう
この問題では
「錯角は等しい」で
合同を証明することが
できますね
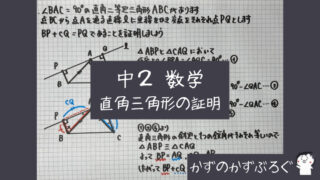
平行四辺形を利用した証明
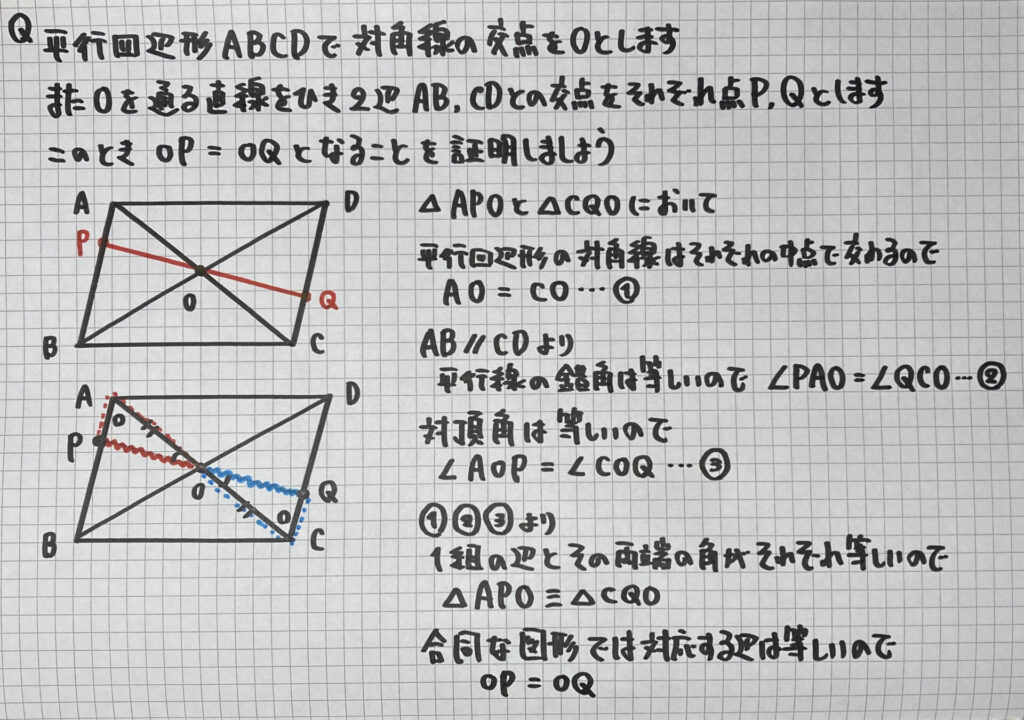
この問題は
OP=OQ
(辺の長さが等しい証明)
ということは…
そうですね
OP、OQが
対応する辺になっている
2つの三角形の「合同」を
証明しましょう
問題に「平行四辺形」
とあるので
- 対角線は中点で交わる
- AB//CD(錯角)
を利用しましょう
あと1つ等しいものは
「対頂角が等しい」を
利用しましょう
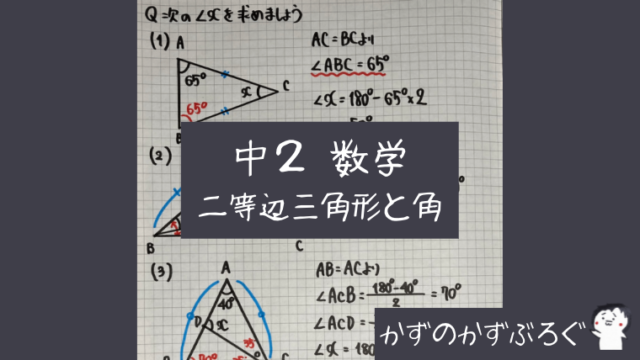
「平行四辺形の角」の問題

ノートの右側に
問題を「解く流れ」を
まとめました
この問題の
ポイントは2つです
平行四辺形
- 平行(錯角)
- 向かいあう角は等しい
二等辺三角形
- 底角が等しい
を利用して求めましょう
平行四辺形の性質のまとめ

・平行四辺形の定義
「2組の向かいあう辺がそれぞれ平行な四角形」
・平行四辺形の性質
平行四辺形の
- 2組の向かいあう辺はそれぞれ等しい
- 2組の向かいあう角はそれぞれ等しい
- 対角線はそれぞれの中点で交わる
・平行四辺形の角
平行四辺形
↓
2組の平行線(錯角・同位角)
↓
「二等辺三角形」
を作ることが多い
かずのかず
以上、「数学嫌いな人が、
数学を楽しく好きになって欲しい」
かずのかずぶろぐでした