前回は
「直角三角形の合同条件」
を学習しましたね
かずのかず
こちらで
確認してくださいね
【中2数学】「直角三角形の合同条件」の問題 どこよりも簡単な解き方・求め方前回までに、特別な三角形として「二等辺三角形」「正三角形」を学習しました 今回は「直角三角形の合同条件」について一緒に見ていきましょう...
今回は
「直角三角形の合同」
を利用して解く問題を
一緒に見ていきましょう
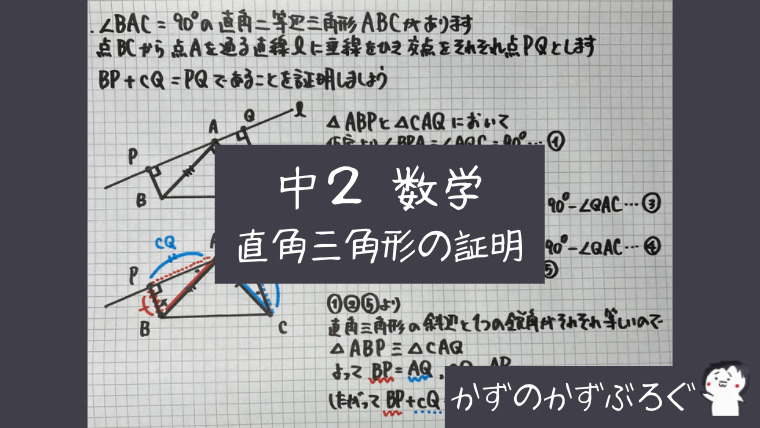
直角三角形の証明①
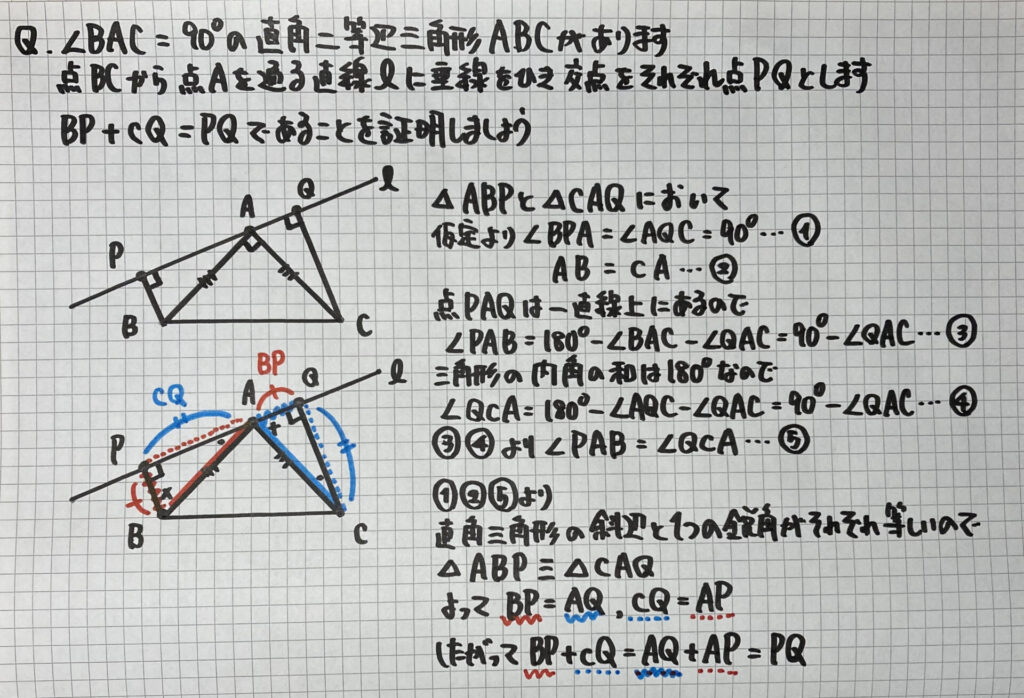
問題を見て
分かることは
3つの直角三角形がある
ということです
そして証明することが
辺の長さ(角の大きさ)が
等しいではなく
$BP +CQ=PQ$
等式が成り立つかを証明します
最初は
少し戸惑うかもしれませんね
ただ「合同」そうな図形があれば
合同を利用した証明
- 合同な図形を証明する
- 対応する辺(角)に注目する
- 対応する辺(角)で等式を立てる
- 結論を導く
の流れで
問題を解くことが
できます
今まであったかも
知れませんが
証明が全く書けない
(考えつかない)時は
書き写した後に
対応する辺(角)が
「どのように等式で使われている」
かを確認しましょう
(図形に印や色をつけることも大切です)
直角三角形の証明②
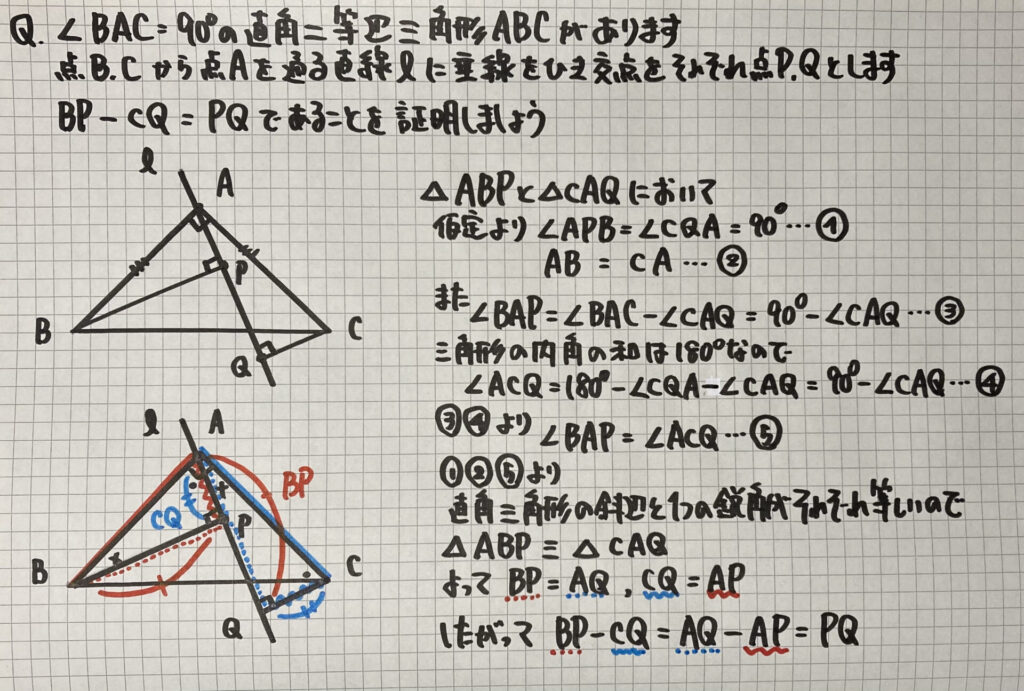
先ほどの①と
よく似た問題です
直線ℓが
△ABCの内部にある場合です
合同な三角形は
すぐに見つけることが
できると思いますが
等式
$BP -CQ=PQ$

「何をすれば…」
と最初はなるかも
知れません
証明の問題には
「慣れていくしかない」
ので何度も書いて
練習しましょう
そうすれば
「書けるようになります」
また
繰り返しになりますが
直角三角形の証明③
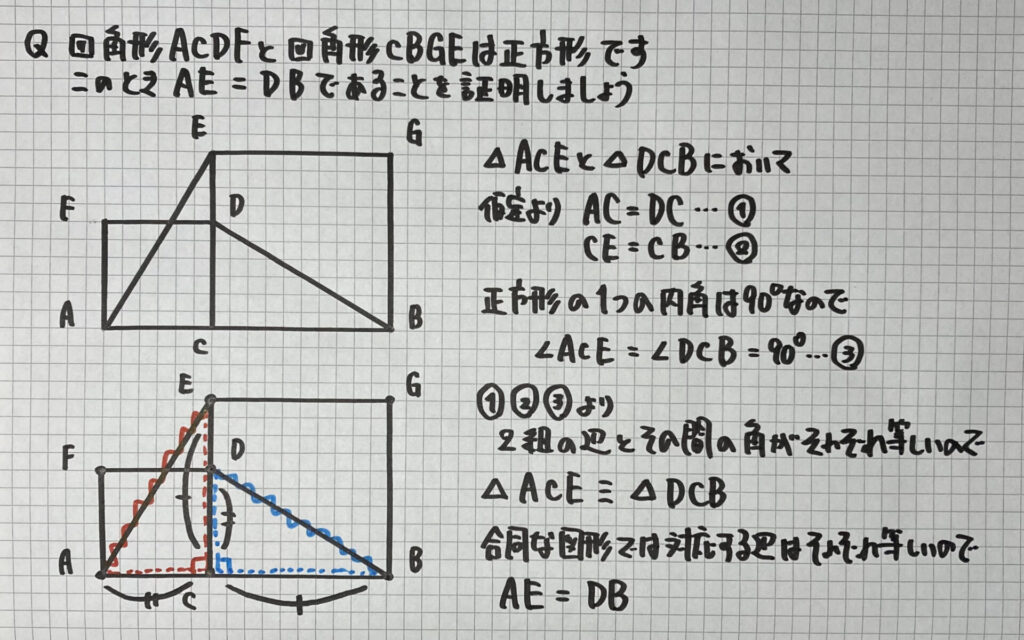
最後に
直角三角形の合同条件が使えない
「直角三角形の合同」を証明する問題です
こんな時は
以前学習した
を使って証明しましょう
直角三角形の証明のまとめ

・合同を利用した証明
- 合同な図形を証明する
- 対応する辺(角)に注目する
- 対応する辺(角)で等式を立てる
- 結論を導く
・直角三角形の合同条件が使えない時
斜辺が「結論」になっている等…で
2つの
「直角三角形の合同条件」
が使えない時は
以前学習した
三角形の合同条件
- 3組の辺が、それぞれ等しい
- 2組の辺とその間の角が、それぞれ等しい
- 1組の辺とその両端の角が、それぞれ等しい
を使って証明しましょう
かずのかず
以上、「数学嫌いな人が、
数学を楽しく好きになって欲しい」
かずのかずぶろぐでした