【小5算数】「正多角形と円周の長さ」の問題　どこよりも簡単な解き方・求め方

今回は図形の内容です

キレイな形の「正多角形」「円」についてです

図形の特ちょうや性質を見ていきましょう

正多角形とは

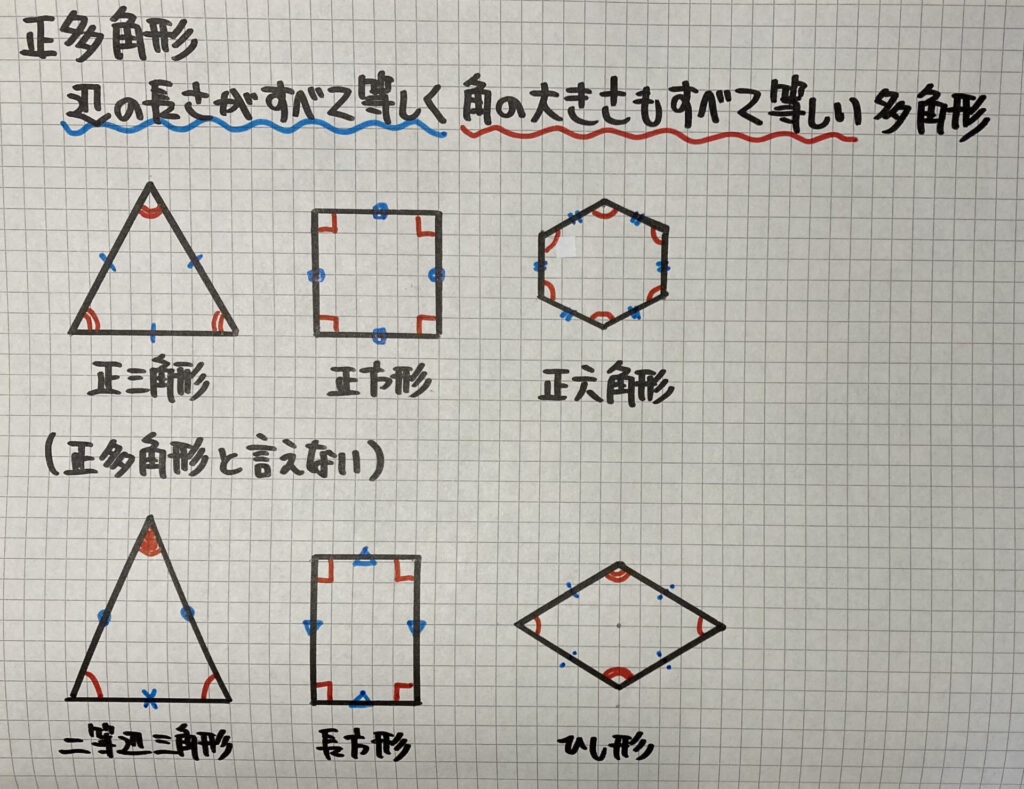
下の3つは「正多角形」とは言えません

「二等辺三角形」は3辺のうち「2辺」だけ等しく、

3つの角のうち「2角」だけが等しいです

「長方形」は「角」はすべて等しいのですが

辺の長さは「向かい合う辺」のみが等しいです

「ひし形」は「辺」はすべて等しいのですが

角の大きさは「向かい合う角（対角）」のみが等しいです

練習問題

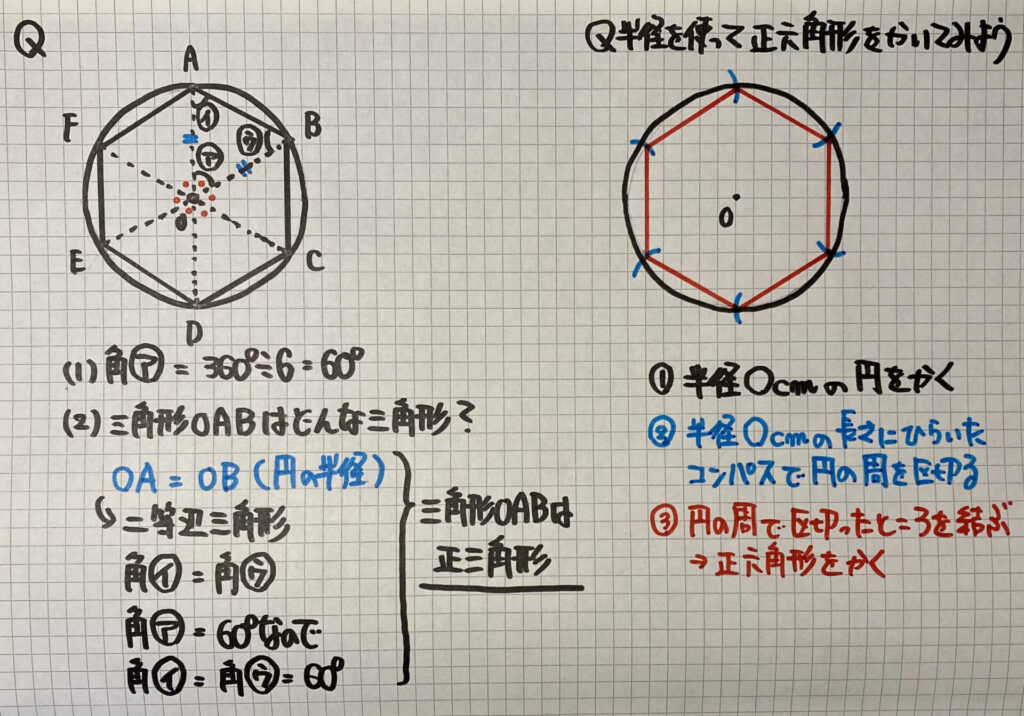
円の中にある「正六角形」は

「正三角形」「6つ」でできています

⑴の角アは

「1回転360°」を「6等分」しているので

360°÷6＝60° となります

⑵は、まず「円の半径は等しい」より

OA＝0Bなので「二等辺三角形」と言えます

さらに角度を見てみると

二等辺三角形より、

「角イ=角ウ」で「角ア」は「60°」なので

すべての角が「60°」となり

三角形OABは「正三角形」です

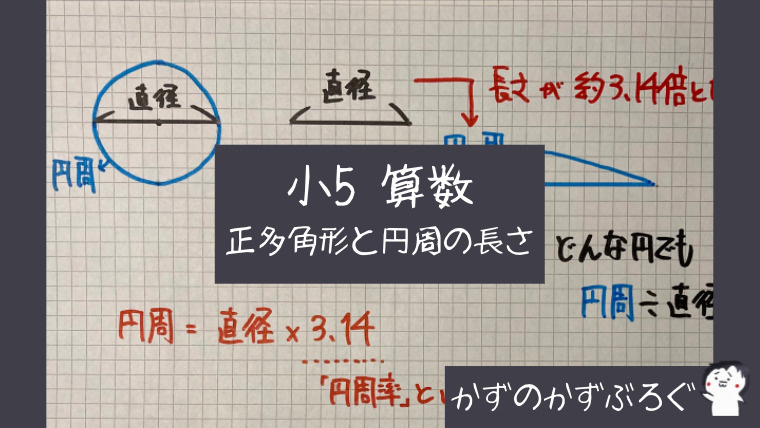
円周（円の周りの長さ）

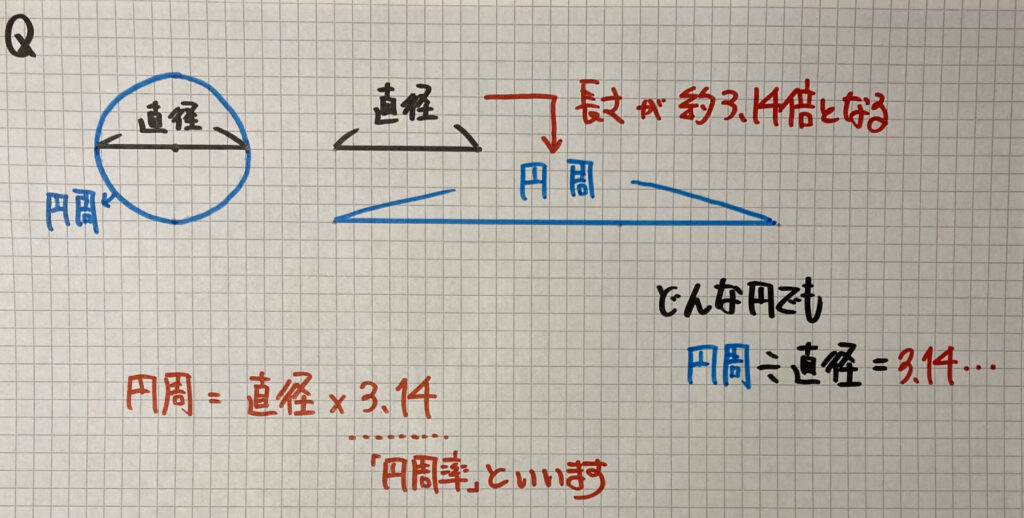
どの円も、「円周の長さ」は「直径」に「ある数」をかけたものになります

この「ある数」のことを「円周率」と言います

円周率＝円周÷直径で求めることができますが

「3.14159265359…」と「わり切れない数」なります

小学校では「3.14」を使って計算していきます

練習問題

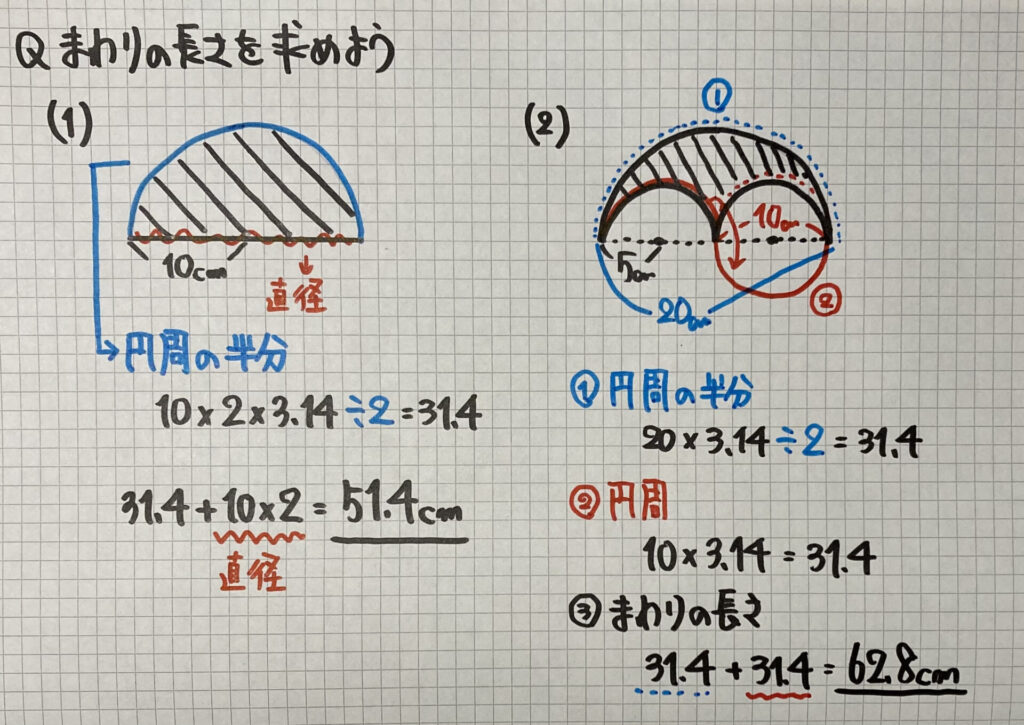
⑴は「周りの長さ」を求める問題です

「円周」を、求める問題ではないので

「直径」を足すのを最後忘れないように注意しましょう

⑵は左の小さな「半円」を右の「半円」と合わせます

すると、「大きな円の半円」と「小さな円の円周」で

求めることができます

正多角形と円周の長さのまとめ