【小5算数】「分数のたし算ひき算」の問題　どこよりも簡単な解き方・求め方

ここでは「分数のたし算ひき算」をやっていきます

大事なことは2つ

• 通分（分母を等しくする）
• 約分（分数の大きさを変えず、分母分子を小さくする）

また、「分数」を使った「時間」の

考え方についても見ていきましょう

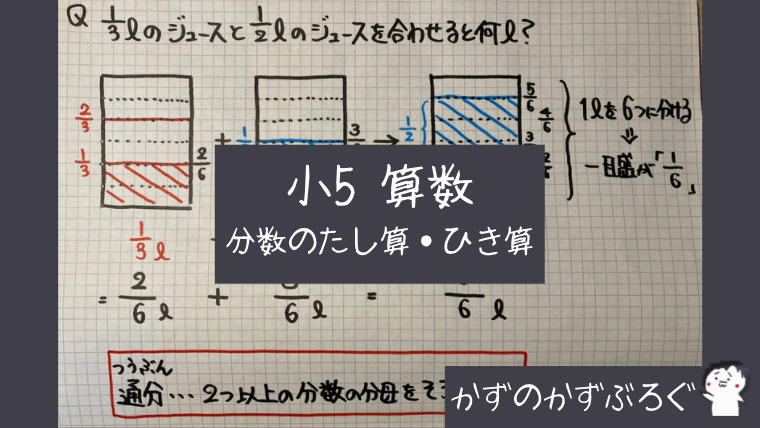
通分（分母がちがう分数の計算）

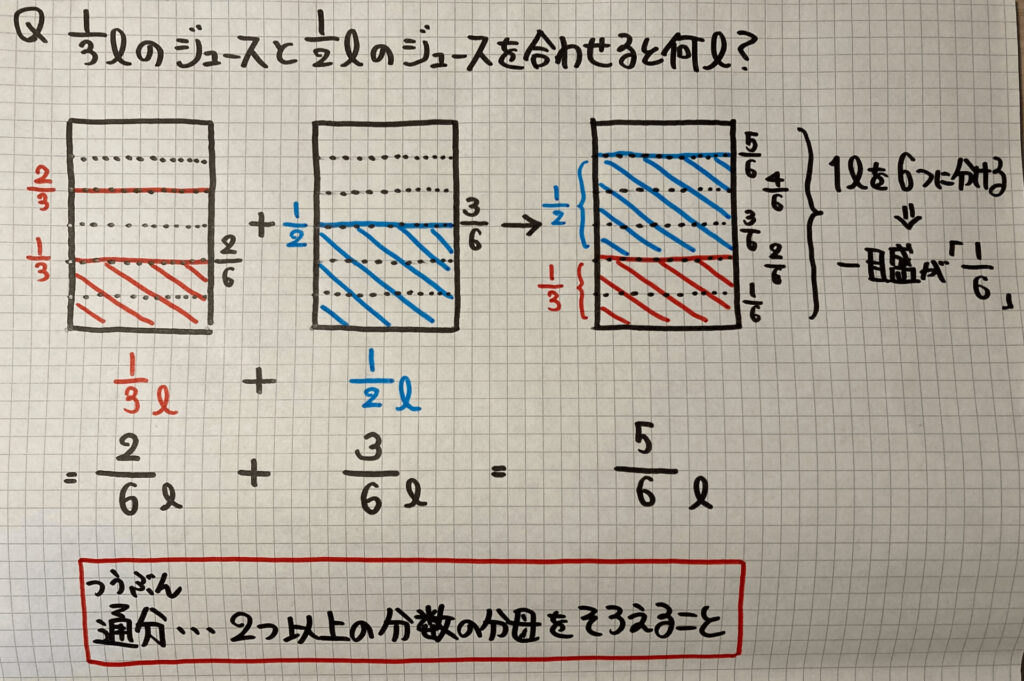
分母がちがう分数のたし算を考えるとき

分母をそろえて（通分して）計算しないといけません

ここでは、分数の分母を

「目もり」の大きさで表しています

大きさの等しい分数

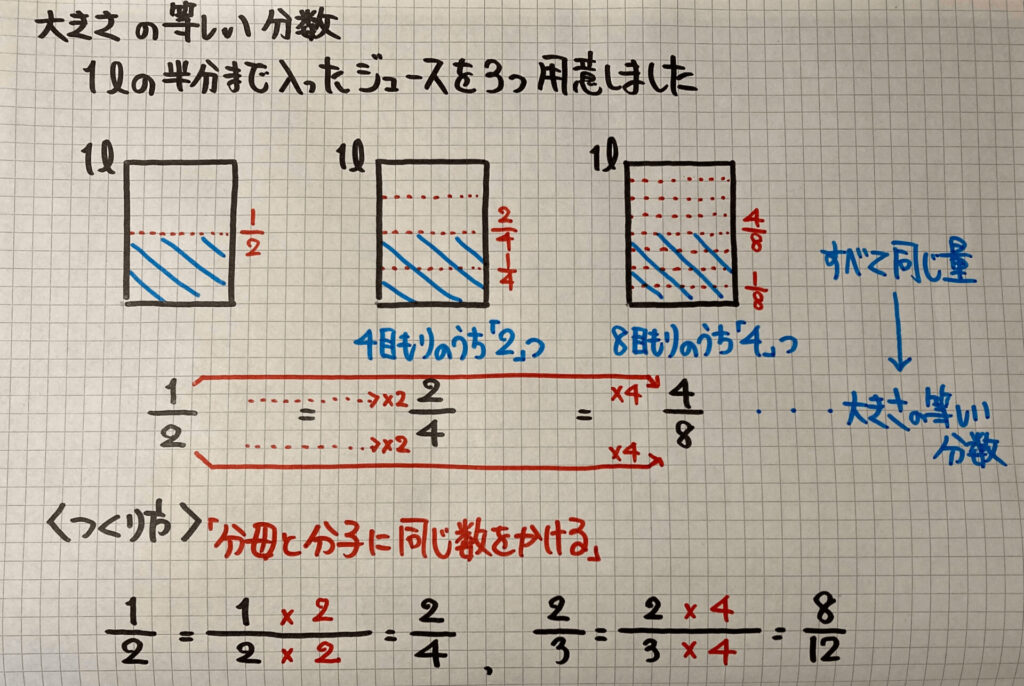
分数は

「分母」と「分子」に同じ数をかけることによって

大きさの等しい分数を作ることができます

約分（分母分子を小さくする）

先ほどの「大きさの等しい分数」の考え方を使って

今度は「分母」と「分子」を同じ数でわることによって

小さくすることができます

これを約分と言います

計算練習

これから大切なルールが1つ増えます

⑶では「3つの分数」の計算を行いました

「3つの分数」の「通分」は「最小公倍数」で

求めることができます

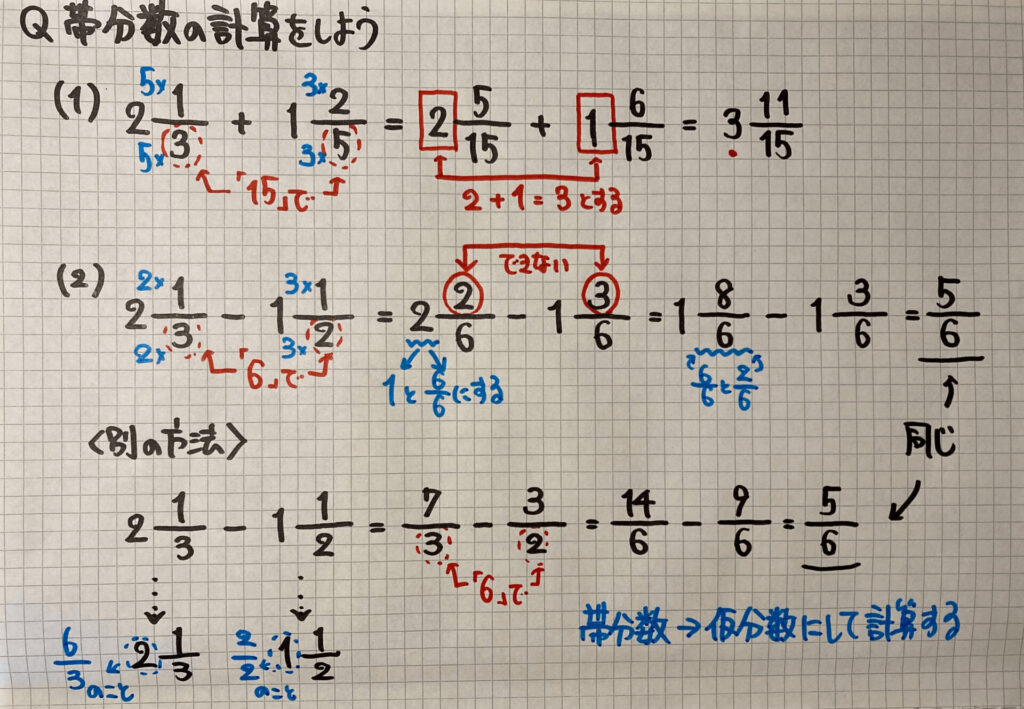
帯分数の計算は

たし算…「整数部分」をそのまま計算しましょう

ひき算…「分数部分」が計算できないとき

　　　　「仮分数」に直して計算をしましょう

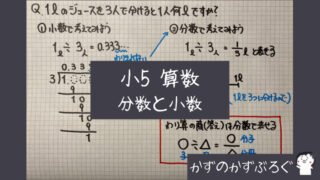
分数と小数の計算

⑴は「分数」を「小数」にすることができるので

「小数」で答えを出しています

⑵は「分数」を「小数」にすることができないので

「分数」で計算をしています（約分を忘れないようにね！）

⑶は「小数」を「分数」にするときに

「約分」をしてから計算しています

時間と分数

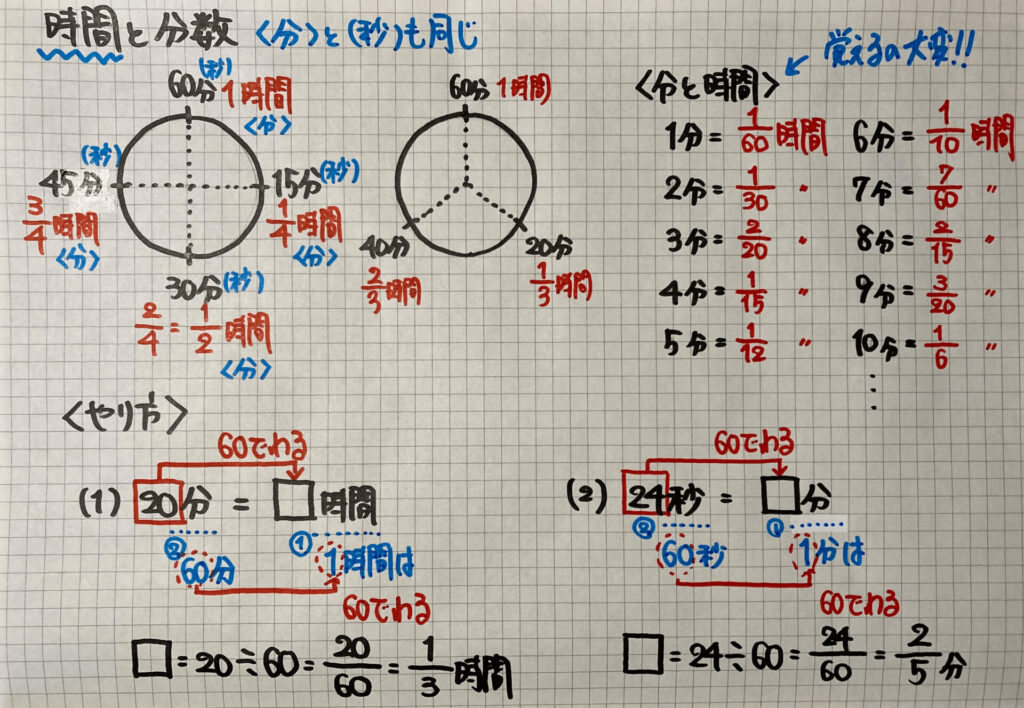
「分数」を使うと

「15分」や「30分」等

すべての「分」を「時間」で表すことができます

右側に「約分」をした「1分」から「10分」を

書きましたが、覚える必要はありません

＜やり方＞を見ながらできるようになってください

①単位の下をそろえます　

「1時間＝60分」と書きましょう

②求めたい□の

単位の「数」を見ます

「60」分　⇨　「1」時間

③「60」を＜60でわる＞と「1」になるので

「20」を＜60でわる＞と□を求めることができます

文章で書くとむずかしくなるので

上のノートで確認してくださいね

覚えていないといけないことは

これだけです↓

分数のたし算ひき算のまとめ