【小5算数】「割合」の問題　どこよりも簡単な解き方・求め方

「Aさん、バスケットのシュート上手だな」

「Bさんも上手いけど、どっちの方が上手なんだろう」

算数では、こんな時

「どちらの人がよくシュートを成功するか」を

計算で求めることができます

この時に使う考え方を「割合」と言います

「割合」には、下の2種類の数（量）が出てきます

• もとにする量
• 比べられる量

そして「割合」の意味は

「ある量（数）をもとにして、

　比べられる量（数）が

　もとにする量の何倍にあたるかを表したもの」です

この言葉を覚える必要はありません

言葉にすると難しく感じるので

実際に問題で見ていきましょう

もとにする量と比べられる量

この問題の

比べられる量…シュートが入った数

もとにする量…シュートの本数　です

という公式はありますが、

これも覚える必要はありません

「割合」の問題で

「かけ算」か「わり算」どちらの式を使うかで

迷ったり、間違えてしまうことがありますが

ノートのように

割合の問題は

文章から「かけ算」の式を作ることが大切です

百分率と歩合

「果汁100%のジュース」

「野球の打率　2割7分4厘」などを

聞いたことはありませんか

これらは「割合」を表すもので

• 「％」…百分率（ひゃくぶんりつ）
• 「割（わり）分（ぶ）厘（りん）」…歩合（ぶあい）

と言います

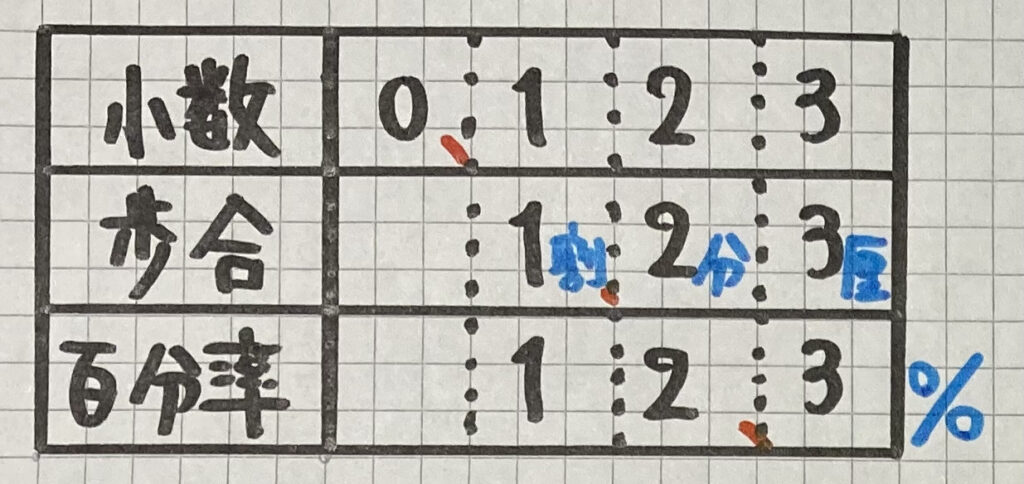
まず、左の表で

「小数（整数）」と「歩合」と「百分率」の

関係をまとめました

最初は、問題をやるときに

この表を見ながら練習してみましょう

練習問題

文章題を解く時の大切なことは3つです

• 「は」を「＝（イコール）」にする
• 「何」を「□」にする
• 「割合（百分率・歩合）」を「小数」にして「倍」をつける

そこから「かけ算の式」を作ることです

⑷は、最初の文章では、

少し「かけ算」の式を作りにくいので

文章の形を変えています

□を求める時に

「かけ算」か「わり算」の

どちらを使うかを考えましょう

原価　定価　売価　利益とは

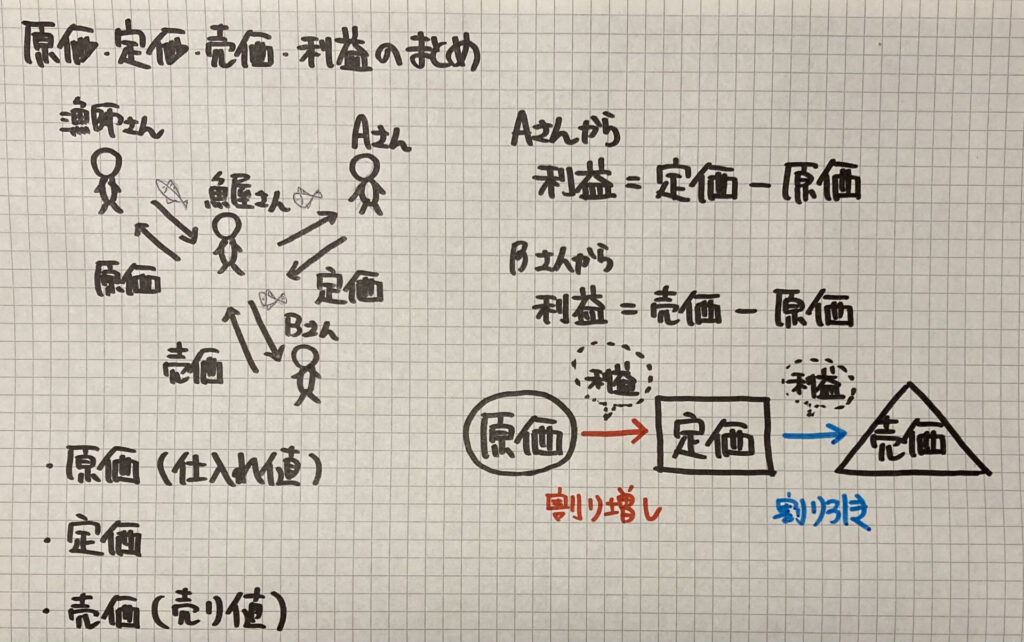
左の図は

魚屋さん、漁師さん、魚を買いにきたAさん、Bさん

の「魚とお金の流れ」を表したものです

まず、言葉の意味です

・「原価（仕入れ値とも言います）」

　　⇨物を仕入れる時の値段です

・「定価」

　　⇨原価に利益をつけて売るときの値段です

・「売価（売り値）」

　　⇨定価で売れないとき等に、

　　　値段を安くして売る時の値段です

・「利益」には、2種類あり

　「定価で売った時」と「売価で売った時」があります

・「割り増し」

　　⇨「原価」に「利益」をつける時の考え方

・「割り引き」

　　⇨「定価」を「売価」にする時の考え方

分かりにくかった人は

もう一度、ノートを見てイメージをつかんでくださいね

割り引き

「割り引き」は、買い物の時に

見たことがあるかもしれませんね

「割り引き」の問題の

やり方は2種類あります

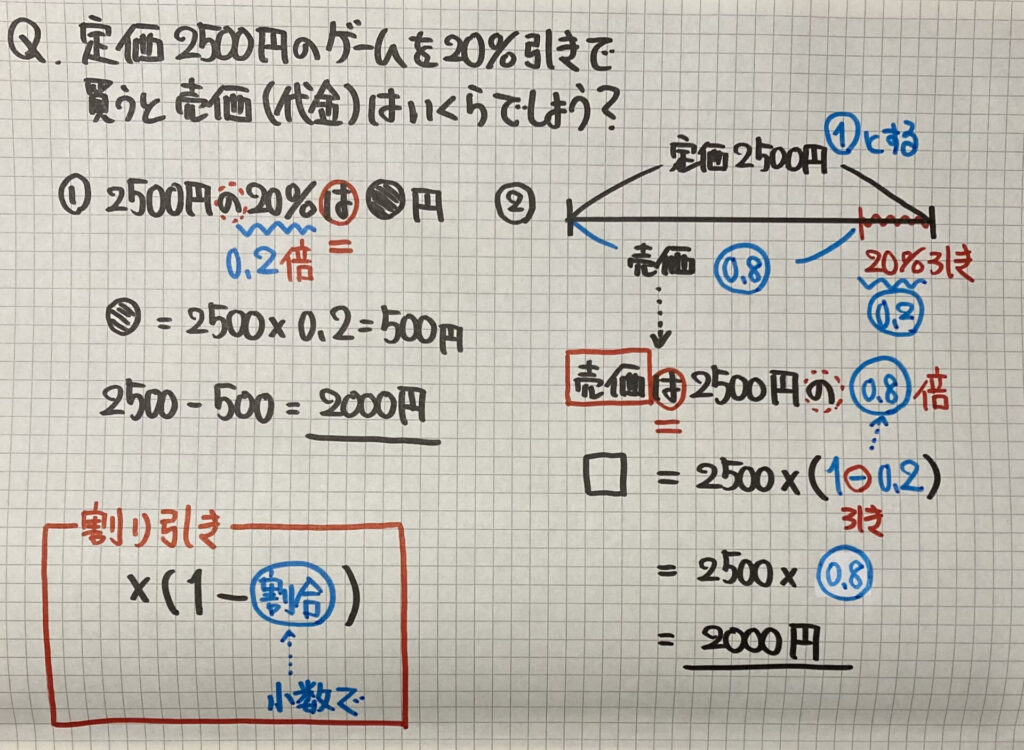
①「割り引き」された「値引き額」を計算します

　「売価」＝「定価」-「値引き額」

②「売価」の「割合」を求めます

　　20％引きを「割合」で考えると

　「1」-「0.2」＝「0.8」となります

　「売価」＝「定価」×（1-0.2）

どちらの求め方でも答えを出すことができますが

②で求める方が

割り増し

「割り増し」は、商売をするとき

（定価を決める）の考え方です

「割り増し」の問題の

やり方は2種類あります

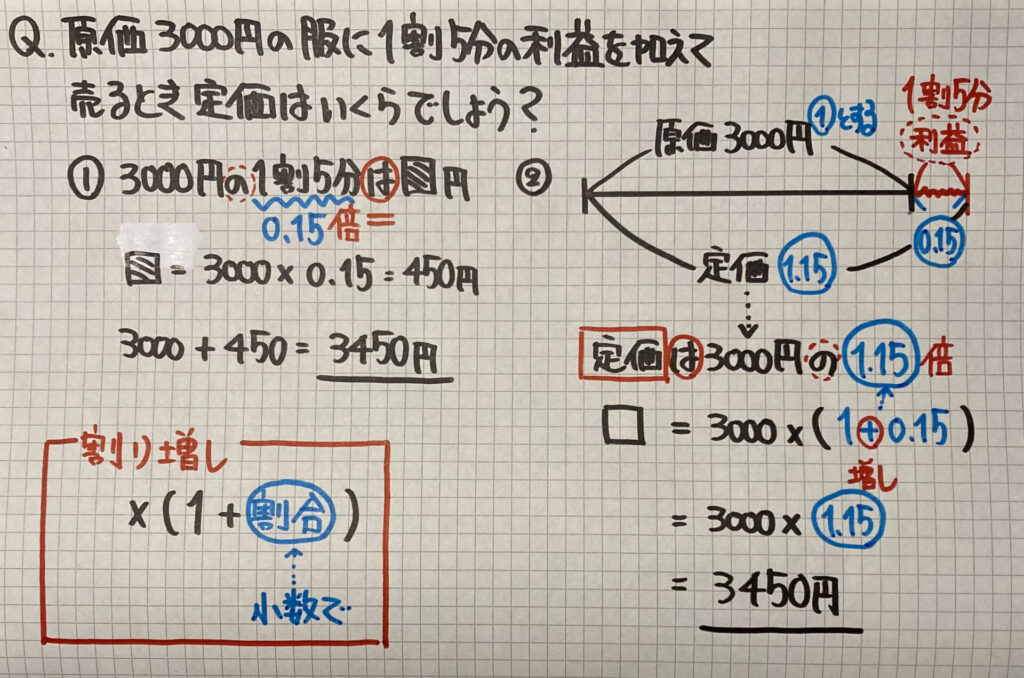
①「割り増し」された「利益」を計算します

　「定価」＝「原価」+「利益」

②「定価」の「割合」を求めます

　　1割5分を「割合」で考えると

　「1」+「0.15」＝「1.15」となります

　「定価」＝「原価」×（1+0.15）

どちらの求め方でも答えを出すことができますが

「割り増し」も

②で求める方が

割合のまとめ