前回、「倍数」の勉強をしました
今回は「約数(やくすう)」です
名前はよく似ていますが
考え方は、「倍数」とは反対のイメージです
今回は「倍数」のときに出てきた言葉に
よく似た言葉が出てきます
間違えないようにしっかりおさえていきましょう
では、くわしくいっしょに見ていきましょう!
約数と公約数とは
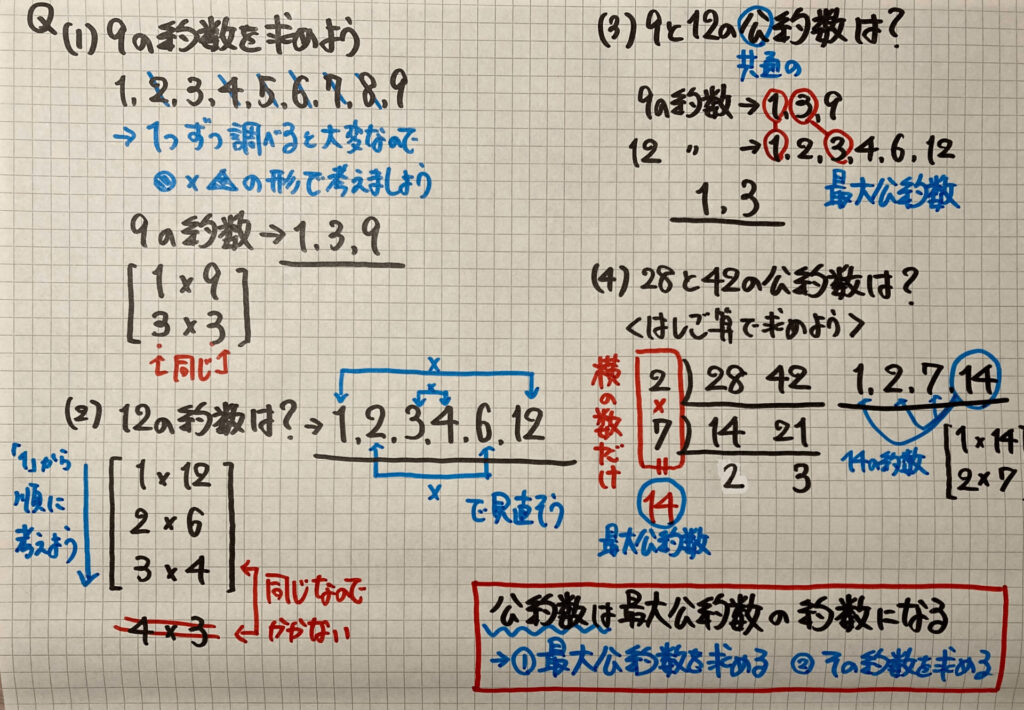
まずは言葉の説明から
ここで、もう1つ
⑶のように公約数を求めるときは
「それぞれの約数を順番に書いていき
共通しているものを探していく」というのが1つのやり方ですが
最大公約数を見つけて
その数の約数を調べると
公約数を見つけることができます
それを言葉にすると
となりますが、覚える必要はありませんので心配いりません
意味だけ分かるようにしておきましょう
それと「最大公約数の求め方(はしご算)」
を⑷で説明しています
「わり算のひっ算」を逆さまにしたような形です
一度わかると、とても役に立ちます
文章題(正方形をしきつめる)

次は、とても有名な文章題です
色々な教科書、問題集で出てきて
まちがえる人が多い問題です
「最小公倍数の文章題(正方形を作る)」
とよく似ているので気をつけましょう!
例えば、「長方形の紙」の中に
いろんな大きさの「正方形の紙」をしきつめていくと
- きっちり、しきつめることができるときと
- すきま(正方形の紙が置けない場所)があるときがありますね
では、どんな大きさの「正方形の紙」を並べていくと
すきま無く、きっちりしきつめることができるでしょうか
ちょっと長かったですが
文章にするとこんな問題です

文章ばかりで長くなったので ちょっと、休憩…
さあ、いきましょう!
図を書いて求めていくこともできますが
問題によってはとても大きくなってしまうことが
あるので
表などに「たて」と「横」の長さを
まとめて考える方が良いですね
「たて12cm」「横20cm」で
「たてと横の長さが同じになる」ということは
「12」と「20」の約数で
「同じものを探せば良い」ということですよね
そして、正方形が「最大」ということは
つまり
ということです
ここからは、かんたんですね!
3つの数の公約数

最後に「3つの数」の
「最大公約数」を求める問題です
上のように、順番に書き出していくこと
で求めることができますね
また、ここでも「はしご算」を使って
求めることもできます
約数 公約数のまとめ

・約数とは「ある整数をわり切ることができる数」のこと
・約数の求め方は、かけ算の形(●×△)を作る
・公約数とは「2つ以上の整数に共通な約数」のこと
・公約数は「最大公約数の約数」である
・はしご算で
「3つの数の最大公約数」を求めるとき
- すべての数でわることができるときだけ、わり算を進める
- 外の「左側の数だけ」をかける
この2つにくれぐれも注意してくださいね!
以上、「算数嫌いな人が、
算数を楽しく好きになって欲しい」
かずのかずぶろぐでした