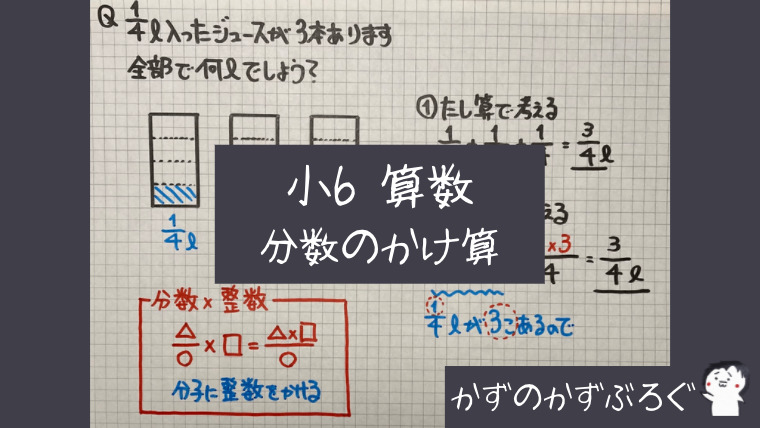
全部で何ℓになるでしょう
「3こ」ぐらいの量なら
「たし算」でも大丈夫ですが
これが、「10こ」「20こ」…となると
「たし算」でやるのは大変ですが
ここで役に立つのが「かけ算」ですね
「整数」のように
もちろん「分数」でも使えますが
いくつか気をつけることがあるので
一緒に見ていきましょう
分数 × 整数

まずは、分数×整数です
$\frac{1}{4}$ℓが入っている容器に注目してください「3つ」に同じ「目もり」が入っています
ここでの「目もり」は「分母」の「4」を表しています
この$\frac{1}{4}$が「3つ」あるとき「分母」の「4」は変わらず
「分子」の「1」が「3つ」あると考えることが
できますね

言葉で説明すると、「うーん…ややこしい」と
なるかもしれないので
上のノートでよく確認してくださいね
練習問題

では、実際に「分数×整数」を練習してみましょう
ここでの注意は、答えが
- 「仮分数」⇨「帯分数」に
- 「約分を必ずすること」です
⑶’を見てください
「計算の最後」に「約分」をしても良いですが
計算が楽になることが多いので
分数 ÷ 整数
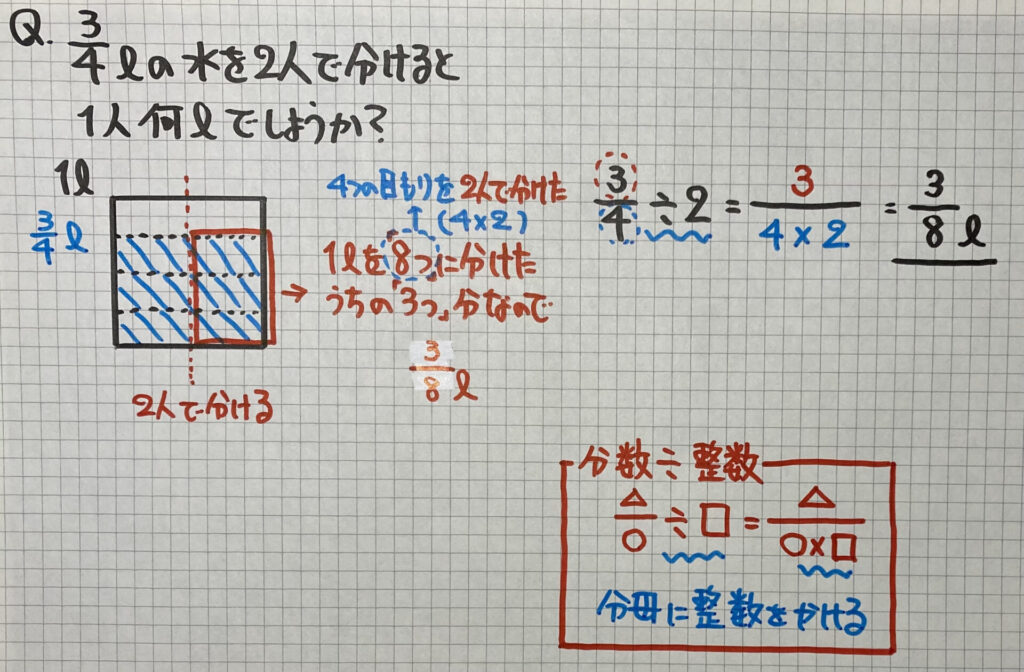
次は、分数÷整数です
$\frac{3}{4}$ℓが入っている容器に注目してください最初の「目もり」は「4」で「分母」を表しています
これを「2人」で分けるので
「目もり」は「2倍」になって
「4」⇨「8」になりますね
その時、「1人分」の「水」は
1ℓを「8つ」に分けたうちの「3つ」なので
$\frac{3}{8}$ℓとなります「分子」の「3」は変わらず
「2人」で分けたので「目もり」が「2倍」になる
「分母」の「4」が「8」になると
考えることができますね

またもや…
言葉で説明すると、「うーん…ややこしい」と
なるかもしれないので
上のノートでよく確認してくださいね
練習問題

では、「分数÷整数」を練習してみましょう
ここでの注意も、答えが
- 「仮分数」⇨「帯分数」に
- 「約分を必ずすること」です
⑶’は「約分」をしてから計算(分母×整数)をしました
分数 × 分数

さあ、分数×分数です
「たてが$\frac{2}{3}$m」 「よこが$\frac{1}{4}$m」の 長方形が「1辺 1mの正方形」の中にあると見てください
たての「目もり」は「3」で
よこの「目もり」は「4」です
正方形を「3×4=12こ」に分けています
この長方形の面積は
「1㎡の正方形」を
「12こ」に分けたうちの「2こ分」なので
$\frac{2}{12}$=$\frac{1}{6}$㎡と考えることができますね式を見てみると
練習問題

では、「分数×分数」を練習してみましょう
ここでの注意も、答えが
- 「仮分数」⇨「帯分数」に
- 「約分を必ずすること」です
⑶’は「約分」をしてから計算(分数×分数)をしました
計算のくふう

整数でできる「計算のくふう」ですが
もちろん「分数」でも使うことができます
問題に「必ず使って…」となかったら
無理して「計算のくふう」を
使う必要はありませんので
がんばって計算をして
答えを出しても、もちろん大丈夫です!
逆数(ぎゃくすう)

⑷⑸のように「小数」が出てきたら
まず「分数」にしてから「逆数」にしましょう
分数のかけ算のまとめ

・$\frac{分子}{分母}$×整数=$\frac{分子×整数}{分母}$
・$\frac{分子}{分母}$÷整数=$\frac{分子}{分母×整数}$
・$\frac{分子}{分母}$×$\frac{分子}{分母}$=$\frac{分子×分子}{分母×分毋}$
・計算するときの注意
「約分」してから「かけ算」をする
答えの「仮分数」は「帯分数」にする
・逆数
ある数に対して、かけると「1」になる数
<作り方> 分母と分子を入れかえる
以上、「算数嫌いな人が、
算数を楽しく好きになって欲しい」
かずのかずぶろぐでした