【小6算数】「分数のわり算」の問題　どこよりも簡単な解き方・求め方

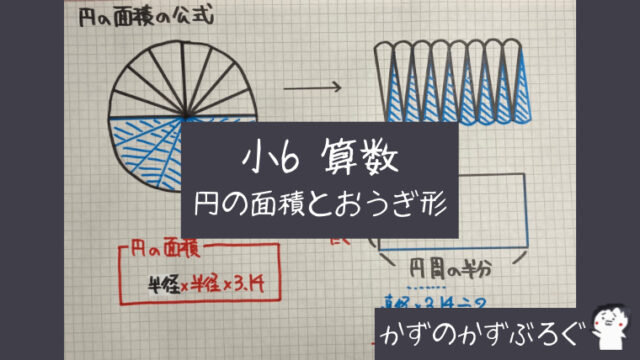
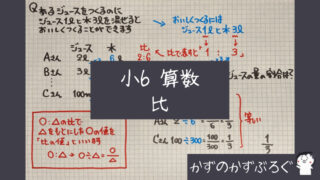
今回は「分数÷分数」を見ていきます

今まで勉強してきた

分数についての

「通分」「約分」そして

「かけ算」についての考え方を使って

やっていきましょう

【小5算数】「分数のたし算ひき算」の問題　どこよりも簡単な解き方・求め方通分とは2つ以上の分数の分母をそろえること（最小公倍数で考えよう）　約分とは分母と分子を同じ数でわって簡単に（数を小さく）すること　分数の計算の答えは「約分」しなければならない　「分数」を「小数」にできないときは式のすべての数を「分数」にして計算しましょう　「時間と分数」は「単位」に注目しよう...

【小6算数】「分数のかけ算」の問題　どこよりも簡単な解き方・求め方「整数」のように、もちろん「分数」でも「かけ算」は使えますが、いくつか気をつけることがあります。「分母どうし」「分子どうし」をかけること　「約分」をしてから「計算」をする　答えの「仮分数」は「帯分数」にする　また、「逆数」は、ある数に対してかけると「1」になる数のことです...

こちらで確認してみてくださいね

分数÷分数

左で復習しているように

分数は

　＜通分＞分母と分子に同じ数を「かけて」も

　＜約分＞分母と分子に同じ数で「わって」も

大きさは変わりませんね

この考え方を使って

右側の式を順番に見ていきましょう

式の中にある

「÷」を全て消して「×」の式にすることが

できました

練習問題

⑴⑵の

大きな分数で書いている（青い（）の）部分は

慣れてきたら、省略しても大丈夫です

⑷の÷整数を「逆数」にするとき

$\frac{整数}{1}$→$\frac{1}{整数}$　のようにしましょう

⑸の「×」「÷」が混ざっている式は

「×」だけの式にしてから計算します

⑹のように「小数」が混じっている式は

まず「小数」を「分数」にしてから計算をしましょう

文章題

【小5算数】「単位量あたりの大きさ　速さ」の問題　どこよりも簡単な解き方・求め方文章で出てくる「〜あたり」は「〜」の「単位」でわることで求める　人口密度＝人数÷面積（㎢）　速さとは、1時間（分・秒）あたりに進む道のり　速さの文章題は必ず、単位をそろえてから計算する...

こちらで確認してみてくださいね

⑵では

「分からないもの」を「$x$」にして

文章から、式を作って求めています

分数のわり算のまとめ