今回は「比例」です
「算数」でも学習したのは
覚えてますか?
「数学」なので
「負の数」が出てくるので
気をつけていきましょうね
算数の比例は
こちらで確認してくださいね

関数とは(変数と変域)
比例の前に
まずは「関数」「変数」「変域」に
ついて見ていきましょう

ノートにも書いていますが
まとめておきますね
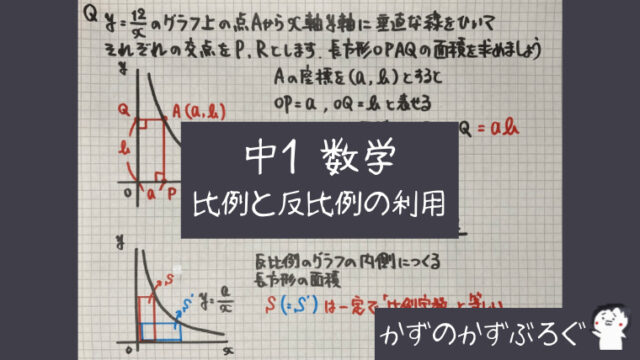
比例の式

⑴本が「1」冊の時、代金は「400」円ですね
→$x$が「1」の時$y$は「400」
同じようにして考えると
$x$が「2」の時$y$は「800」…ですね
⑵「比例の式」覚えてますか?
「算数」では
$y=整数×x$としていましたが
「数学」では
練習問題($x$と$y$の関係を式に表す)

では実際に問題をやっていきましょう
- 「$y$は$x$に比例し〜」→$y=ax$を用意
- $x$と$y$を「代入」して$a$を求める
「比例定数」は
$a=\frac{y}{x}$でも
求めることができますが
⑶のように$x$や$y$が
「分数」の時は
計算を間違えやすいので
注意しましょうね
座標
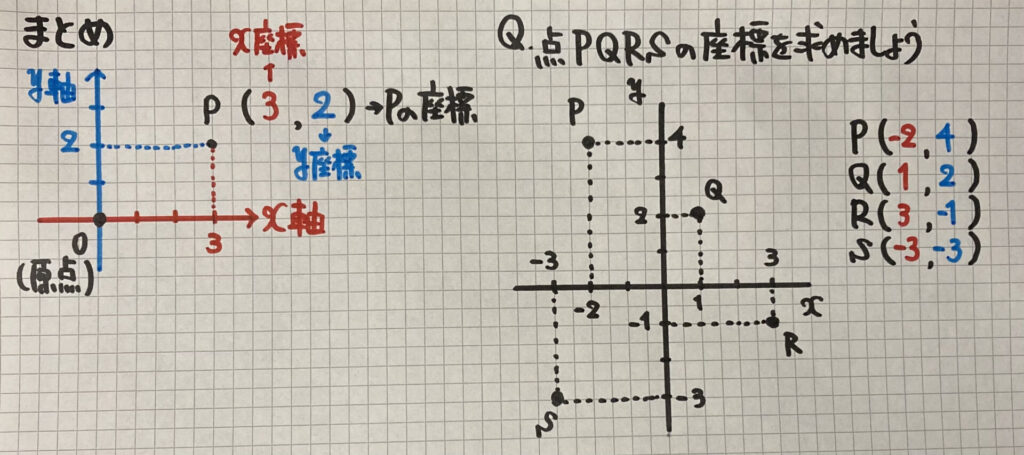
グラフを書くとき
2つの直線を点Oで直角に
交わる数直線を書きます
点Pの位置を(3,2)と表し「座標」と言います
ちなみに原点Oの座標は(0,0)です
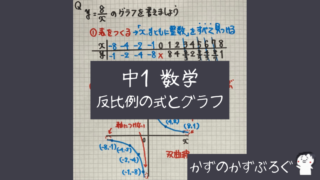
比例のグラフ

まずは「比例のグラフ」の書き方です
- $x$と$y$の表を作る
- 整数の$x$と$y$を見つける
- グラフに、その点をとる
- その点と原点を通る「直線」を引く
次に「比例のグラフ」の特ちょうです
練習問題(グラフの書き方・式の求め方)

⑵は$x$と$y$が
どちらも「整数」になる
$x=3$まで代入して
(3,2)を見つけましょう
⑶⑷は
「グラフから式を求める」問題です
点の$x$座標$y$座標を
$y=ax$の$x$と$y$に
それぞれ代入して
$a$を求めましょう
⑷のように
座標が「分数」の時は
気をつけましょうね
比例の式とグラフのまとめ

・関数
ともなって変わる2つの変数
$x$と$y$があって
$x$の値が決まると
それに対応して$y$の値が
ただ一つに決まるとき
「$y$は$x$の関数である」という
・変域
「変数($x$や$y$)の
とる値の範囲のこと」
(例)$x$の変域が0以上5未満
0≦$x$<5【不等号を使う】
<「より大きい(小さい)未満」
≦…「以上、以下」
「以(い)」は「=(イ)コール」で
覚えましょう
・比例の式の求め方
$y=a×x$
$a$は「比例定数」
$a=\frac{y}{x}=y÷x$で
求めることができる
・比例の式の問題の解き方
- 「$y$は$x$に比例し〜」→$y=ax$を用意
- $x$と$y$を「代入」して$a$を求める
・座標
A$(a,b)$の
$a$を$x$座標 $b$を$y$座標
・比例のグラフの書き方
- $x$と$y$の表を作る
- 整数の$x$と$y$を見つける
- グラフに、その点をとる
- その点と原点を通る「直線」を引く
・比例のグラフの特徴
原点を通る直線になる
$a$(比例定数)が
$a$>0(正の数)の時「右上がり」
$a$<0(負の数)の時「右下がり」
$a$(比例定数)が
「大きい」と「傾きが急」になる
以上、「数学嫌いな人が、
数学を楽しく好きになって欲しい」
かずのかずぶろぐでした