今回は
「平面」と「直線」の
関係の問題です
「算数」で学習した
「垂直」「平行」が
出てきます
問題を解く時に
「立方体」で考えると
分かりやすいので
「立方体」を
早く書けるようにしておく
ことも重要ですよ
では、一緒にやっていきましょう
平面の決定
一番簡単な図形は
何か分かりますか?
それは「点」です
その「点が2つ」になると
「線分」になりますね
では「点が3つ」になると…
「面」を表すことができるようになります
ここでは
その「面」を
「平面」と呼んでいます
もちろん「数学」ですから
「限りなく」
書くことはできません
ただ、頭の中では
「限りなく」あると
考えましょう
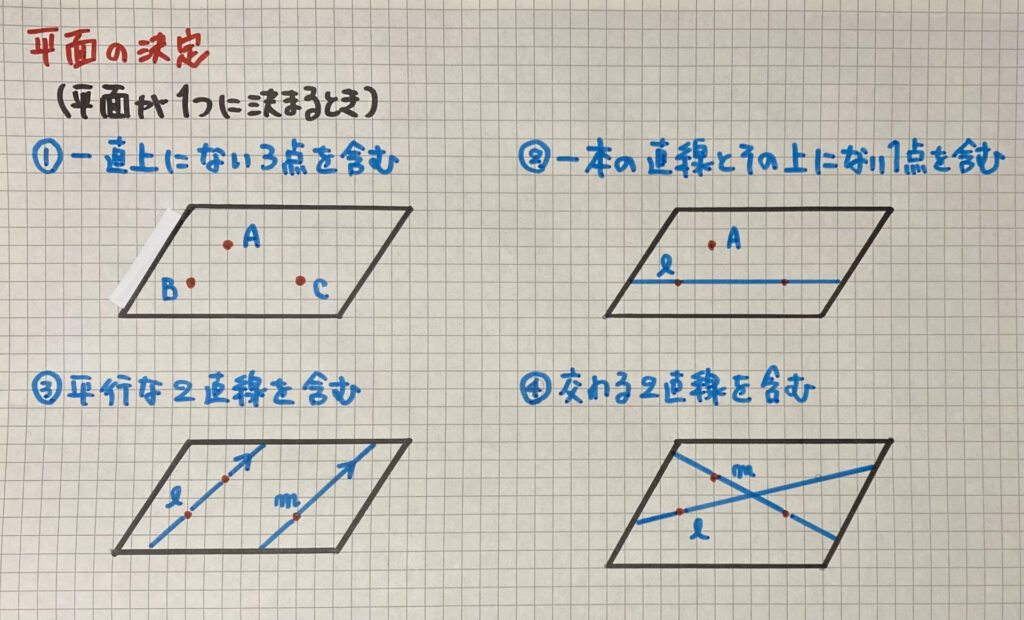
- 一直線上にない3点を含む面(ちなみに一直線上の3点は直線ですね)
- 一本の直線とその上にない1点を含む面
- 平行な2直線を含む面
- 交わる(垂直な)2直線を含む面
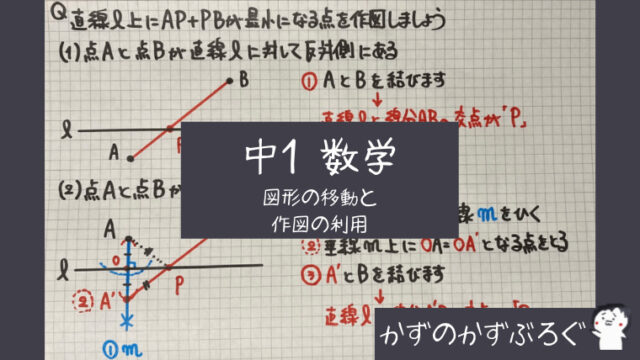
ノートを見てもらうと
分かりやすいと思うのですが
①の点3つ(A B C)が
基本の考え方になります
②の直線は
「点B Cを通っている」
③の2直線は
ℓが「点A Bを通っている」
mは「点C を通り直線ABに平行」
④の直線は
mが「点A Cを通っている」
ℓは「点Bを通る直線」
と見ることもできます

ちょっと説明が長くなりましたね…
ノートのまま
「平面の決定は4種類ある」
それぞれをしっかり
覚えてくれれば大丈夫です
2直線の位置関係

次に
「2直線の関係」です
3種類あります
- 交わる(90°だと垂直)
- 平行
- ねじれの位置
「交わる」と「平行」は
大丈夫ですよね
新しく出てきたのが
「ねじれの位置」です
難しそうに見えますが
次のやり方を
おさえると簡単にできます
- 交わる直線に印をする
- 平行な直線に印をする
- 印の入っていないものが「ねじれの位置」です
①と②は反対でも大丈夫です
ノートにも
辺に印を入れているので
図形と問題をよく見て
解いていきましょう
直線と平面の位置関係
次は
「直線と平面の位置関係」です
3種類あります
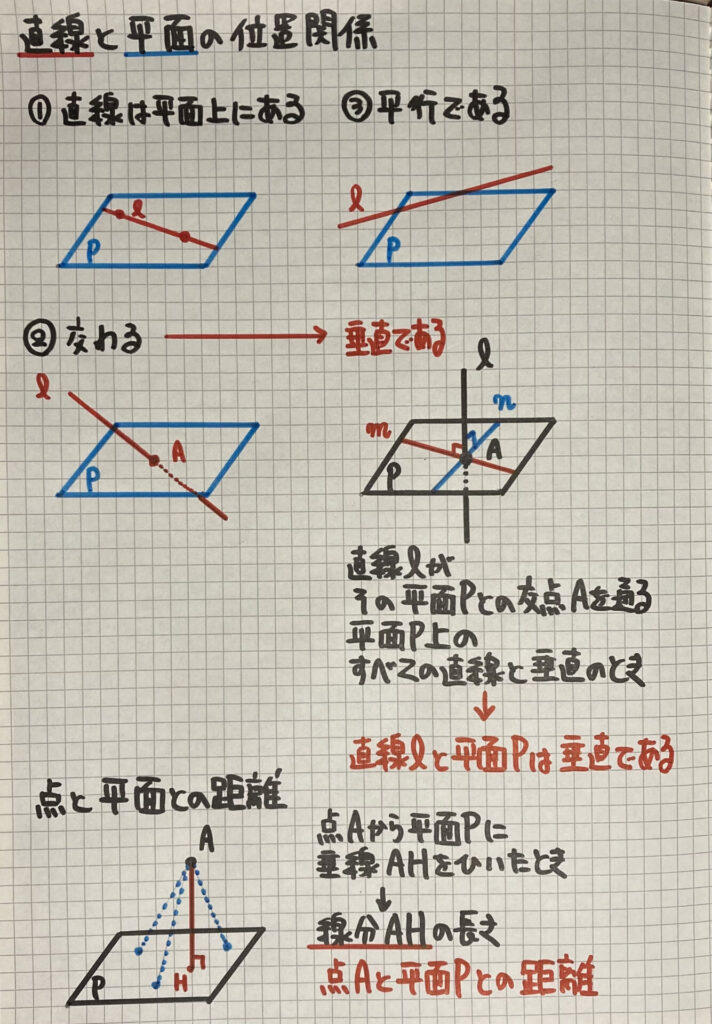
- 直線は平面上にある
- 交わる
- 平行である
②の「交わる」関係を
少し詳しく見ていきましょう
「垂直になる時」ですが
ノートには2本しか
書いていませんが
「平面上の全ての直線」と
「垂直」にならないと
直線ℓと平面Pは垂直にならないです
自分で鉛筆やペンを使って
確かめてみても
分かりやすいと
思いますよ
点と平面の距離
ノートの下にあるように
「数学」の「距離」は
「最短距離」(一番短い距離)
のことです
練習問題
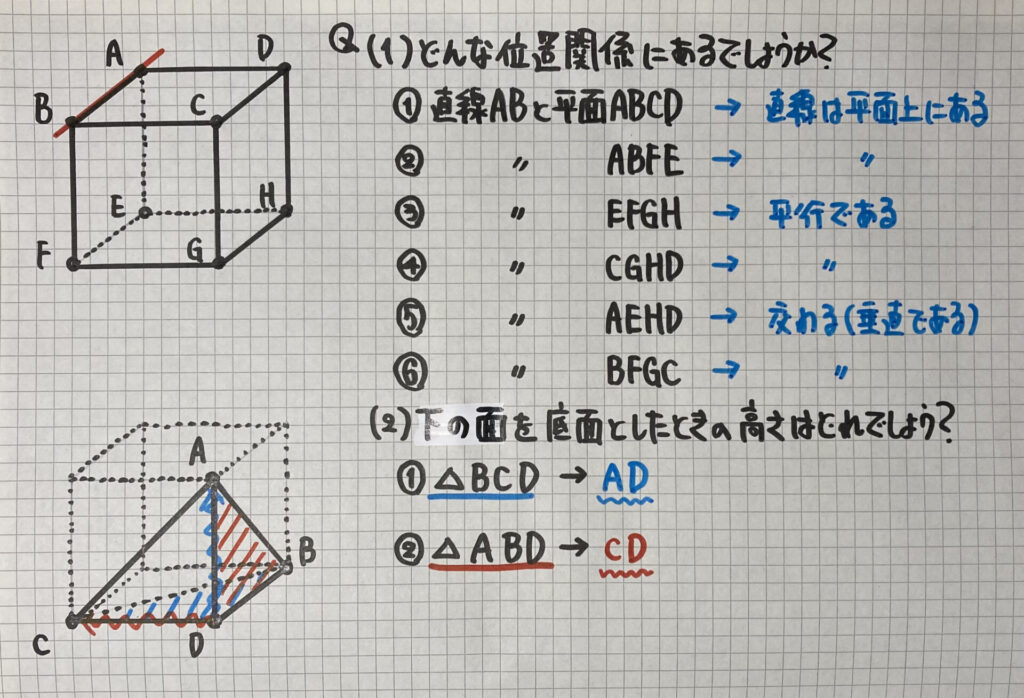
⑴は
直線ABとあるので
立方体の辺ABを
伸ばして考えましょう
⑵の三角錐ですが
「高さ=最短経路=垂線」
となりますね
図では
「90°に見えないこと」が
よくあるので
気をつけましょう
2つの平面の位置関係
最後は
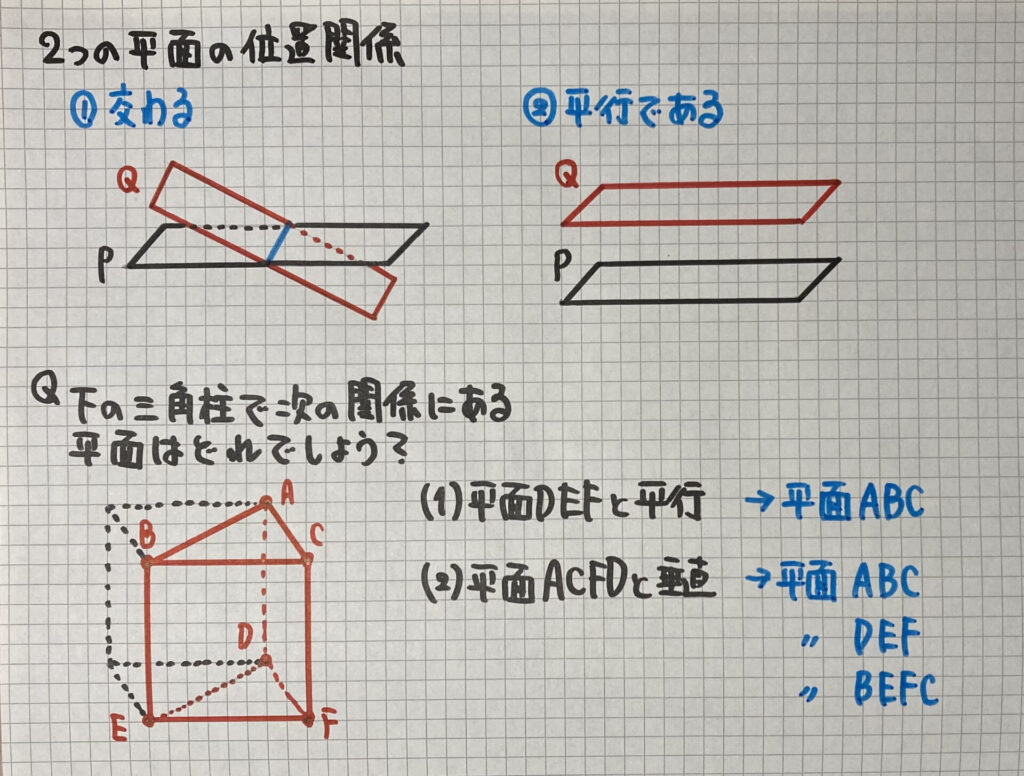
「2つの平面の位置関係」です
2種類あります
- 交わる
- 平行である
ノートでしっかり
確認したくださいね
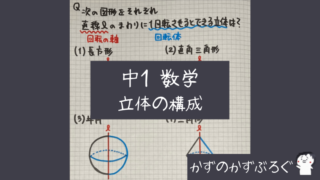
練習問題
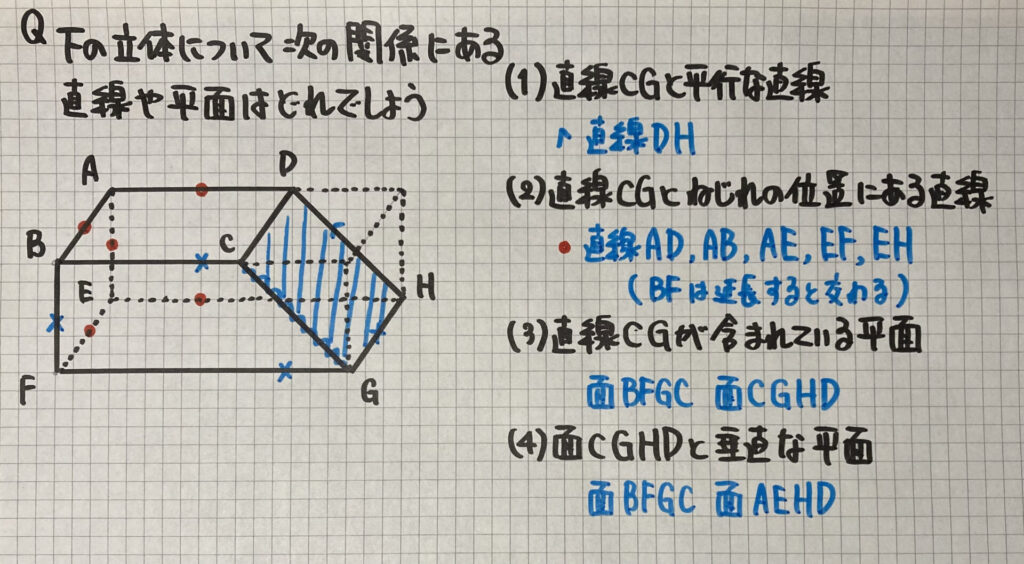
直方体から三角柱を切り取った
「立体」の問題です
面CGHDが斜めになっているので
気をつけましょう
⑵では
辺BFは直線CGと
「平行でなく」
「交わらない」ように
見えますが
「直線」BFなので
伸ばして考えます
- BFを「上に伸ばす」
- CGを「左上に伸ばす」と
交わるので
「ねじれの位置」には
なりませんね
空間内の平面と直線のまとめ

・平面
平に限りなく広がっている面のこと
・平面の決定
- 一直線上にない3点を含む面(ちなみに一直線上の3点は直線ですね)
- 一本の直線とその上にない1点を含む面
- 平行な2直線を含む面
- 交わる(垂直な)2直線を含む面
・2直線の位置関係
- 交わる(90°だと垂直)
- 平行
- ねじれの位置
・ねじれの位置
空間内の2直線が
平行でなく交わらない時の
2直線の関係のこと
「交わる」「平行」以外が
「ねじれの位置」になります
・直線と平面の位置関係
- 直線は平面上にある
- 交わる
- 平行である
・点と平面の距離
点と平面の距離は
点から平面に垂線を引いた時の
垂線(線分)の長さのことです
・2つの平面の位置関係
- 交わる
- 平行である
以上、「数学嫌いな人が、
数学を楽しく好きになって欲しい」
かずのかずぶろぐでした