今回は
「面」や「直線」を
ある条件によって動かすとき
どのような
「立体図形」ができるかを
学習します
では、一緒にやっていきましょう
面を回転させてできる図形
まずは、言葉の説明です
回転体の書き方
- 回転の軸に対称な図形を書く
- 対応する点を曲線で結びます
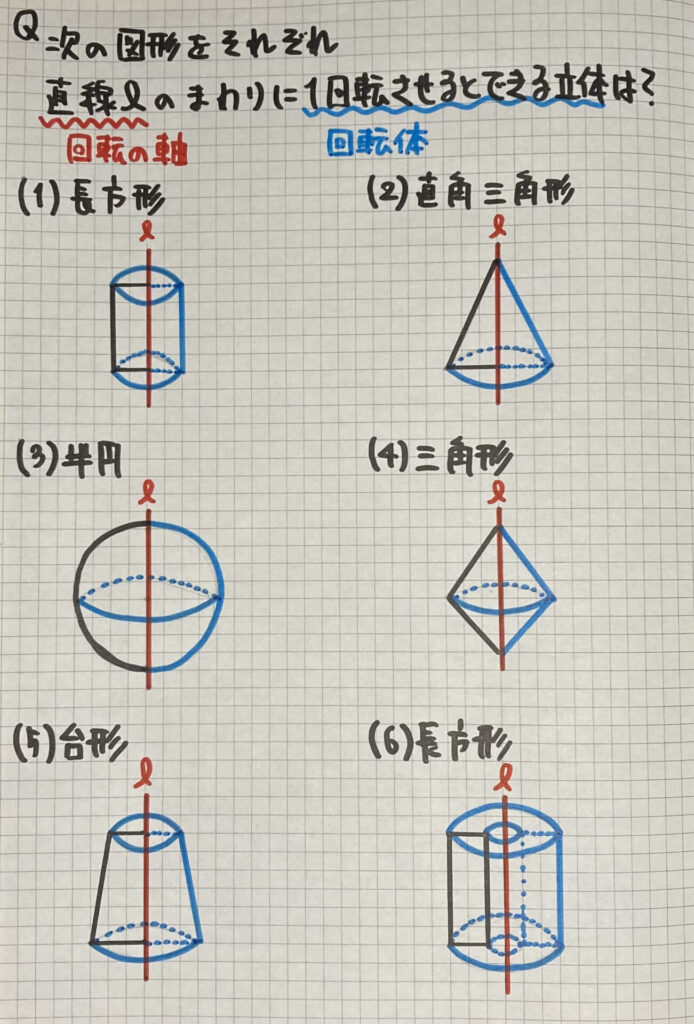
ノートの図形です
(1)長方形→円柱
(2)直角三角形→円錐
(3)半円→球
(4)三角形→円錐を上下に合わせた図形
(5)台形→円錐台(円錐を底面と平行に切ったものです)
(6)軸から離れた長方形→中が空洞な円柱
(5)(6)は
初めて見る人も
いるかと思いますので
一度、見ながらで良いので
書いてみましょう
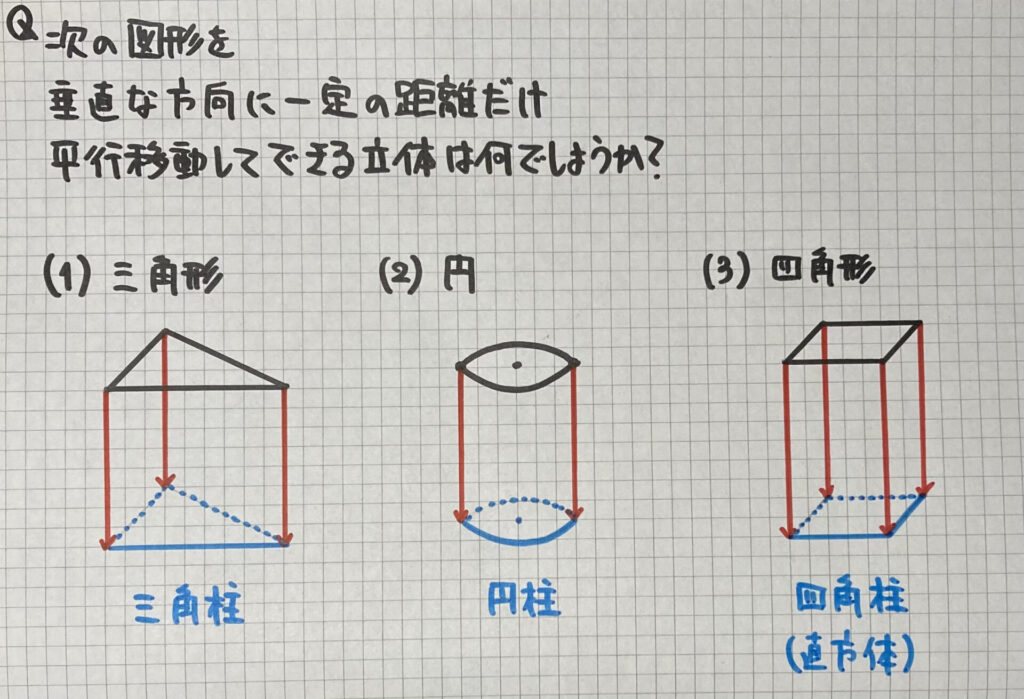
線分を動かしてできる図形
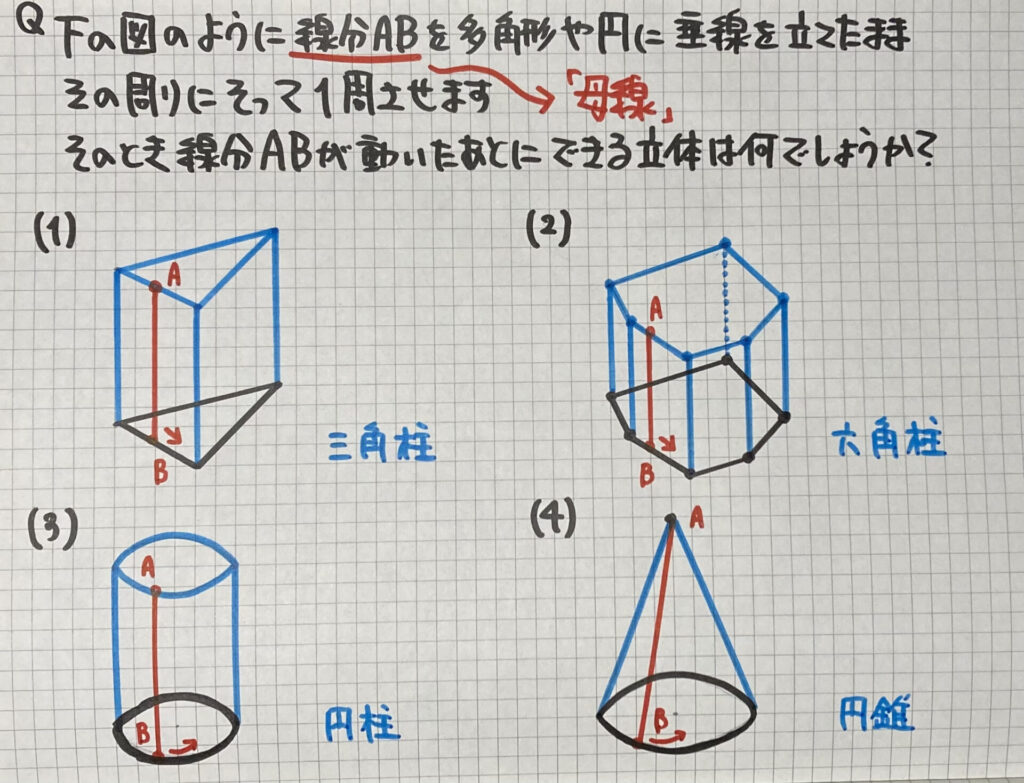
(1)(2)(3)は
移動させた図形が「底面」
線分ABの長さが「高さ」の
柱体になります
(4)は線分を
「垂直ではなく」
点Aに固定して移動しています
これらの図形の
線分ABを
「母線(ぼせん)」
と言います
立体の構成のまとめ

・面や線分を動かしてできる立体
- 面を平行移動してできる図形
- 面を回転させてできる図形
- 線分を動かしてできる図形
・回転体
平面図形を
その平面上の直線ℓのまわりに
1回転させてできる立体のこと
(直線ℓを「回転の軸」といいます)
・回転体の書き方
- 回転の軸に対称な図形を書く
- 対応する点を曲線で結びます
かずのかず
以上、「数学嫌いな人が、
数学を楽しく好きになって欲しい」
かずのかずぶろぐでした