前回、前々回で
図形の「移動」と「作図」を
学習しました
ここでは
「作図」を使った問題を
中心に一緒に見ていきましょう
ノートに「作図」の方法は
ありますが
「作図」の
詳しいやり方は
こちらで確認してくださいね
2点の最短距離

テストでもよく出る
「最短距離」の問題です
(1)は簡単なので
出ることはありませんが
(2)を考える時の
役に立つので
まとめました
まず
「最短距離」ですが
「一番短くなる線分」
のことです
「一番速く行くことができる道」
のようなものです
2つ(2点)の「最短距離」ですが
(1)にあるように
真っ直ぐ(一直線)に結ぶのが
一番短くなりますよね
(2)も同じ考え方です
でも、Pが
ℓ上にあるから
AとBを結べないよ
そうですね
実は
この問題のポイントは
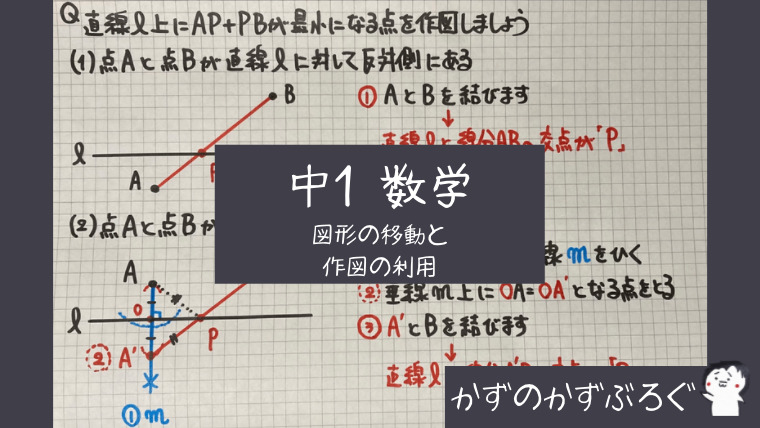
「Aを移動させる」
ことなんです
- Aを(ℓを対称の軸として)対称移動させてA’を作る
- A’とBを結ぶ
- 直線ℓと線分A’Bの交点が「P』
新しくスタート地点(A’)を
ℓの反対側に作るイメージですね
「どうしてこうなるんだろう?」
と思いますよね
次のノートを見てください
別の解き方と説明

実は
Bを移動させても
同じようにPを作図することができます
そして
「なぜ最短になるか」
ですが
まとめました
一度読んだだけでは
難しく感じるかもしれません
一番注目してほしい所は
「赤の点線」と「青の折れ線」は
「どちらが短くなりますか?」
もちろん
直線の「赤の点線」ですよね
ここまで大丈夫でしょうか

もうちょっとですよ
これらのことから
どうでしょうか
「言葉では分かりにくい」
という人は
「赤いP」と
「その他の青いP」を
見比べて考えて見てくださいね
練習問題

先ほどの
「2点の最短経路」
の考え方を使った問題です
家の地点を「A」
学校の地点を「B」
として考えましょう
ここの問題のポイントは
CDは「橋の長さ」なので
必ず必要な「長さ」ですね
次に
家から見ると
A’C=ADとなるので
A’C +CB=AD +CB
が最短になりますね
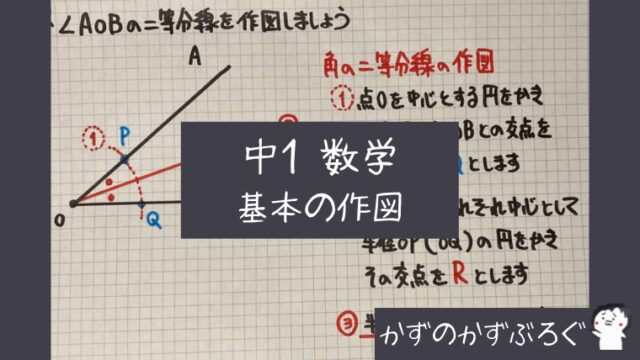
角度の作図
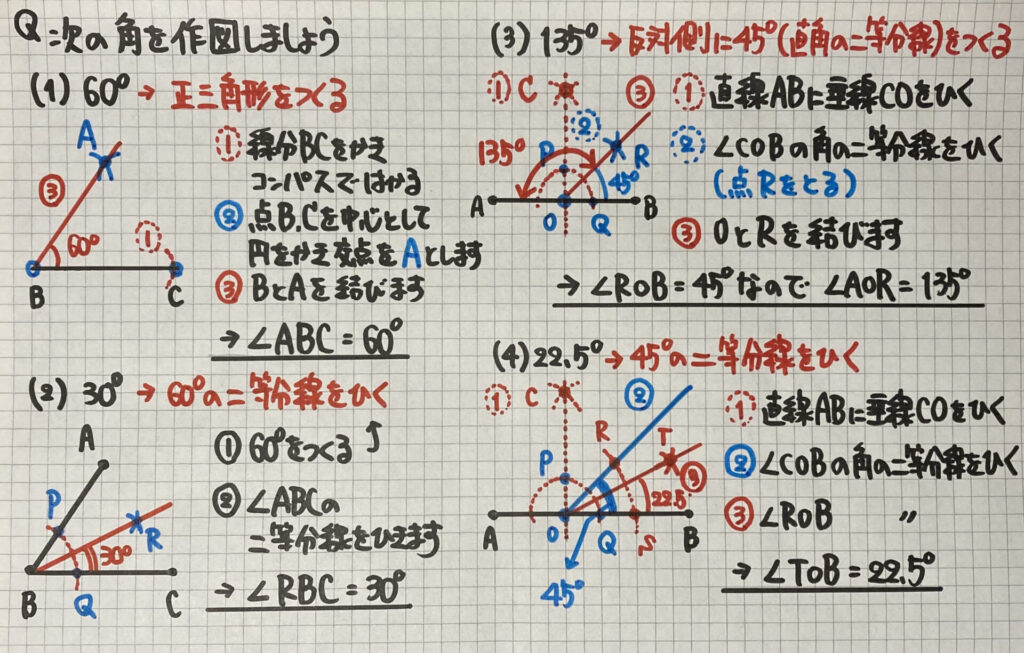
次は
「角度の作図」です
簡単に作図できるのは
この2つ
- 90°…垂線です
- 60°…正三角形の角度です
これらを
二等分していくと
- 90°→45°→22.5°
- 60°→30°→15°
が作図できます
あとは
これらを組み合わせれば
いろんな角度を
作ることができますよ
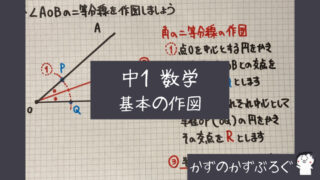
一直線上にある角の二等分線
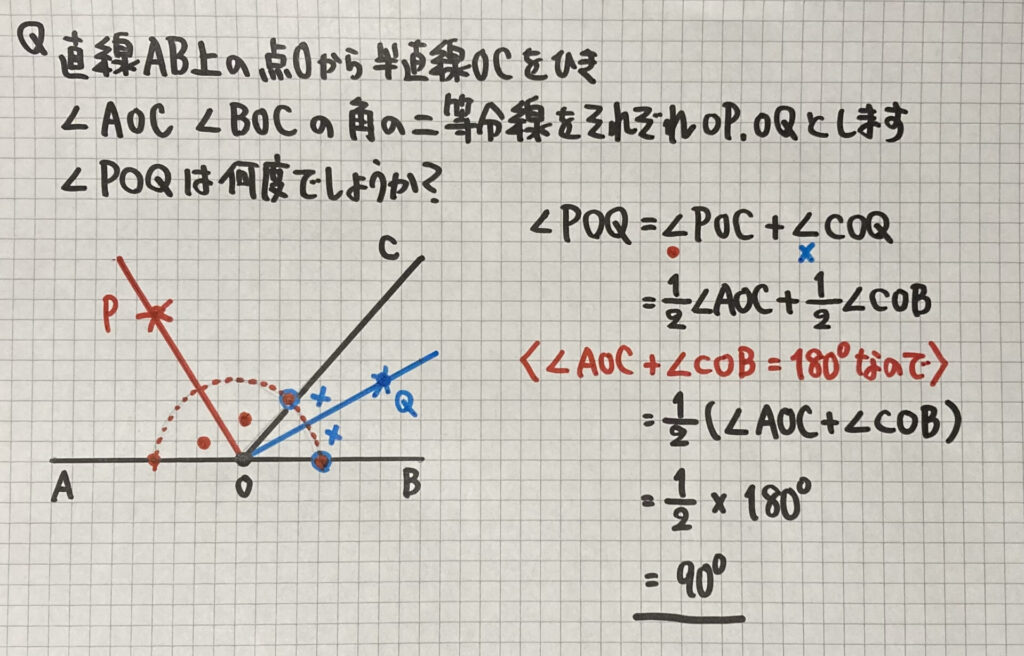
「角の二等分線」の
有名な問題です
知っていれば
見た瞬間に答えを
出すことができますよ
学校のテストで
ノートの右側の
「式を書かせる」問題が
出ることもあるので
見ながらで良いので
一度、自分でも
式を書いて見ましょう
図形の移動と作図の利用のまとめ

・直線ℓ上に
AP +PBが
最小になる点Pの作図
A(もしくはB)を
ℓを対称の軸として
「対称移動」させて
A’(B’)を作り
A`とB(AとB’)を結ぶ
直線ℓと線分A’B
の交点が「P」
・作図できる角度
- 90°…垂線です
- 60°…正三角形の角度です
これらの角の二等分線を作図していくと
- 90°→45°→22.5°
- 60°→30°→15°
を作図することができる
これらを組み合わせて
いろんな角度を作図する
今回は
言葉で説明すると
逆に難しく感じて
しまうことがあるので
ノートをしっかり
見てくださいね
以上、「数学嫌いな人が、
数学を楽しく好きになって欲しい」
かずのかずぶろぐでした