
前回、「方程式とその解」で
「方程式」を勉強しました
「方程式とその解」については

こちらで確認してくださいね
今回は「方程式」を
「より早く簡単に解く方法」
について一緒に見ていきましょう
移項(いこう)のやり方
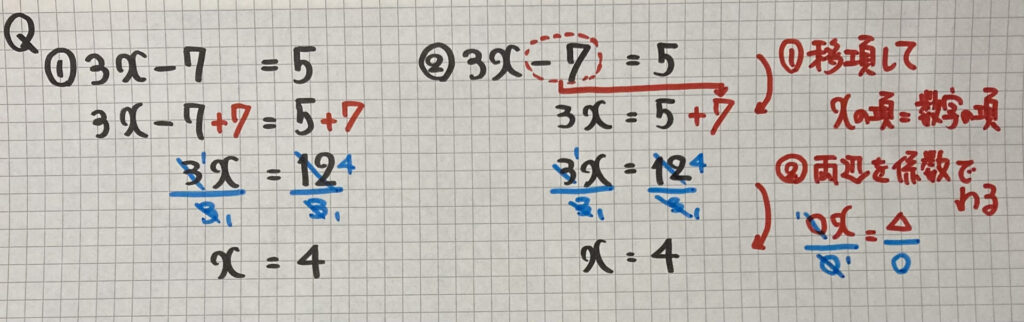
①は前回使った
「等式の性質」を使った
解き方です
両辺に「+7」をして
左辺の「−7」を消しています
見方を変えると
左辺の「−7」が右辺に
移動した様に
考えることができます
これを移項と言います
②では「移項」を使った
解き方です
練習問題

⑵⑷のように
「−で割るとき」
符号に気をつけましょう
⑸⑹のように
$x$の項を左辺に
数字の項(定数項)を右辺に
「移項」でまとめています
このように
「移項」して整理すると
$ax=b$の形になる「方程式」を
「一次方程式」といいます
( )の方程式

- ( )を外す<計算する>
- 「$x$の項」を左辺に「数字の項」を右辺に移項
- 左辺、右辺を計算<簡単に>する
- $ax=b$の式の両辺を$a$で割る
解き方に慣れてくれば
- 青字で書いた<>の式
- 両辺を最後に割る時の数字を書くこと
を省略(頭の中で)しても大丈夫です
分数の方程式
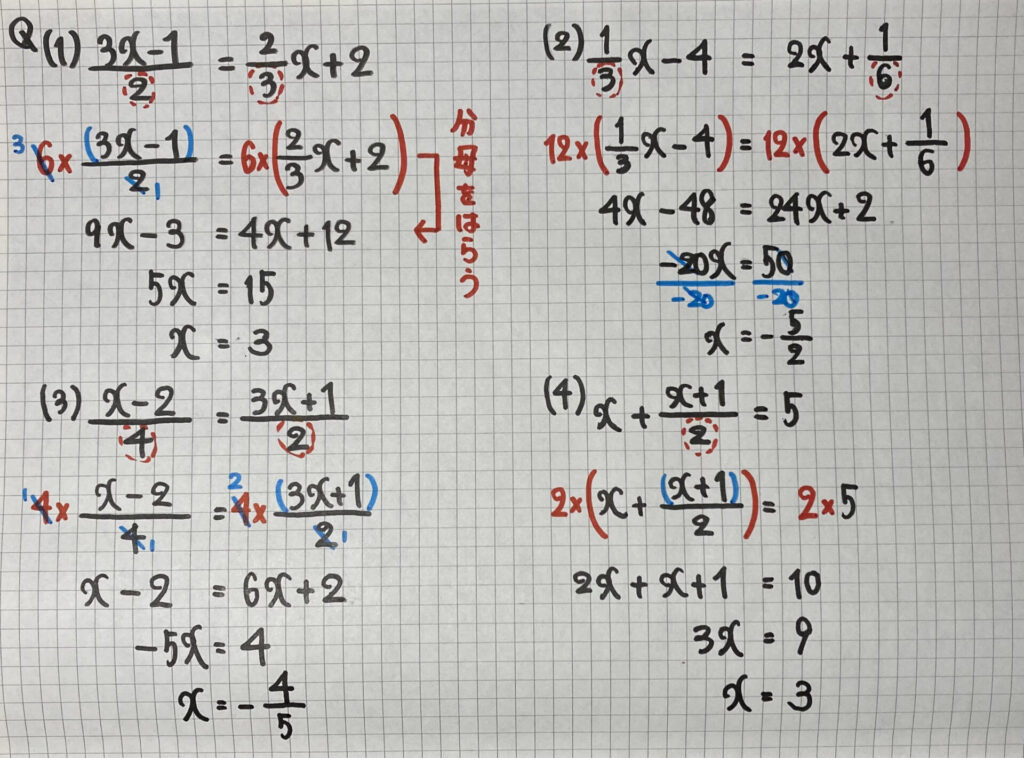
- 「分母の最小公倍数」を両辺にかける
- ( )を外す<計算する>
- 「$x$の項」を左辺に「数字の項」を右辺に移項
- 左辺、右辺を計算<簡単に>する
- $ax=b$の式の両辺を$a$で割る
やり方の①を
少し細かく見ます
分数のままでも
方程式を解くことはできます
しかし、
ミスが多くなるので
まず、「分数の式」を
「整数だけの式」にします
「分母をはらう」といいます
小数の方程式

- 両辺に10(100)倍して両辺を整数の式に
- ( )を外す<計算する>
- 「$x$の項」を左辺に「数字の項」を右辺に移項
- 左辺、右辺を計算<簡単に>する
- $ax=b$の式の両辺を$a$で割る
解き方に慣れてくれば
- 青字で書いた<>の式
- 両辺を最後に割る時の数字を書くこと
を省略(頭の中で)しても大丈夫です
⑴は小数第一位までの
小数しかないので
「両辺を10倍」しています
⑵は考え方を逆に使っています
両辺の係数を見ると
「300」「1200」で
「100で割ること」ができます
さらに「3で割ること」ができる
つまり「300で割ること」ができます
もちろん割らずに計算して
解くことも可能です
「もし、気がつけば…」ぐらいで
大丈夫です

⑶は小数第二位までの
小数があるので
「両辺を100倍」しています
⑷は「両辺を10倍」していますが
「0.5」「−0.2(7$x$−2)」「0.1」
「全ての項」に「10をかける」のを
忘れないようにしましょう
方程式の解き方(移項)のまとめ

・移項
等式で、左辺(右辺)の項を
符号を変えて
右辺(左辺)に移すこと
・一次方程式
$ax=b$の形になる「方程式」
・移項を使った解き方
- 「$x$の項」を左辺に「数字の項」を右辺に移項
- 左辺、右辺を計算<簡単に>する
- $ax=b$の式の両辺を$a$で割る
・( )の式の解き方
( )を外す<計算する>
その後は
- 「$x$の項」を左辺に「数字の項」を右辺に移項
- 左辺、右辺を計算<簡単に>する
- $ax=b$の式の両辺を$a$で割る
・分数の式の解き方
「分母の最小公倍数」を両辺にかける<分母を払う>
その後は
- 「$x$の項」を左辺に「数字の項」を右辺に移項
- 左辺、右辺を計算<簡単に>する
- $ax=b$の式の両辺を$a$で割る
・小数の式の解き方
両辺に10(100)倍して両辺を整数の式に
その後は
- 「$x$の項」を左辺に「数字の項」を右辺に移項
- 左辺、右辺を計算<簡単に>する
- $ax=b$の式の両辺を$a$で割る
以上、「数学嫌いな人が、
数学を楽しく好きになって欲しい」
かずのかずぶろぐでした







