前回
「平行四辺形」の
「定義」「性質」
について学習しました
かずのかず
こちらで
確認してくださいね
【中2数学】「平行四辺形の性質」の問題 どこよりも簡単な解き方・求め方前回まで、いろいろな「三角形」について学習してきました 今回からは「四角形」について学習していきます まずは「平行四辺形」です 算数でも「面積」「対称な図形」で学習しましたね もう少し図形について詳しく一緒に見ていきましょう...
今回は
平行四辺形に
「なるための条件」
について一緒に
見ていきましょう
平行四辺形になるための条件

「平行四辺形になるための条件」
は「5つ」あります
ノートにまとめましたが
こちらでも
まとめますね
平行四辺形になるための条件
- 2組の向かいあう辺が、それぞれ平行であるとき(定義)
- 2組の向かいあう辺が、それぞれ等しいとき
- 2組の向かいあう角が、それぞれ等しいとき
- 対角線が、それぞれの中点で交わるとき
- 1組の向かいあう辺が、等しくて平行であるとき
①は前回、学習した「定義」です
「5つ」全てを覚えるのは
少し大変ですが
問題を解きながら
覚えていきましょう
「平行四辺形であること」の証明①
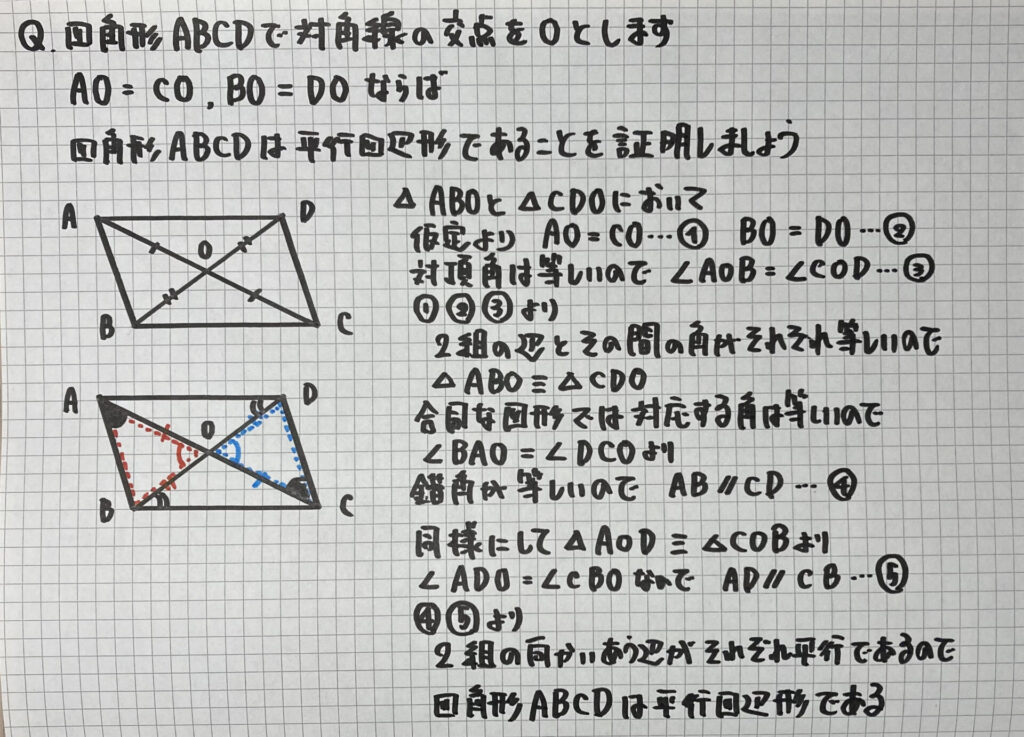
「①2組の向かいあう辺がそれぞれ平行であるとき(定義)」
を利用した証明です
三角形の合同を証明
↓
対応する角(錯角)が等しい
↓
辺が平行である
この流れで
証明することが
できました
「平行四辺形であること」の証明②
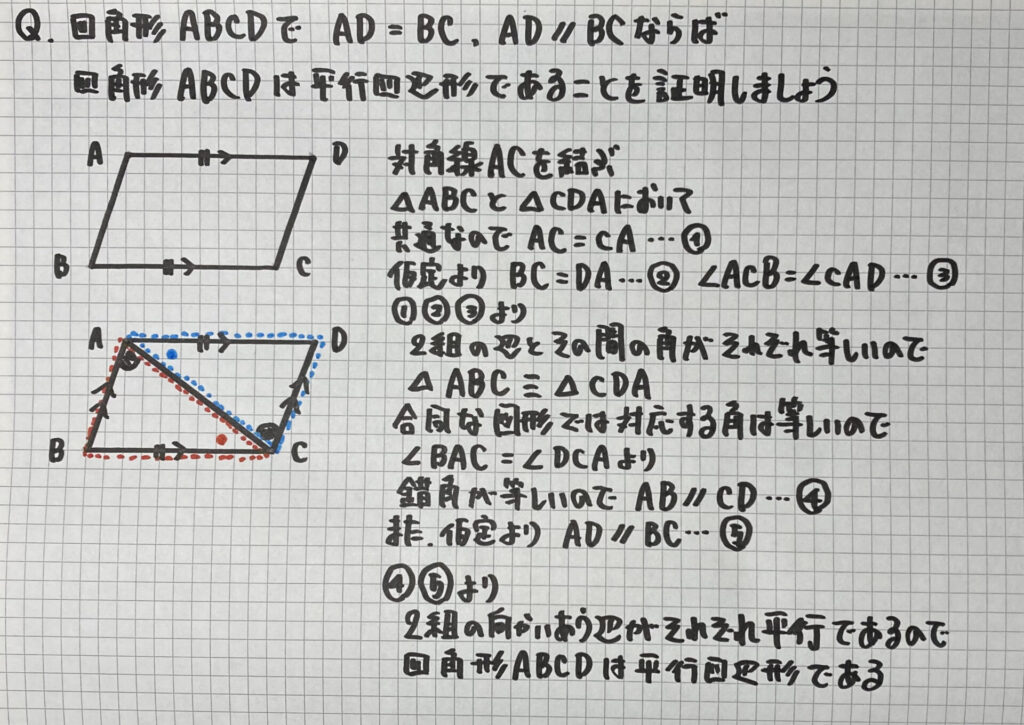
この問題も
「①2組の向かいあう辺がそれぞれ平行であるとき(定義)」
を利用した証明ですが
自分で三角形を作っていますので
「対角線ACを結ぶ」からスタートします
あとの流れは
先ほどの問題と同じです
「平行四辺形であること」の証明③
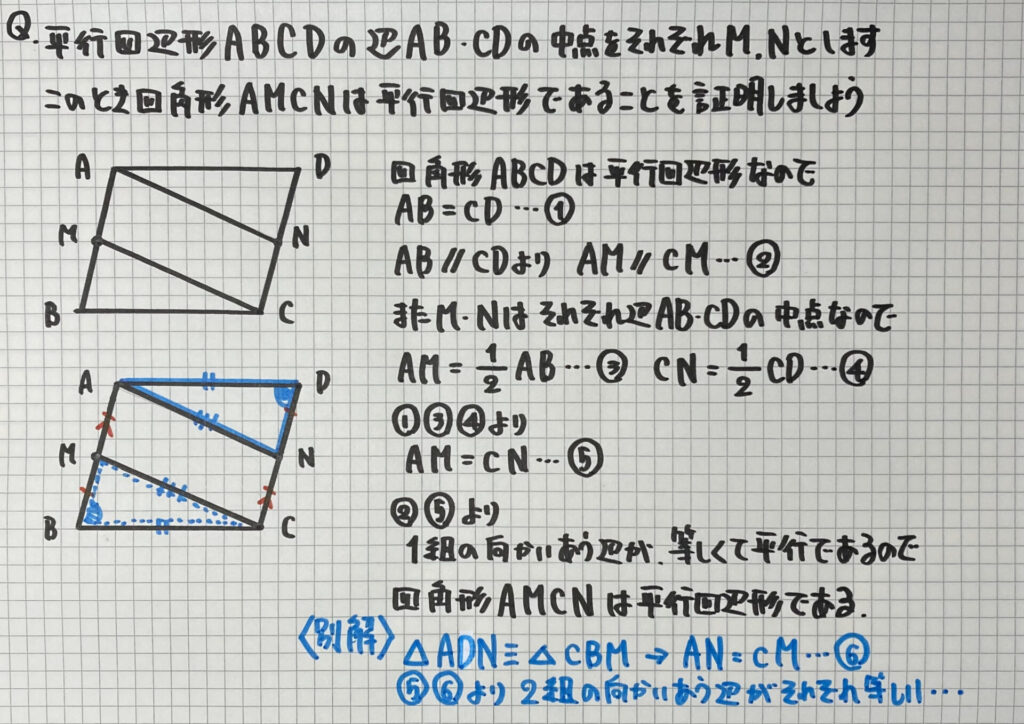
今回は
2つの方法
「⑤1組の向かいあう辺が等しくて平行であるとき」
「②2組の向かいあう辺がそれぞれ等しいとき」
で「証明」をすることができます
ノートには
「⑤の条件」を
利用しています
この問題のポイントは
①③④の等式を使って
⑤の等式を作ることです
平行四辺形の中にある
「平行四辺形」を証明しています
「②の条件」を
利用する場合は
△ADNと△CBMの合同を証明する
↓
対応する辺の長さは等しいので
AN=CM
↓
(ノートの証明より)
AM=CN
この流れで
証明をすることが
できます
平行四辺形になるための条件のまとめ

・平行四辺形になるための条件
- 2組の向かいあう辺が、それぞれ平行であるとき(定義)
- 2組の向かいあう辺が、それぞれ等しいとき
- 2組の向かいあう角が、それぞれ等しいとき
- 対角線が、それぞれの中点で交わるとき
- 1組の向かいあう辺が、等しくて平行であるとき
・平行四辺形の証明
対角線をひき
「1組の三角形」を作る
かずのかず
以上、「数学嫌いな人が、
数学を楽しく好きになって欲しい」
かずのかずぶろぐでした