前回学習した
「一次関数のグラフ」
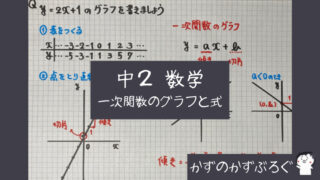
【中2数学】「一次関数のグラフと式」の問題 どこよりも簡単な解き方・求め方今回は一次関数の「グラフと式」です 「グラフの書き方」「変域のグラフ 求め方」「グラフから式を求める」「問題文から式を求める」問題について一緒に見ていきましょう...
の考え方を使って
今回は
「方程式とグラフ」について
一緒に学習して
いきましょう
$ax+by=c$型のグラフ

$ax+by=c$型の
グラフの書き方は
2種類あります
- 等式変形で「$y=〜$」の形にする
- 簡単な2点($x=0$と$y=0$)を求める
問題によって
求めやすい方を
使いましょう
軸に平行なグラフ
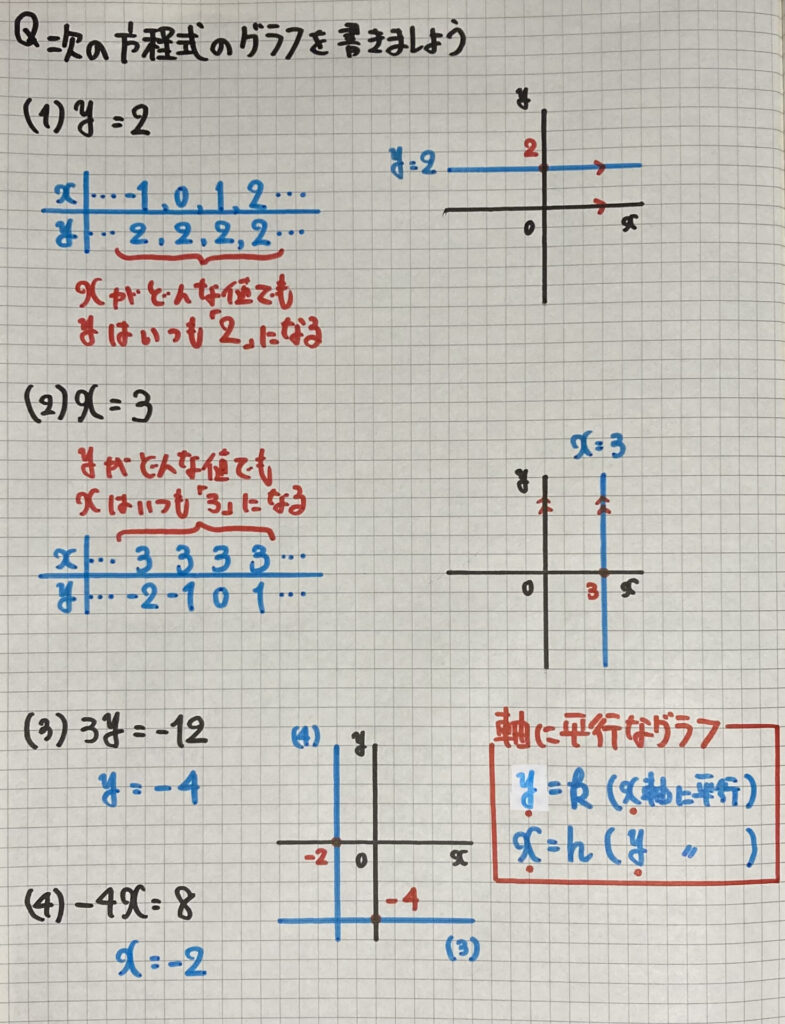
(1)は
$x$がどんな値でも
$y$は、いつも「2」なので
(0,2)を通って
「$x$軸」に
平行な直線になります
(2)は
$y$がどんな値でも
$x$は、いつも「3」なので
(3,0)を通って
「$y$軸」に
平行な直線になります
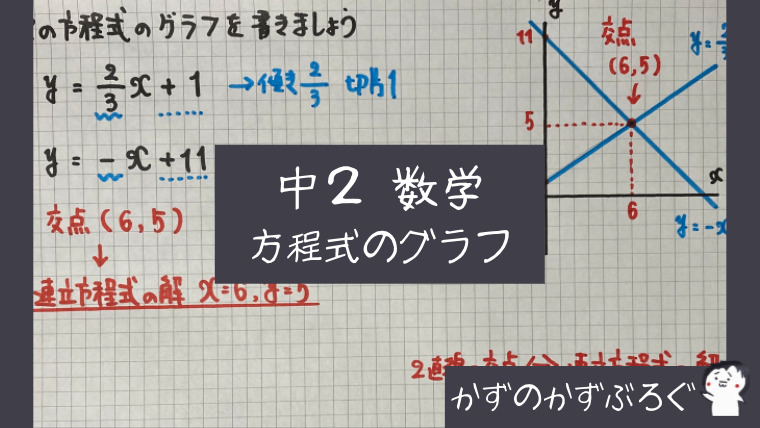
連立方程式とグラフ

まずは
言葉の説明です
交点の(6,5)は
$y=\frac{2}{3}x+1$と
$y=−x+11$
の2つのグラフが
どちらも通っていますね
「グラフが通る点=$x$と$y$が方程式の解になる」
となり
2つの方程式の解→連立方程式の解
となりますね
大切なポイントを
まとめます
方程式のグラフのまとめ

・$ax+by=c$型のグラフの書き方は
- 等式変形で「$y=〜$」の形にする
- 簡単な2点($x=0$と$y=0$)を求める
・軸に平行なグラフ
- $y=k$($x$軸に平行)
- $x=h$($y$軸に平行)
な直線になる
・連立方程式とグラフ
グラフの
2直線の交点(の座標)
=連立方程式の解
かずのかず
以上、「数学嫌いな人が、
数学を楽しく好きになって欲しい」
かずのかずぶろぐでした