前回までで
「平行四辺形」の
「定義」「性質」
「なるための条件」
を学習してきました
かずのかず
こちらで
確認してくださいね
今回は
その他の
「平行四辺形の証明」
を一緒にやっていきましょう
平行四辺形の証明①
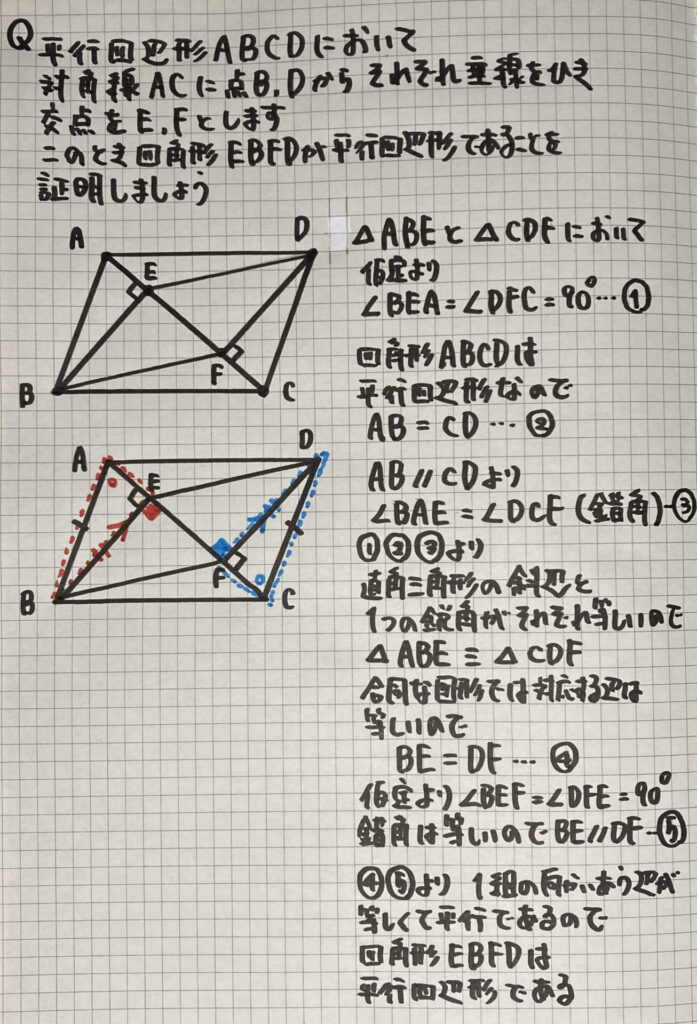
平行四辺形の中に
四角形を作って
その四角形が
「平行四辺形」である
ことを証明する問題です
今まで
学習してきた
2種類の証明を利用して
- 「1組の向かいあう辺が、等しくて平行であるとき」
という
「なるための条件」で
四角形が
平行四辺形であることを
証明することが
できますね
平行四辺形の証明②

三角形の外に
ある辺と平行な直線を引き
その直線上に
ある点から等しい距離の点をとります
三角形の辺上の2点と
外部の直線上にある2点で
四角形を作り
それが「平行四辺形」である
ことを証明する問題です
- 対角線が、それぞれの中点で交わるとき
という
「なるための条件」で
4点で作る四角形が
平行四辺形であることを
証明することが
できました
平行四辺形の証明③
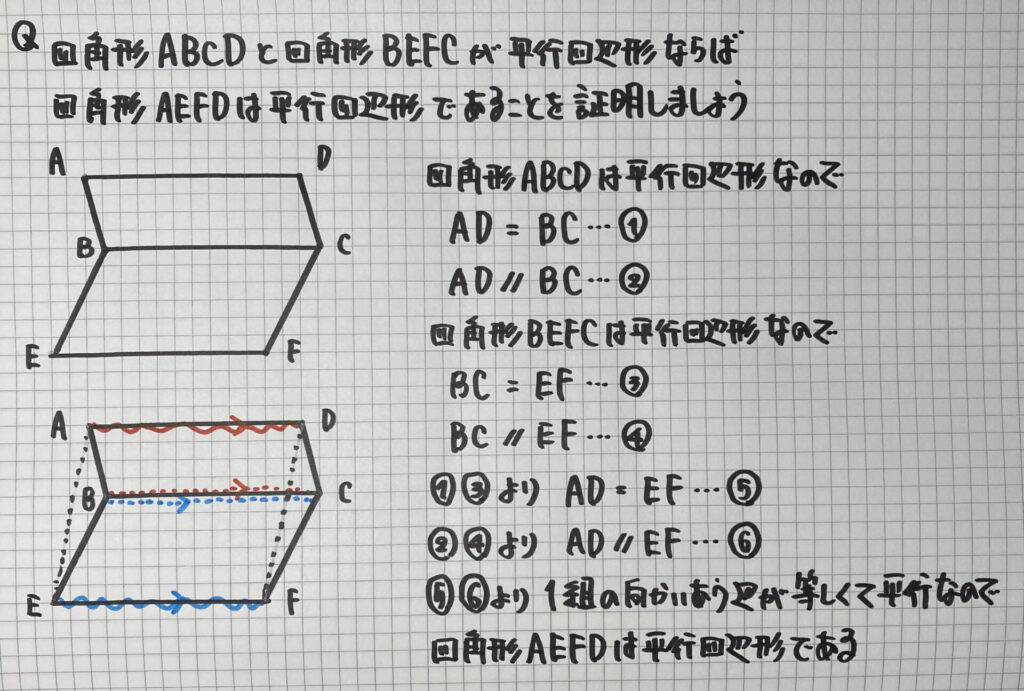
2つの「平行四辺形」の
ある「4点」からできる
四角形が「平行四辺形」である
ことを証明する問題です
この2つの性質を利用して
- 「1組の向かいあう辺が、等しくて平行であるとき」
という
「なるための条件」で
平行四辺形であることを
証明することができます
平行四辺形の証明のまとめ

・平行四辺形の証明で
よく使う流れ
- 「垂線」という「仮定」から
- 2直線の「錯角」が等しい
- 2直線が「平行」であることを証明します
- 「平行四辺形」という「仮定」から
- 三角形の合同を証明して
- 四角形の「辺の長さが等しい」ことを証明します
「仮定」の
- 「平行線」から「錯角が等しい」
- 「等しい長さ」の「辺」
から三角形の合同を証明して
四角形の「対角線が中点で交わる」ことを
証明します
平行四辺形の性質
- 「2組の向かいあう辺がそれぞれ平行な四角形」(定義)
- 「2組の向かいあう辺はそれぞれ等しい」から
「1組の向かいあう辺が、等しくて平行であるとき」の条件を利用します
かずのかず
以上、「数学嫌いな人が、
数学を楽しく好きになって欲しい」
かずのかずぶろぐでした