前回は
「場合の数と確率①」
として
「サイコロ」「色玉」
「整数」について
学習しましたね
かずのかず
こちらで
確認してくださいね

【中2数学】「場合の数と確率①」の問題 どこよりも簡単な解き方・求め方今回は「確率」を学習します 天気予報の「降水確率」やトランプゲームの「出るカードの確率」等で、何となくは知っている人も多いですよね 数学での「確率」は、算数で学習した「並べ方と組合せ方」を利用して「確率」を求めます では、一緒にやっていきましょう...
今回は
「場合の数と確率②」
として
「コイン」「くじ引き」
「じゃんけん」
「図形(サイコロ)」
の問題を
一緒にやっていきましょう
「コインの表裏」の確率

ノートにも
まとめましたが
で考えると
分かりやすいです
「少なくとも…」の問題
は前回もやりましたね
「少なくともAが起こる確率($p$)」の問題
- Aが起こらない確率を求める
- $p$=1−(Aが起こらない確率)で求める
でやってみましょう
「コイン(合計金額)」の問題

先ほどの問題と
やり方は同じです
最後に
「合計金額」を書いて
確率を求めましょう
「くじ引き」の確率

前回やった
「色玉」の問題と同じように
で樹形図を書きます
「同時に2本引いた…」
↓
「組合せ」で考えます
「じゃんけん」の確率
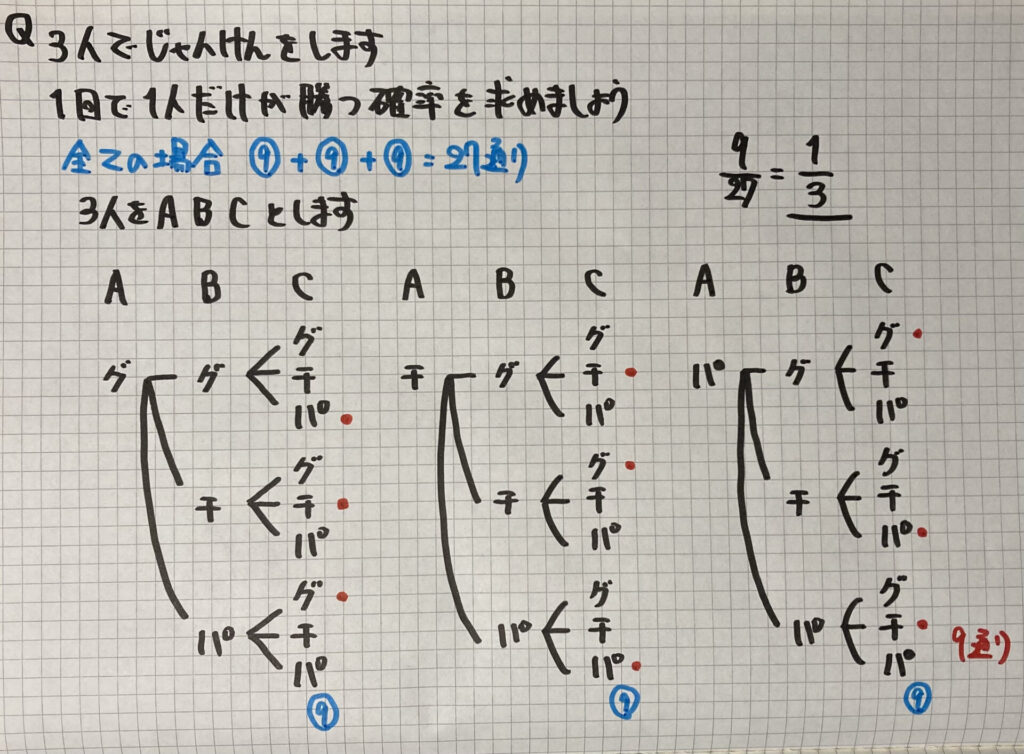
じゃんけんは
1人につき
「グー」「チョキ」「パー」の
3種類があるので
「樹形図」が多くなります
慣れてきたら
全ての場合の数は
計算で求めることができます
ノートでは
「⑨+⑨+⑨=27通り」
としていますが
最初のうちは
しっかり「樹形図」を
書いて練習しましょうね
「図形(サイコロ)」の確率
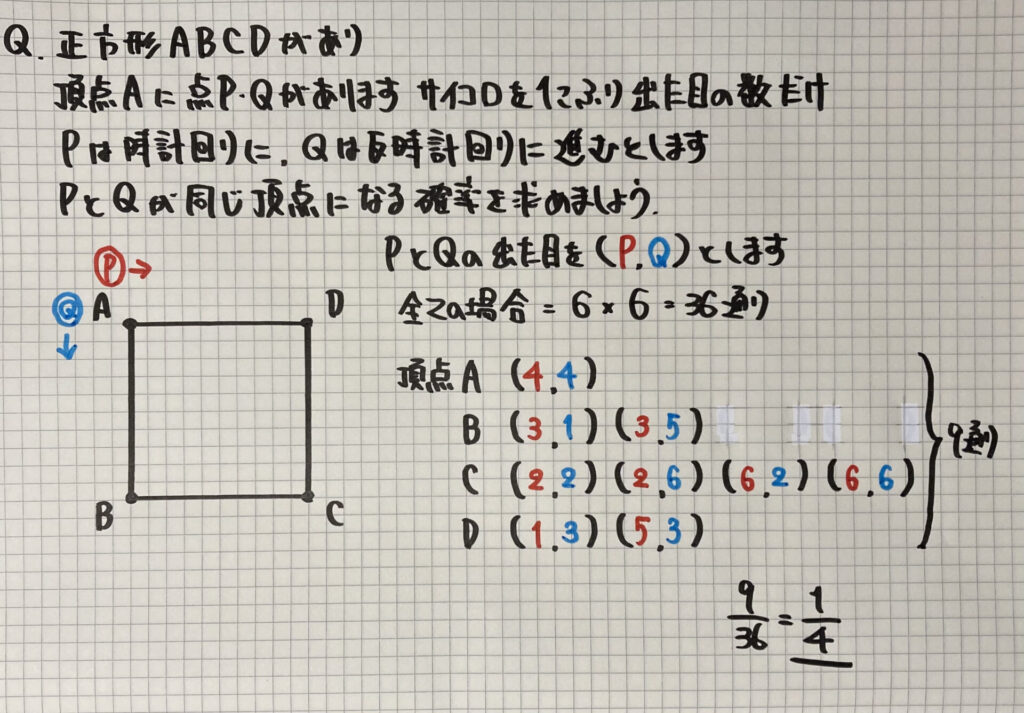
「図形」で
「点が動く」問題です
全ての場合の数は
サイコロが
PとQの「2こ」なので
6×6=36通り です
この問題の
ポイントは
頂点A以外は
P(もしくはQ)が
同じ頂点に「違うサイコロの目」
で止まることがあるので
注意しましょうね
場合の数と確率②のまとめ

・コインの問題
- ABC 等の「名前」をつける
- 表…○ 裏…×として樹形図を書く
・くじ引きの問題
あたり、はずれに「名前」をつけましょう
あたり、はずれに「名前」をつけましょう
例
あたり3こ…○1 ○2 ○3
はずれ2こ…×1 ×2
・じゃんけんの問題
$x$人で
「じゃんけん」をした時
全ての場合の数は
「$3^x$通り」
になります
かずのかず
以上、「数学嫌いな人が、
数学を楽しく好きになって欲しい」
かずのかずぶろぐでした