前回まで
「平行四辺形」
について学習しました
こちらで
確認してくださいね

今回は
「いろいろな四角形」として
「算数」でも学習した
「ひし形・長方形・正方形」
について一緒に
やっていきましょう
いろいろな四角形の性質
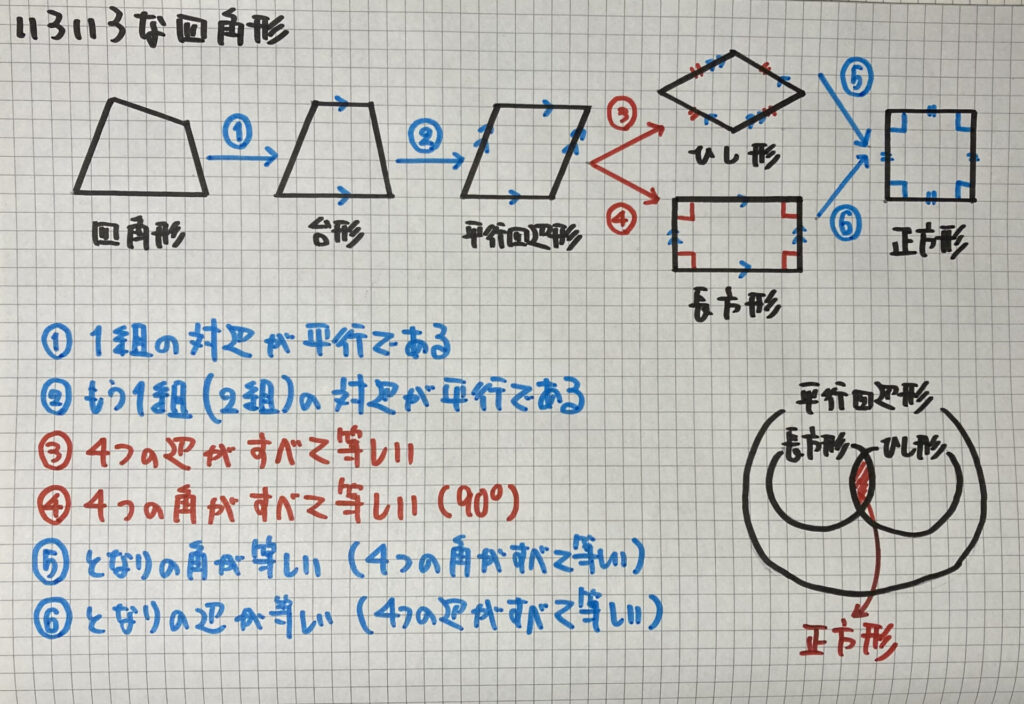
一番左が
「ただの四角形」です
①上下(左右)の1組の辺が平行になると
- 「台形」になります
「台形」の
②左右(上下)のもう1組の辺が平行になると
- 「平行四辺形」になります
「平行四辺形」の
③4つの辺の長さが全て等しくなると
- 「ひし形」になります
④4つの角の大きさが全て等しくなると
- 「長方形」になります
「ひし形」の
⑤となりの角の大きさが等しくなると
(4つの角が全て等しくなると)
- 「正方形」になります
「長方形」の
⑤となりの辺の長さが等しくなると
(4つの辺が全て等しくなると)
- 「正方形」になります
よくノートの
「四角形の流れ」を
確認しておいてください
また
四角形の関係
- 「平行四辺形」
- 「長方形」
- 「ひし形」
- 「正方形」
をノートの右下に
図でまとめていますので
そちらも合わせて
確認しておきましょうね
いろいろな四角形の定義
定義を
まとめておきますね

大丈夫ですか?
全部を一気に覚える
必要はありませんので
安心してください!
では、あと1つだけ
「長方形の対角線の長さが等しい」証明

「長さ」が等しい証明は
先ほど
を学習しましたね
あとは
ノートの流れを
しっかり確認してください
「ひし形の対角線が垂直に交わる」証明
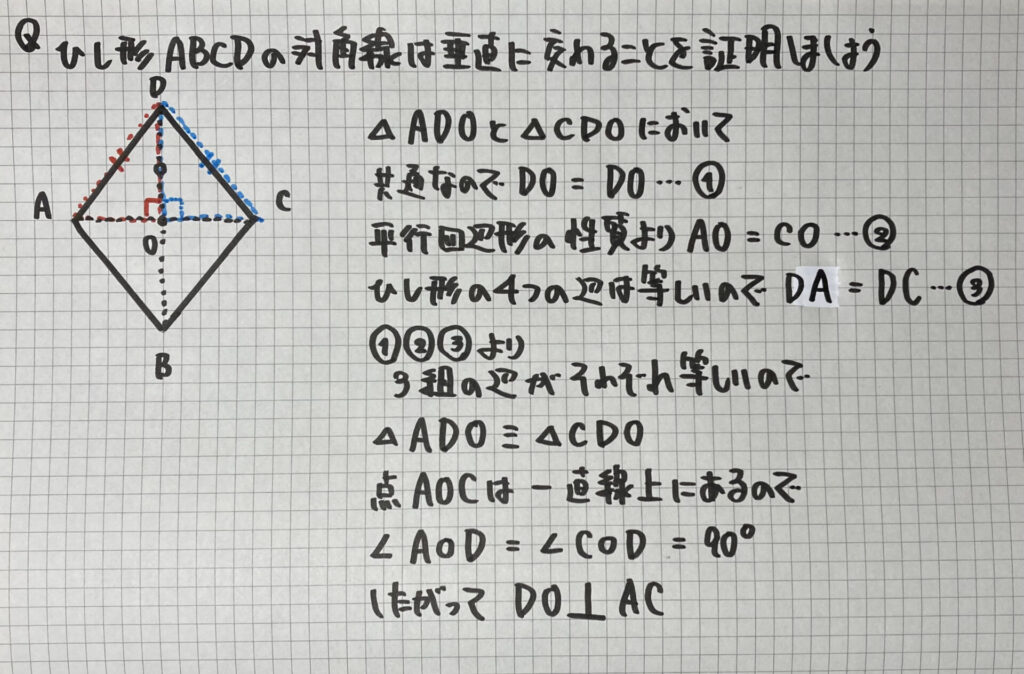
2直線が
「垂直」に交わる証明は
この問題の証明でも
あとは「流れ」を
確認しておきましょう
「折り返した図形」の証明
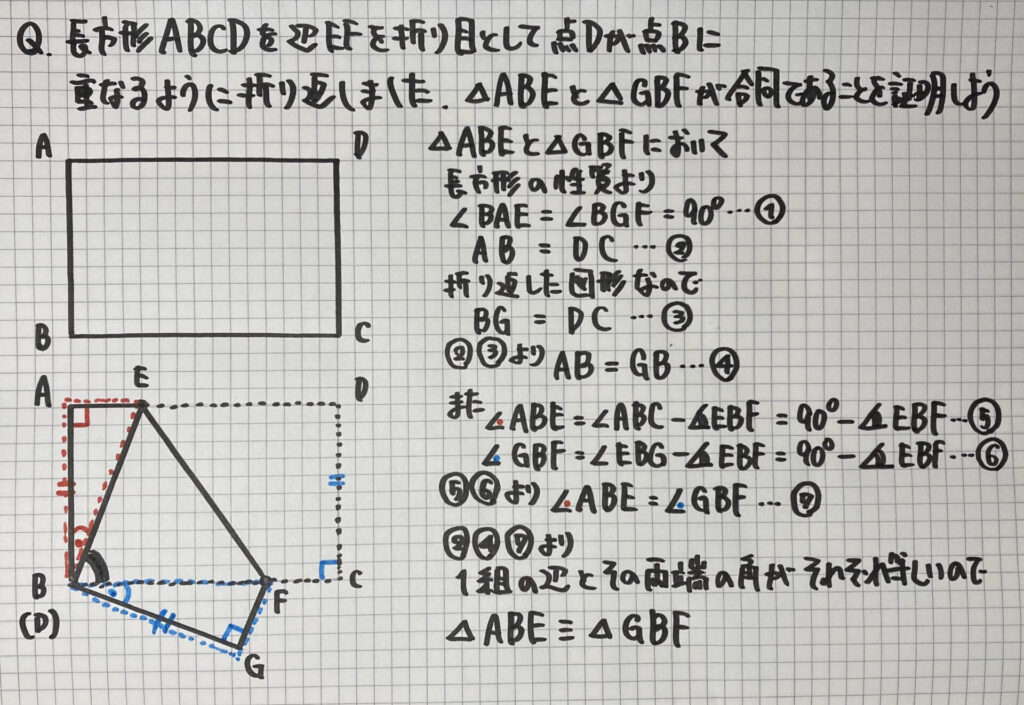
中3、そして「入試」
でもよく出る
「折り返した図形」
の問題です
折り返す「前」の
- 辺の長さ
- 角の大きさを
折り返した「後」の
図形に書き込みましょう
具体的には
証明の①にある
- $\angle BGF$「後」=$\angle DCF「前」$
証明の③にある
- BG「後」=DC「前」
の2つを
この証明では利用しています
あとは
⑤⑥の等式から
⑦の等式を作る形
はよく出てくるので
しっかり
練習しておきましょうね
いろいろな四角形のまとめ

・いろいろな四角形の性質
台形→平行四辺形→$\frac{ひし形}{長方形}$→正方形
条件が加わった後の四角形は
その前の図形の性質を持っています
・いろいろな四角形の定義
長方形
「4つの角が全て等しい四角形」
ひし形
「4つの辺が全て等しい四角形」
正方形
「4つの辺が全て等しく、4つの角が全て等しい四角形」
・四角形の対角線の性質
長方形…「長さ」が等しい
ひし形…「垂直」に交わる
正方形…「長さ」が等しく「垂直」に交わる
・折り返した図形
折り返す「前」の
- 辺の長さ
- 角の大きさを
折り返した「後」の
図形に書き込みましょう
以上、「数学嫌いな人が、
数学を楽しく好きになって欲しい」
かずのかずぶろぐでした