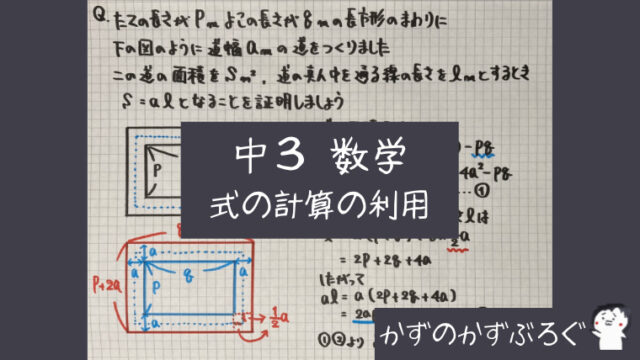
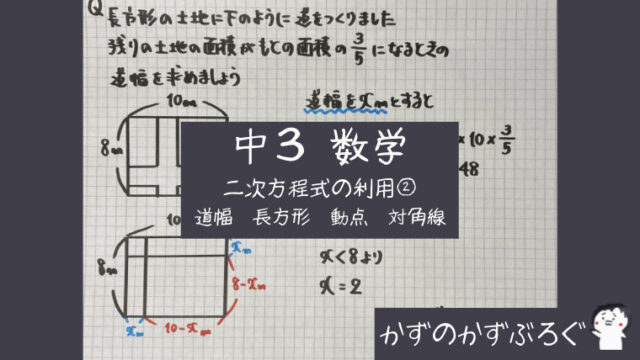
前回
展開の公式
「乗法公式」について
学習しました
こちらで
確認してくださいね

今回は
この公式を逆向きに
利用します
この計算を
「因数分解」と
いいます
中1で
「素因数分解」を
学習しましたね

名前は似ていますが
行う計算の形が違うので
注意してくださいね
では
一緒にやっていきましょう
共通因数でくくる

まず言葉の
説明からいきましょう
では
ノートの最初にも
まとめていますが
つまり
展開の時と
「逆方向」の計算
を行います
(2)ですが
「$4xy−2x$」は
「2」が共通しているので
「$4xy−2x=2(xy−x)$」
で計算を終わっては
いけません
まだ共通しているもの
「$x$」
があるので
「$4xy−2x=2(2xy−x)=2x(2y−1)$」
が正しい答えです
もし、最初に
全ての「因数」が見つからなくても
「$4xy−2x=2(2xy−x)=2x(2y−1)$」
のように
「2度」計算しても
大丈夫です
$x^2+(a +b)x +ab$型

前回、学習した
「$x^2+(a +b)x +ab=(x +a)(x +b)$」
の公式では
「$a$」「$b$」
を求めないといけません
- 積「ab」から「a」と「b」の組みを考える
- 和が「a +b」になるものを見つけます
(1)で見てみましょう
- 積「6」から「a」と「b」の組みを考える
- 和が「5」になるものを見つけます
「2」と「3」ですね
→$(x +2)(x +3)$<$(x +3)(x +2)$でもOK>
(2)からは
全ての組みを書いていません
最初慣れないうちは
「全て書き出して」
考えましょう
しばらく練習すると
頭の中で探すことが
できるようになりますよ
$a^2±2ab+b^2$型

次の公式も
乗法公式の逆ですね
- 式が「$a$の2乗」「項」「$b$の2乗」になっている時
- 真ん中の「項」が「$ab$の積の2倍」になっている時使える
(1)で見てみましょう
- 式が「$x$の2乗」「$+6x$」「$3$の2乗」になっています
- 真ん中の「$+6x$」は「$x×3$の2倍」になっているので使えます
(2)は
- 最後の項…「$16=4^2$」
- 真ん中の項…「$4×2=8$」
とすぐに見つけることができますよね
(3)は
先頭の「$9y^2$」は「$(3y)^2$」ですね
「真ん中の係数」に注意です
(4)は
最後の項に文字が入っています
「$25y^2$」に注意です
$a^2−b^2$型
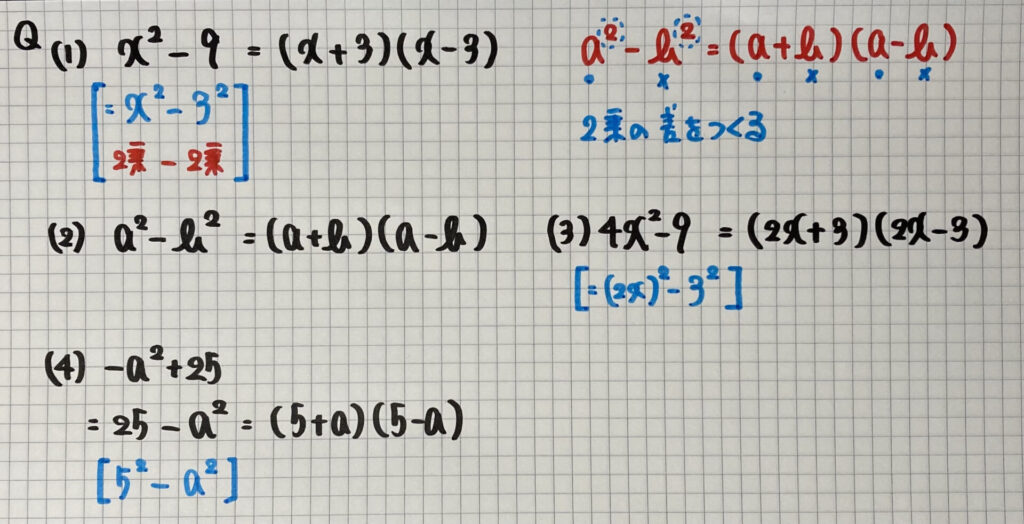
最後の公式です
これも
乗法公式と逆ですね
- 式が「$a$の2乗」−「$b$の2乗」になっている時
- 「和と差の積は2乗の差」の逆が使える
(1)で見てみましょう
- 式が「$x^2$−$3^2$」になっています
- 2乗の差=(和)×(差)が使えます
(4)は気をつけましょう
項の順番を逆にして
「2乗−2乗」の式を作ります
因数分解①公式のまとめ

・因数
「整数や式を、積の形で表した時の、個々の整数や式のこと」
例 6の因数は「1 2 3 6」
・因数分解
和の形の式を
↓計算して
積の形で表すこと
最も基本的なもの
$Ma +Mb$
↓(因数分解する)
$M(a +b)$
・共通因数で因数分解すること
「式を(共通因数で)くくる」と言う
・因数分解の公式
- $x^2+(a +b)x +ab$=$(x +a)(x +b)$
- $a^2+2ab +b^2$=$(a +b)^2$
- $a^2−2ab +b^2$=$(a −b)^2$
- $a^2 −b^2$=$(a +b)(a −b)$
乗法公式と逆になっています
以上、「数学嫌いな人が、
数学を楽しく好きになって欲しい」
かずのかずぶろぐでした