前回
「平行線と線分の比」
について
学習しました
【中3数学】「平行線と線分の比」の問題 どこよりも簡単な解き方・求め方今回は、今まで学習した「相似な図形」を利用して「平行線と線分の比」について「ピラミッド型」「砂時計型」「平行線にはさまれた線分の比」を一緒に見ていきましょう...
この考え方と
その前に学習した
「相似」を使って
図形の問題を
解くのによく利用する
- 「角の二等分線定理」
- 「中点連結定理」
を一緒に
見ていきましょう
「角の二等分線定理」の証明
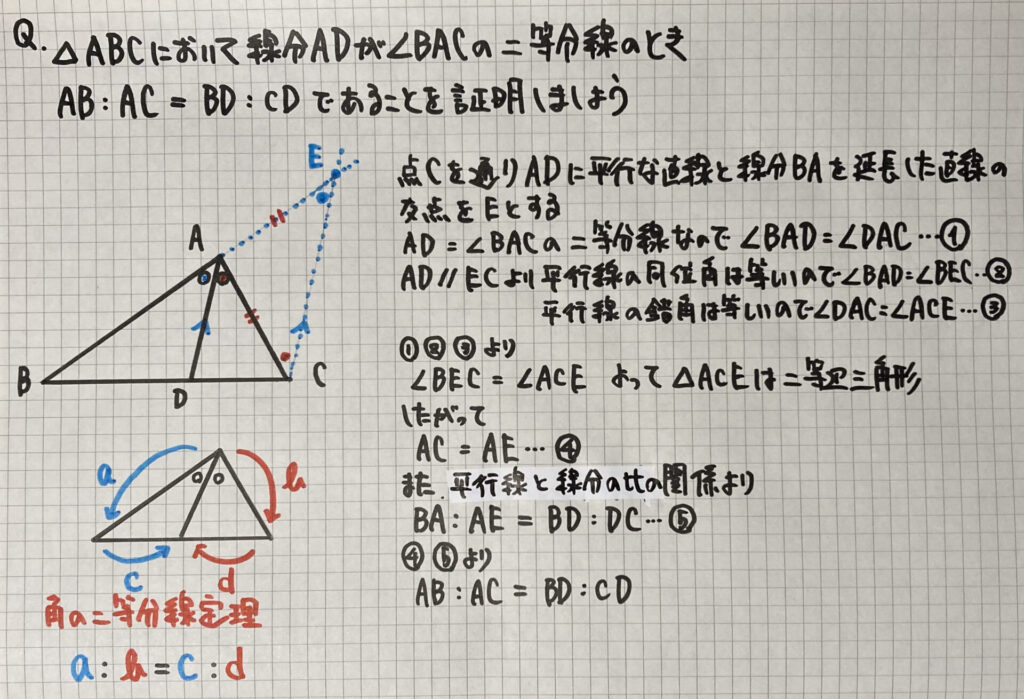
まずは
「角の二等分線定理」
の証明です
点Cから
「角の二等分線」と平行な直線を引いて
BAの延長した直線の交点をEとします
ここでできる
△ACEが
「二等辺三角形」である
ことを利用して
「平行線と線分の比」
を使って
証明することができます
練習問題
角の二等分線定理
「左：右＝左：右」で
覚えましょう
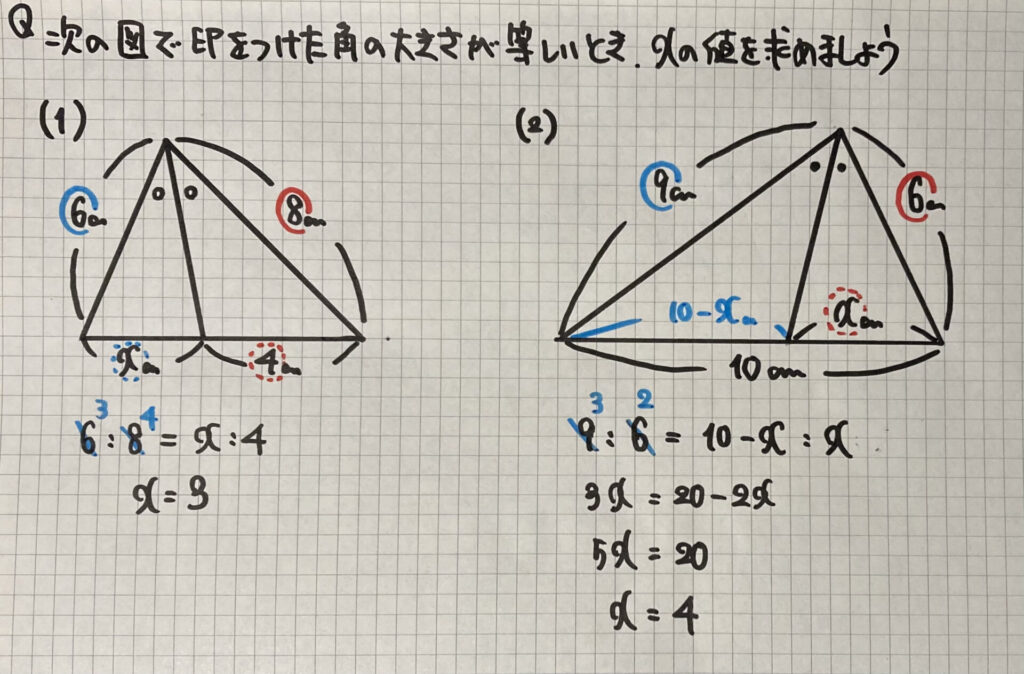
を利用して
比例式を作りましょう
「中点連結定理」の証明
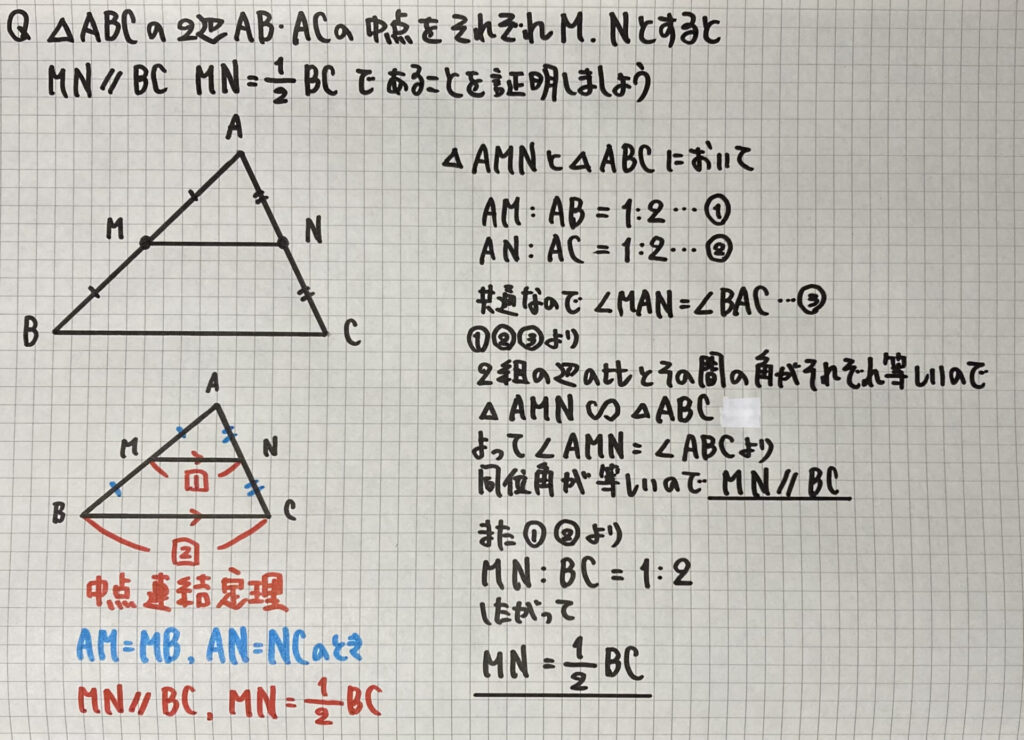
次に
「中点連結定理」
の証明です
相似の証明
↓
- 角度が等しい(平行)
- 線分の長さの比(1：2)
を証明することができます
「線分の比と平行線の関係」
からも証明することが
できますよ
中点連結定理
中点が出てきたら
↓
中点同士を結ぶと
- 平行
- 長さ(半分・2倍)
を作ることができる
練習問題(四角形)
四角形の中点を全て結ぶ
↓
「平行四辺形」
を作ることができます
対角線の長さが
等しい四角形
↓
中点連結定理を利用
↓
できた
「平行四辺形の辺」が
対角線の半分の長さ
で等しくなる
↓
「ひし形」となります
練習問題(線分)
図形の問題で
- 「中点」
- 「○等分する点」
が出てきたら
それらの点を結んで
「中点連結定理」
- 平行
- 長さ(半分・2倍)
を利用して
線分の長さを
求めることができます
角の二等分線定理・中点連結定理のまとめ
・角の二等分線定理
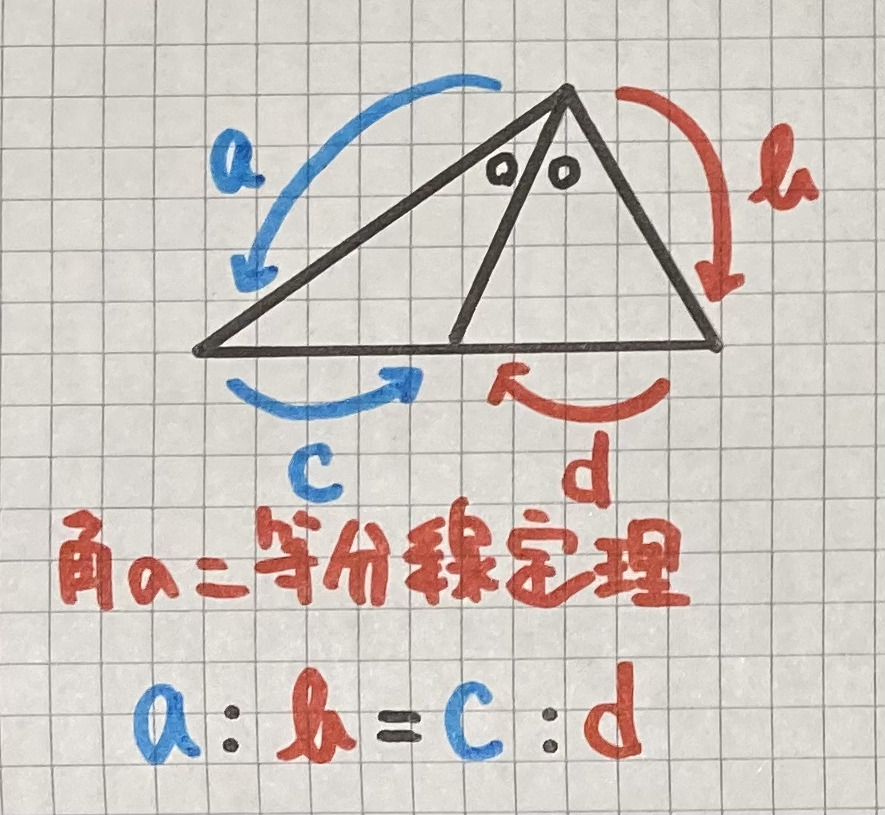
「左：右＝左：右」です
・中点連結定理
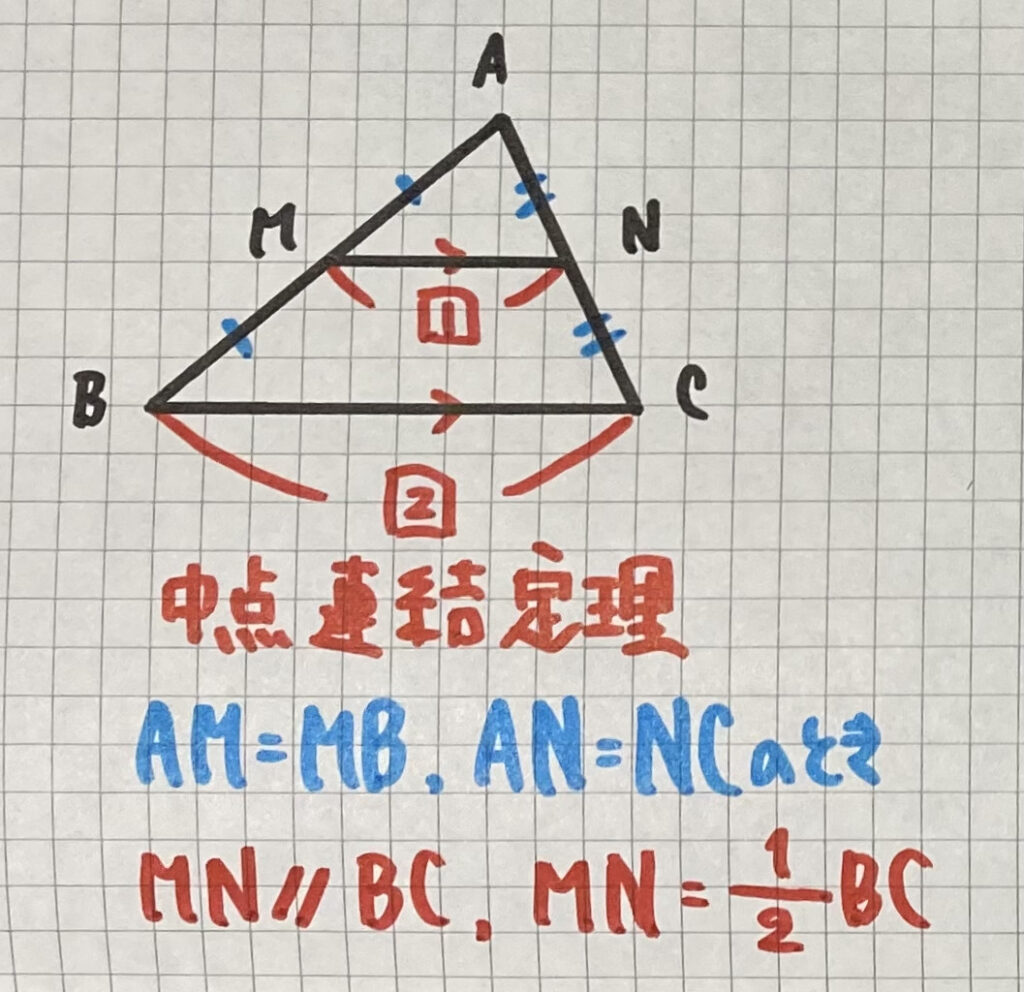
中点同士を結ぶ
- 平行
- 長さ(半分・2倍) を作る
以上、「数学嫌いな人が、
数学を楽しく好きになって欲しい」
かずのかずぶろぐでした
