前回
「$y=ax^2$」の
「グラフ」「変域」
「変化の割合」を
学習しました

今回は
「$y=ax^2$の利用」として
「制動距離」「ふりこ」
「図形の移動」
「放物線と直線」
を一緒に見て
いきましょう
「制動距離」の問題

車の「制動距離」が
「2乗に比例する関数」
になるので
よく出される問題です
解き方は
特に難しくありません
数字が「小さく」なる
ことが多いので
「ふりこ」の問題

「ふりこ」も
「周期と長さ」が
「2乗に比例する関数」
になるので出てきます
こちらは
に気をつけましょう
「図形の移動」の問題
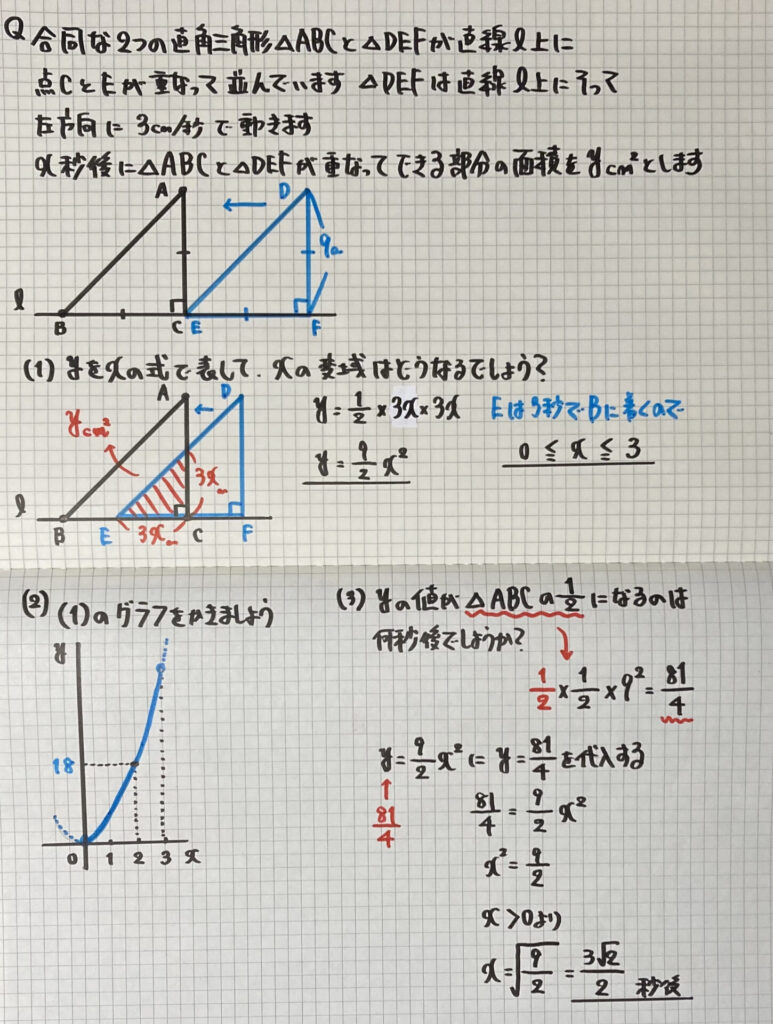
合同な図形が
移動して重なる問題です
移動した時の
「図形の様子」を
自分で書いてみる
ことが大切です
(1)は
長さを文字で表して
式を作りましょう
変域は
移動する点(E)が
点Bに着くのに
「何秒かかるか」
を考えましょう
(2)は
変域のあるグラフですね
(3)は
代入した
「二次方程式」を解きます
最後に
$x$は時間なので
$x>0$の
解の吟味を
忘れないようにしましょう
「放物線と直線」の問題

中2「$y=ax +b$」
中3「$y=ax^2$」
を合わせた
有名な問題です
問題の設定は
色々あるのですが
がよく出される問題です
(1)は
「交点」なので
↓
代入して求めましょう
(2)は
「直線を求める式」です
解き方は
- 連立方程式
- 傾き→方程式
の2通りあります
- 連立方程式は
計算に時間がかかり
ミスすることが多くなるので
- 傾き→方程式
で解くことを
おすすめします
(3)は
斜めの三角形の面積です
ノートにもあるように
左と右の2つの三角形に分けて
求めることができますが
最後にまとめたように
で求めることが
できるようになりましょう
(4)は
頂点を通る三角形の面積二等分ですが
三角形の面積二等分

これを利用して
求めます
原点を通る直線
↓
$y=ax$に代入しましょう
「放物線と直線」の公式

ここで有名で
とても便利な公式です
「$a(p +q) $…」
前回やりましたね
そうです「変化の割合」の
公式でした
中2の「一次関数」を
少し思い出してください
「変化の割合…」
「$y=ax +b$…」
「傾き…」
でしたね

これを利用して
「放物線と直線」
の公式として
この直線の式を
簡単な公式で
求めることができます
なぜ
「公式がこうなるか」
ノートで一度
確認してみてください
「代入して進める」
だけなので
是非、読んでみてくださいね
関数$y=ax^2$の利用のまとめ

・「$y=ax^2$」の利用
- 車の制動距離
- ふりこの周期と長さ
・座標上の三角形の面積
$\frac{1}{2}×幅×幅$
・三角形の面積二等分
頂点を通る二等分線
↓
通る点の対辺の「中点」を通る直線
・「放物線と直線」の公式
- $y=ax^2$に交わる
- 直線の
- 交点の$x$座標を$p、q$とする
直線の式
$y=a(p +q)x−apq$
傾き…「$a(p +q)$」
切片…「$−apq$」
以上、「数学嫌いな人が、
数学を楽しく好きになって欲しい」
かずのかずぶろぐでした