前回
「証明のしくみと進め方」
について学習しました
かずのかず
こちらで
確認してくださいね

【中2数学】「証明のしくみと進め方」の問題 どこよりも簡単な解き方・求め方今回は「証明」という単元を学習します 少し前に「式の説明」を学習しました 「説明」とは少し違う「証明」についてまず「しくみと進め方」について一緒に見ていきましょう...
今回は
「三角形の合同」
を使った証明を3問
一緒に見ていきましょう
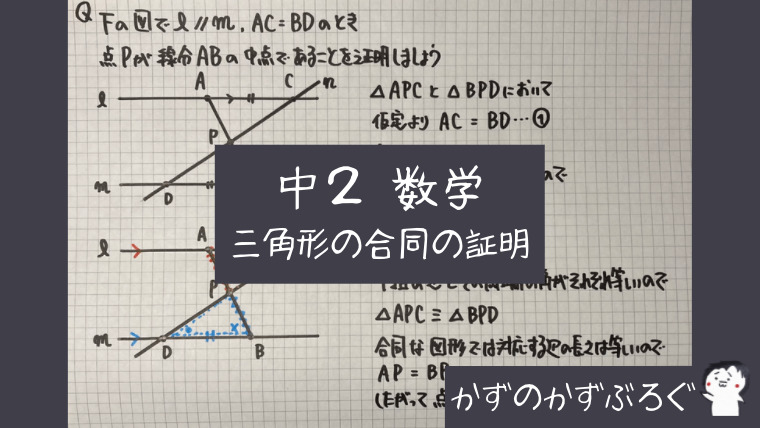
対応する辺の長さの証明①
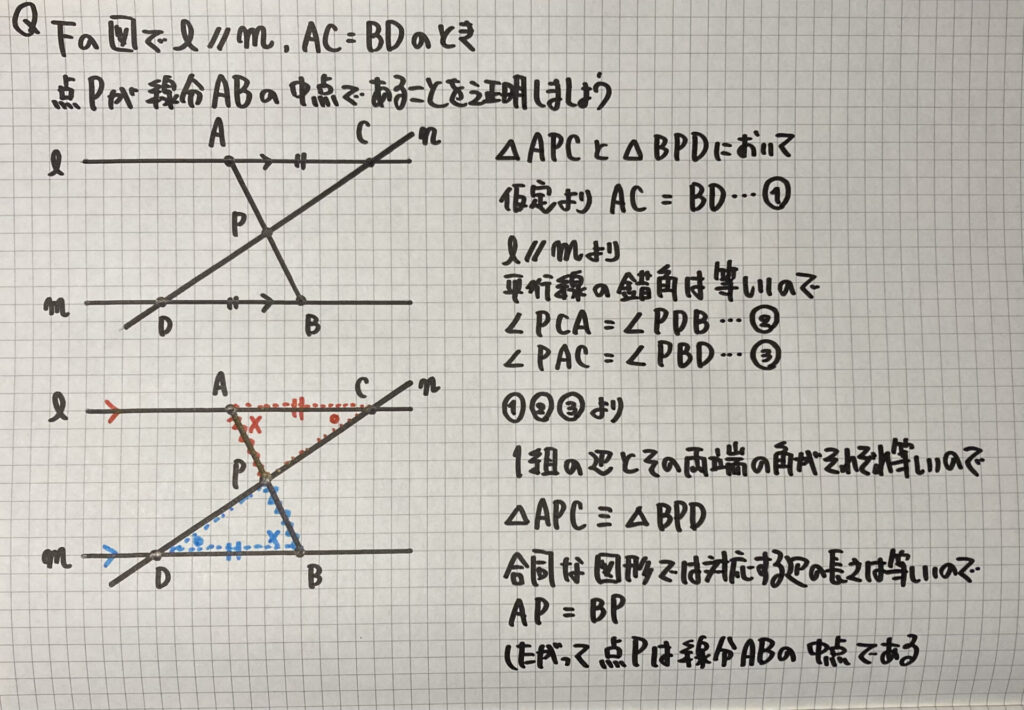
問題文には
「対応する辺の長さは等しい」
という結論はありません
この問題の「結論」は
「点Pが線分ABの中点である」ですね
この問題は
「点Pが線分ABの中点である」
ということは
「線分AP=線分BP」
を証明すれば
結論に
つなげることができる
このように考えましょう
次に実際のやり方です
ノートの下の図
(赤と青で色分け)を
見てください
対応する辺の長さが等しい証明
- 対応する辺に印を入れる
- 印を入れた辺を含む三角形を1組探す
- 仮定を図に書き入れる
- 3つの「三角形の合同条件」のどれが当てはまるか考える(①の結論は使えません)
- 三角形の合同を証明する
- 「したがって…」で結論に導く
上の流れを具体的に書くと
↓のようになります
ノートの問題
- APに赤波線、BPに青波線を入れる
- △APC(APを含)と△BPD(BPを含)
- 「ℓ//m」の印を入れる→錯角が等しいので「●」と「×」を書き入れる
- 「1組の辺とその両端の角がそれぞれ等しい」が当てはまる(AC=BDは結論なので使えません)
- △APC≡△BPD
- したがって…「点Pは線分ABの中点である」
対応する辺の長さの証明②
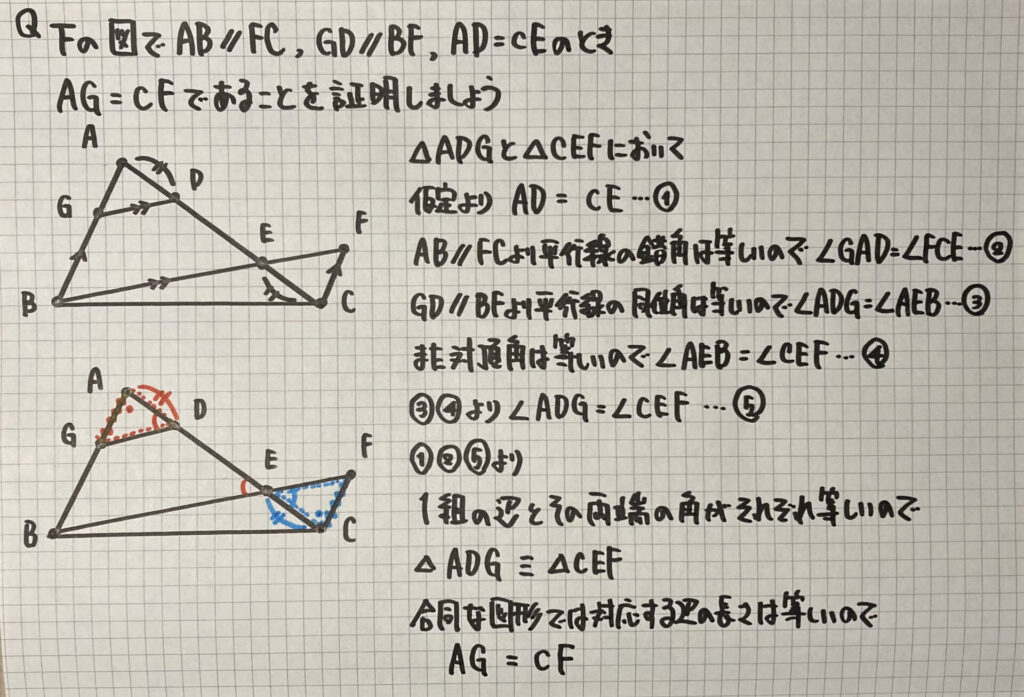
今回の結論は
問題文の通り
AG=CF
「辺の長さが等しい」
を証明します
ノートの問題
- AGに赤波線、CFに青波線を入れる
- △ADG(AGを含)と△CEF(CFを含)
- 仮定より「AD=CE」
- AB//FCより錯角は等しいので「$\angle GAD$=$\angle FCE$」
- GD//BFより同位角は等しいので「$\angle ADG$=$\angle AEB$」…③
- 対頂角は等しいので「$\angle AEB$=$\angle CEF$」…④
- ③④より「$\angle ADG$=$\angle CEF$」…⑤
- 「1組の辺とその両端の角がそれぞれ等しい」が当てはまる(AG=CFは結論なので使えません)
- △ADG≡△CEF
- 合同な図形では…「AG=CF」
少し長くなりましたが
ポイントは
③④から⑤の式を作ることです
対応する角の大きさの証明
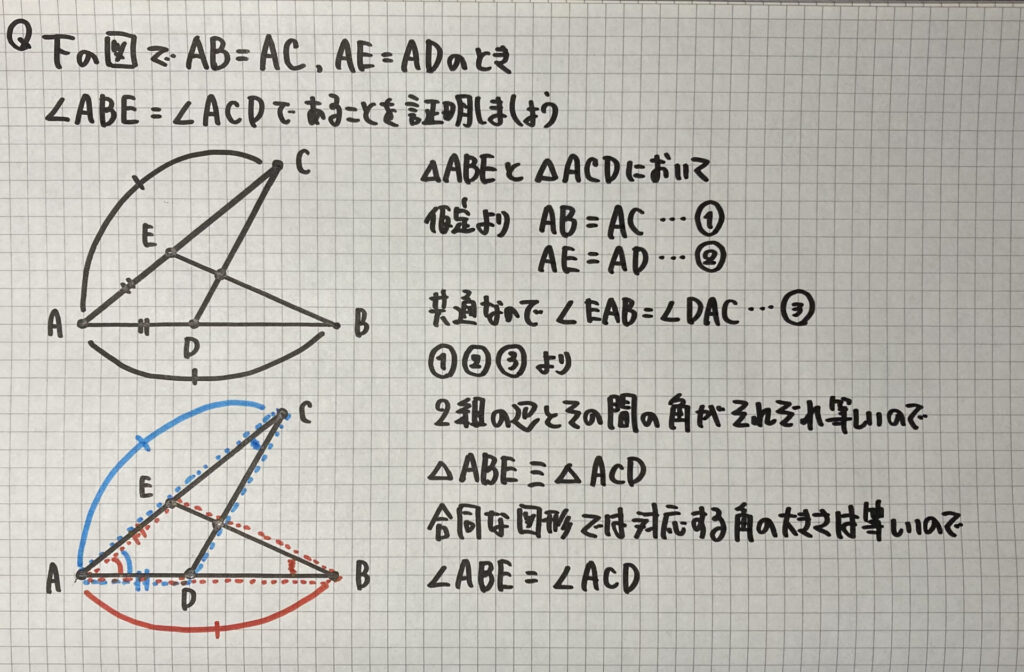
今回の結論は
$\angle ABE$=$\angle ACD$
「(対応する)角の大きさが等しい」
を証明します
「(対応する)角」は
「(対応する)辺」と
同じ流れで大丈夫です
ノートの問題
- $\angle ABE$にに赤線、$\angle ACD$に青線を入れる
- △ABE($\angle ABE$を含)と△ACD($\angle ACD$を含)
- 仮定より①②、共通な角なので③
- 「2組の辺とその間の角がそれぞれ等しい」が当てはまる($\angle ABE$=$\angle ACD$は結論なので使えません)
- △ABE≡△ACD
- 合同な図形で…「$\angle ABE$=$\angle ACD$」
三角形の合同の証明まとめ

・点Pが線分ABの中点である証明
線分AP=線分BP
を証明する
・対応する辺(角)が等しい証明
- 対応する辺(角)に印を入れる
- 印を入れた辺を含む三角形を1組探す
- 仮定を図に書き入れる
- 3つの「三角形の合同条件」のどれが当てはまるか考える(①の結論は使えません)
- 三角形の合同を証明する
- 「したがって…」で結論に導く
・証明でよく使う等式
- A=B
- B=Cより
- 「A=C」
かずのかず
以上、「数学嫌いな人が、
数学を楽しく好きになって欲しい」
かずのかずぶろぐでした