今回は
「単項式」を
「かけたり・わったり」して
計算をしていく問題です
基本のやり方は
中1で学習した
内容と同じです
こちらで
確認してくださいね

では一緒に
やっていきましょう
単項式の乗法(累乗)
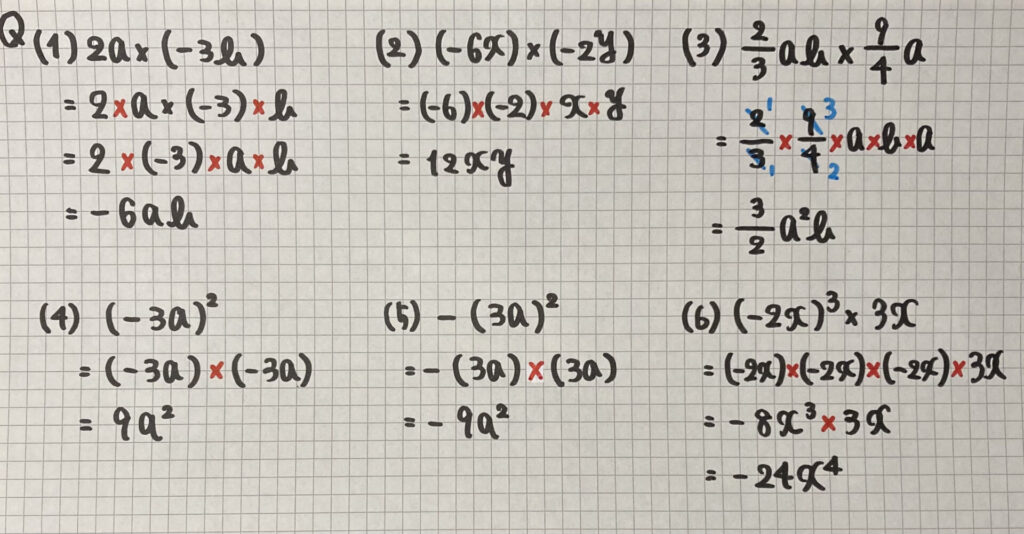
かけ算は順番を変えても
1×2×3=1×3×2
同じ答えになりました
「単項式」に「単項式」を
かけるとき
「係数の積」と
(数だけでかけ算をする)
「文字の積」を
(文字だけでかけ算をする)
計算しましょう
慣れてきたら
途中の部分を省略
(頭の中で計算)しても
大丈夫です
(4)と(5)を
見てください
間違えやすい問題です

(4)は
$(-3a)^2$
$=(-3a)×(-3a)$なので
$9a^2$ (答えは+)
(5)は
$-(3a)^2$
$=-(3a)×(3a)$なので
$-9a^2$ (答えは−)
単項式の除法

「単項式の除法」は
「分数」の形にして
計算します
(4)と(5)は
分数のわり算ですが
もちろん
「分母と分子を入れ替えてかけ算」
ですね
その前に
これで
「文字の書き間違え」が
少なくなります
あとは
繰り返しになりますが
3つの単項式の乗除
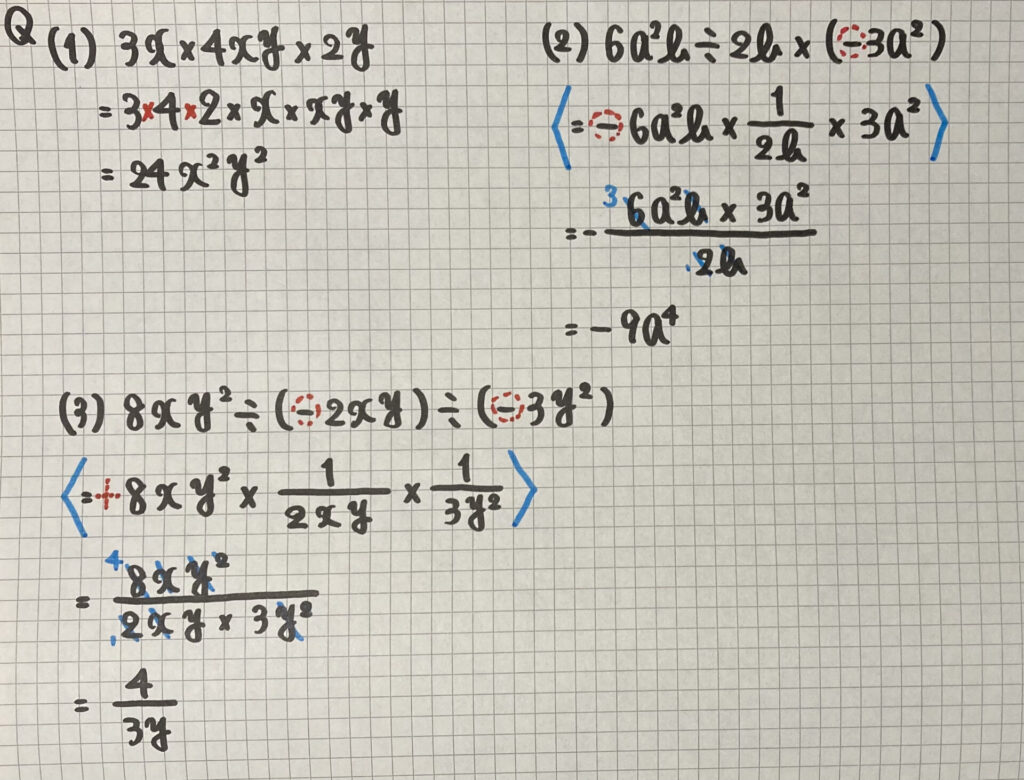
3つの単項式の
「かけ算」「わり算」が
混ざった式です
- 符号を決める(「−」の数を数える)
- わり算があれば「分数」の形にする
- $\frac{×の後}{÷の後}$で約分をする
ちなみに
式の時と分数の形にした時の
「÷」と「×」が違うので
間違えやすいですね
式の値

前回、そして
中1でもやった
「式の値」です
「単項式」の計算をしてから
「代入」して
「式の値」を出しましょう
単項式の乗法・除法のまとめ

・単項式×単項式
「係数の積」と
(数だけでかけ算をする)
「文字の積」を
(文字だけでかけ算をする)
計算しましょう
・単項式÷単項式
$単項式÷単項式=\frac{単項式}{単項式}$
「分数」の形にして
計算しましょう
・分数の単項式のわり算
$−\frac{3}{4}a$は
$−\frac{3a}{4}$と
「文字は分子に乗せる形」に
書きかえてから
計算しましょう
・3つ(以上)の単項式の乗除
- 符号を決める(「−」の数を数える)
- わり算があれば「分数」の形にする
- $\frac{×の後}{÷の後}$で約分をする
・A÷B×CとA÷B÷C
- $A÷B×C=\frac{A×C}{B}$
- $A÷B÷C=\frac{A}{B×C}$
「÷の後」が「分母」です
以上、「数学嫌いな人が、
数学を楽しく好きになって欲しい」
かずのかずぶろぐでした