今回は
「証明」という
単元を学習します
少し前に
「式の説明」を
学習しました
かずのかず
こちらで
確認してくださいね

【中2数学】「式の説明と等式変形」の問題 どこよりも簡単な解き方・求め方前回まで学習してきた「単項式・多項式の計算」を使って「式の説明」と「等式変形」を学習していきます...
「説明」とは少し違う
「証明」について
まず
「しくみと進め方」
について
一緒に見ていきましょう
証明
仮定と結論
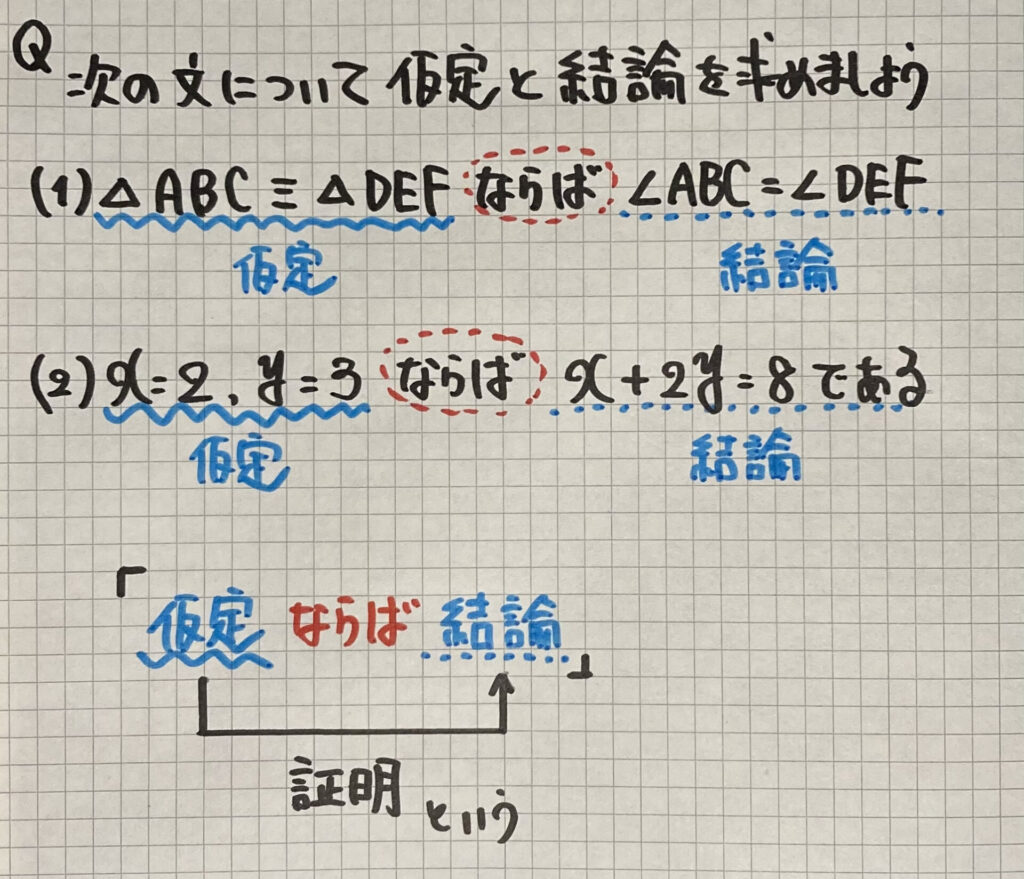
数学では
問題を考えていく際に
「○○ならば△△」
の形で表されるものがあります
この
- 〇〇の部分を「仮定」
- △△の部分を「結論」
と言います
証明のしくみ
証明のしくみ
- 仮定から始める
- すでに正しいと認められていることを「根拠」にまとめる
- 結論を導く
証明で使われる「根拠」
問題でよく使われる
「根拠」をまとめます
- 対頂角の性質
- 平行線の性質
- 平行線になるための条件
- 三角形の内角・外角の性質
- 多角形の内角・外角の和
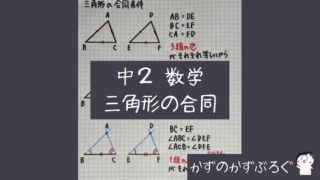
- 合同な図形の性質
- 三角形の合同条件
- 等式の性質
などです
内容を忘れてるもの
があれば復習して
おきましょうね
証明の進め方
証明の進め方
- 結論を導くための内容を考える
- 仮定や仮定から導かれる内容を整理する
- 結論に結びつける
このまま覚える
必要はありません
実際の問題で
「進め方」は
確認するので安心してください
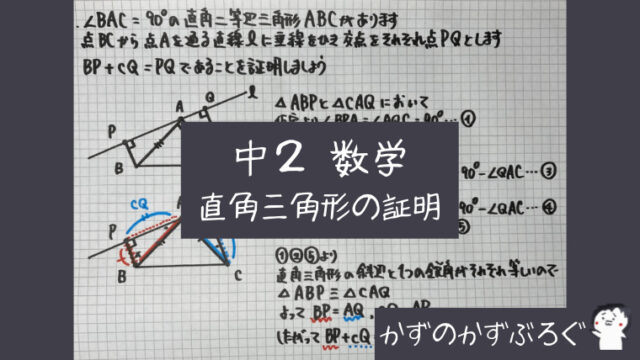
練習問題①
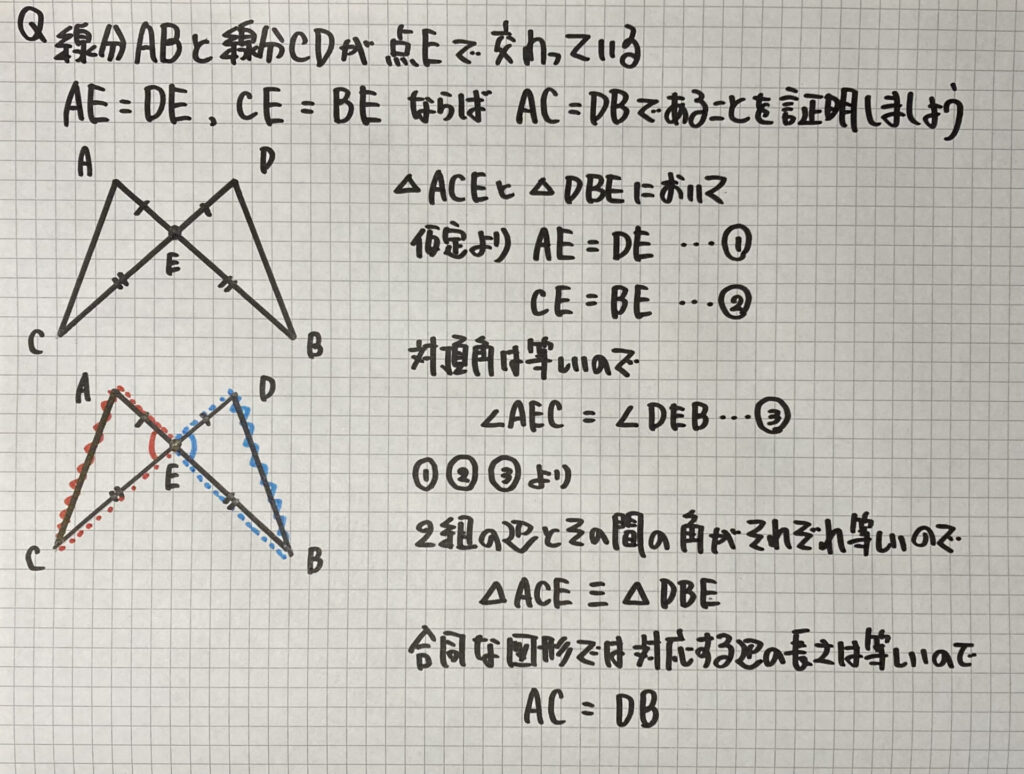
「辺の長さが等しいこと」を
証明する問題です
ここでよく使われるのが
「三角形の合同」です
このような流れで
まとめていきます
具体的には下の形です
「三角形の合同を使った」証明
- △…と△…において
- (根拠)○○=●●…①
- (根拠)△△=▲▲…②
- (根拠)□□=■■…③
- ①②③より「合同条件」
- △… ≡ △…
- 「合同な図形では対応する…は等しいので」
- 【結論】◇◇=◆◆
少し形が違う時も
あります
「細かな書き方」は
実際に問題を見て
一緒にやっていきましょう
練習問題②
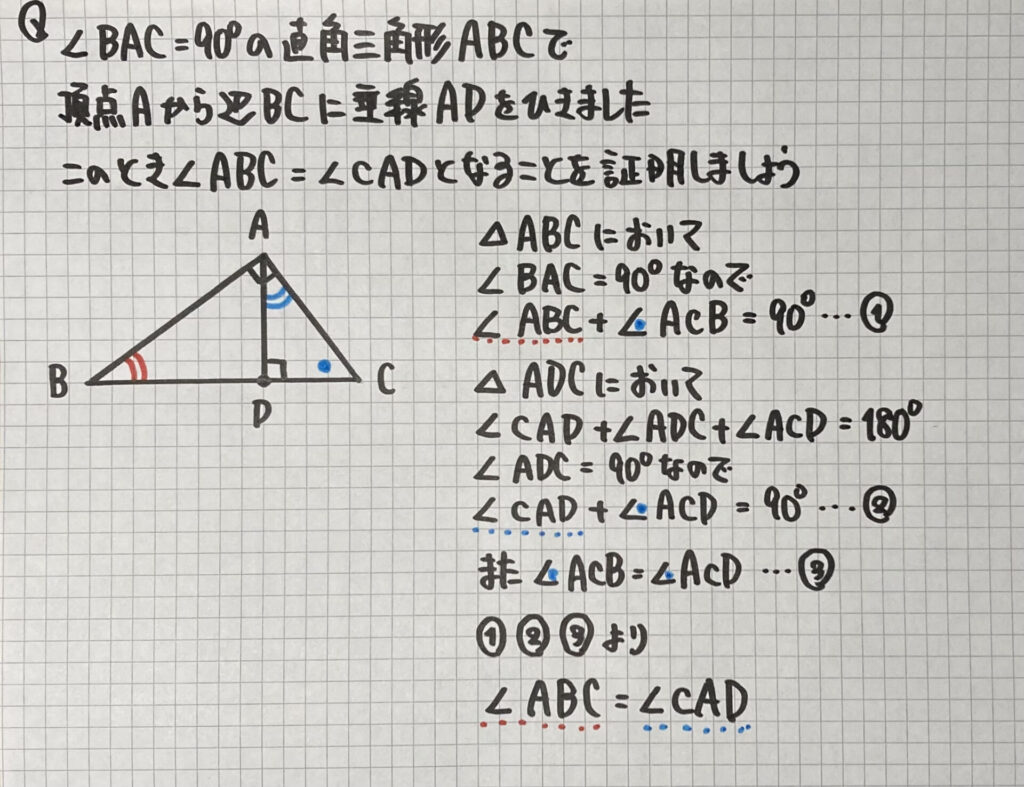
今回は
- 三角形の内角の性質
- 等式の性質
を「根拠」にして
証明していきましょう
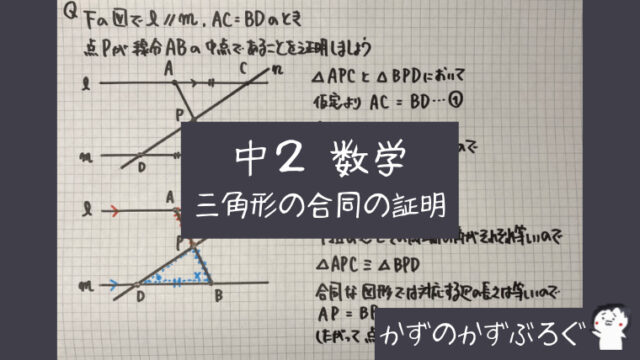
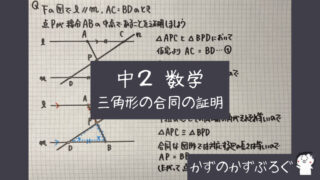
練習問題③
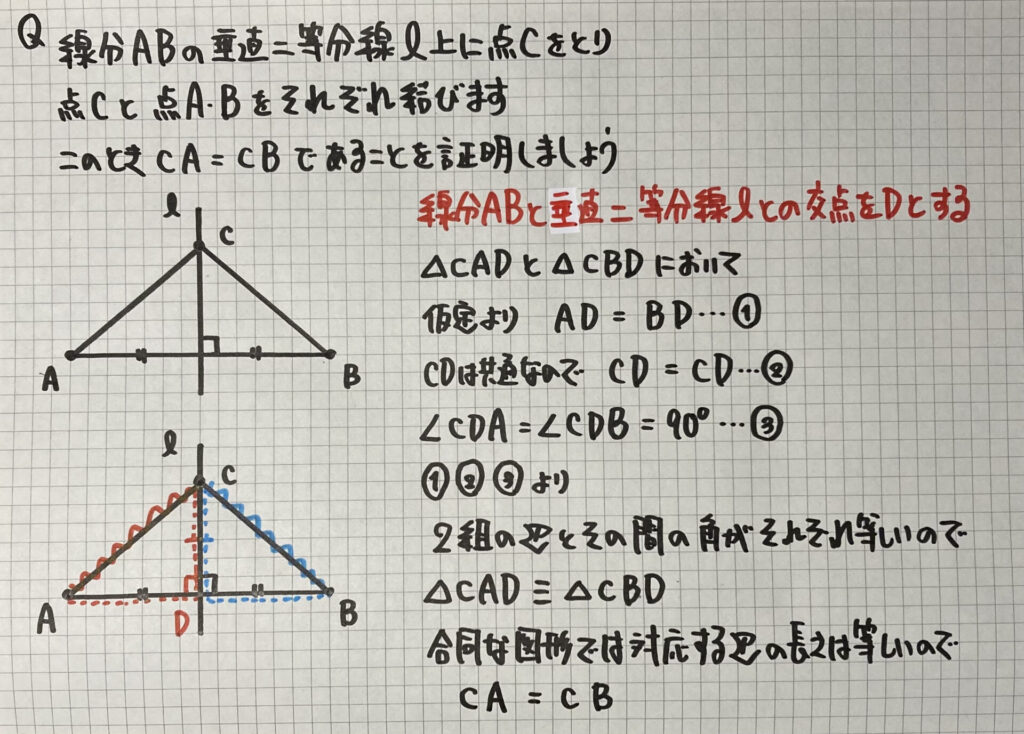
今回は
「三角形の合同を使う」証明です
ノートの最初
「線分ABと垂直二等分線ℓとの交点をDとする」
の部分です
あとは
練習問題①と
同じ流れで
証明しましょう
証明のしくみと進め方のまとめ

・どのような図形でも
「表面積の比」は
「相似比」の「2乗」になり
「体積の比」は
「相似比」の「3乗」になる
・三角錐台の図形
線分を延長して「三角推」を作る
かずのかず
以上、「数学嫌いな人が、
数学を楽しく好きになって欲しい」
かずのかずぶろぐでした