ここでは「反比例」について
やっていきます
言葉を見ると
「比例」の「反対」だから「反」比例…
なんですが、そのまま「反対」という
感じではありません
例えば
「面積が100㎠の長方形」が
あるとします
「たてが長くて横が短いもの」
「たてが短くて横が長いもの」
「たてと横がほとんど同じ長さのもの」
どれも、「長方形の面積=100㎠」ですよね
でも、「たて」と「横」の長さは
いろいろです
この時の「たて」と「横」の
「2つの数の関係」が「反比例」になります
文章だけでは「うーん…」となりますよね

実際に問題をいっしょに見ていきましょう
反比例のグラフ
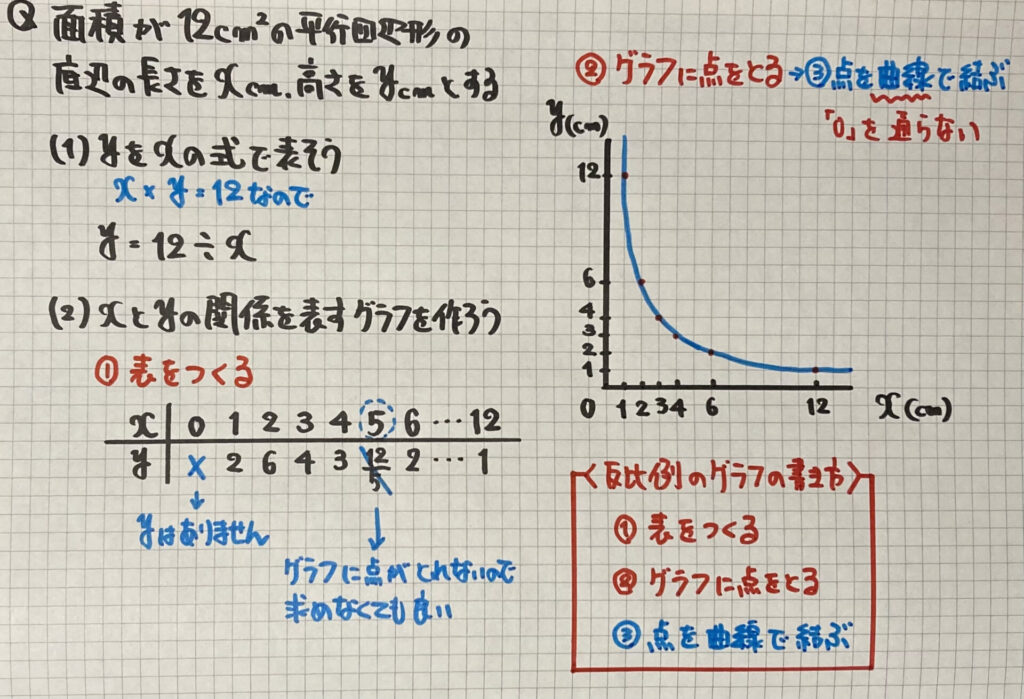
「グラフの作り方」は
$「y=(整数)÷x」$を作ります
この式から$「x」$と$「y」$を求める
ことができるようになったので
反比例の利用

文章と表から
この問題の
「速さ」を「時速$x$km」
「時間」を「$y$時間」とすると
「$xとy$が反比例の関係」に
なることがわかりますね
次に
整数を$x×y$で求めて
$「y=(整数)÷x」$を作ります
そして$「x」$や$「y」$に
「数」を入れて<代入(だいにゅう)といいます>
求めましょう
反比例のまとめ

・反比例とは
ともなって変わる2つの数(量)で
一方が2倍 3倍…になると、
もう一方は$\frac{1}{2}$倍 $\frac{1}{3}$倍…になる関係
・反比例の式
$y=整数÷x$
反比例のグラフ
点を「曲線」で結ぶ
(グラフは「0」を通りません)
かずのかず
以上、「算数嫌いな人が、
算数を楽しく好きになって欲しい」
かずのかずぶろぐでした