【小6算数】「比例とグラフ」の問題　どこよりも簡単な解き方・求め方

算数では、いっしょに変わっていく2つの数（量）がよく出てきます

ここでは「比例」という関係について見ていきましょう

小学5年生の時にも勉強しましたね

【小5算数】「比例」の問題　どこよりも簡単な解き方・求め方比例とはともなって変わる2つの数（量）で一方が2倍 3倍…になるともう一方も2倍 3倍…になる関係のことです　比例の式　○＝ある数×□ （○と□の場所に注意しましょう！）...

こちらで確認してくださいね

今回は、この「比例」の

「グラフ」や「利用（文章題）」

について見ていきましょう

比例の性質

まず、「比例の性質」について

もう一度確認していきましょう

でしたね

$「x」$の変わり方が「$\frac{4}{3}$」倍になると

$「y」$の変わり方も「$\frac{4}{3}$」倍に

比例なので「同じ」になりますね

比例の式

⑴$「yはxに比例しているか」$は

$xとy$の表を「横に」見ていきましょう

$「xとyの値がどちらも、2倍　3倍…になっている」$ので

「比例している」と言えますね

⑵$「yをxの式で表す」$とは

$「y＝（整数）×x」$を作ることです

$xとy$の表を「たてに」見ていきましょう

$「どこを見てもyはxの3倍になっている」$ので

$「y＝3×x」$となります

比例のグラフ

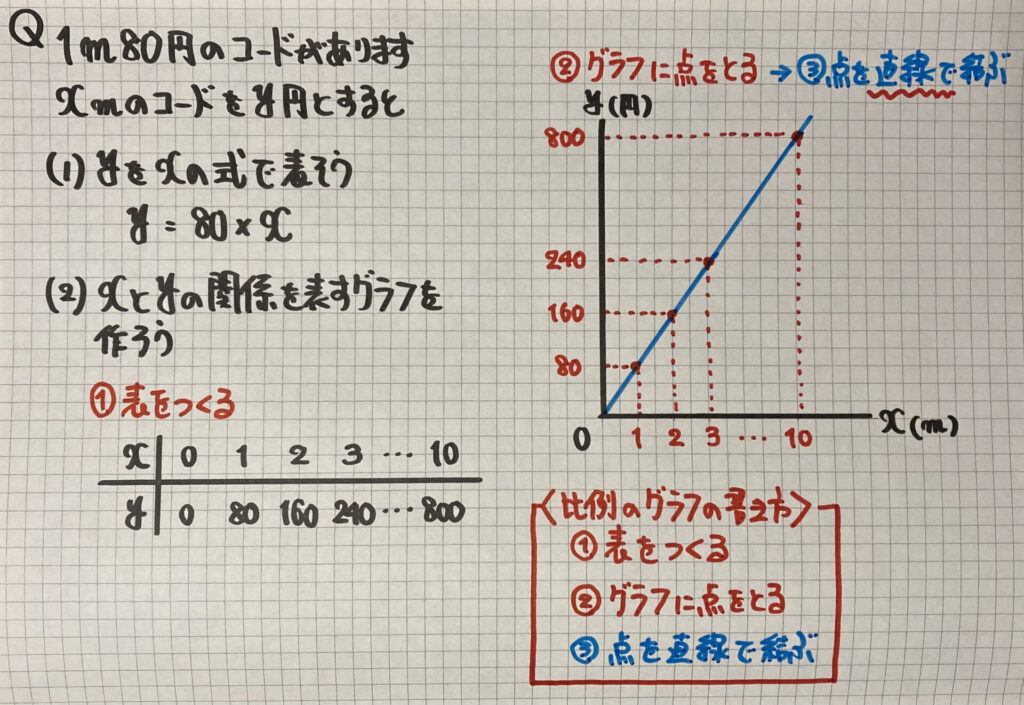
「グラフの書き方」は

$「y＝（整数）×x」$を作ります

この式から$「x」$と$「y」$を求める

ことができるようになったので

比例の利用

速さとグラフ

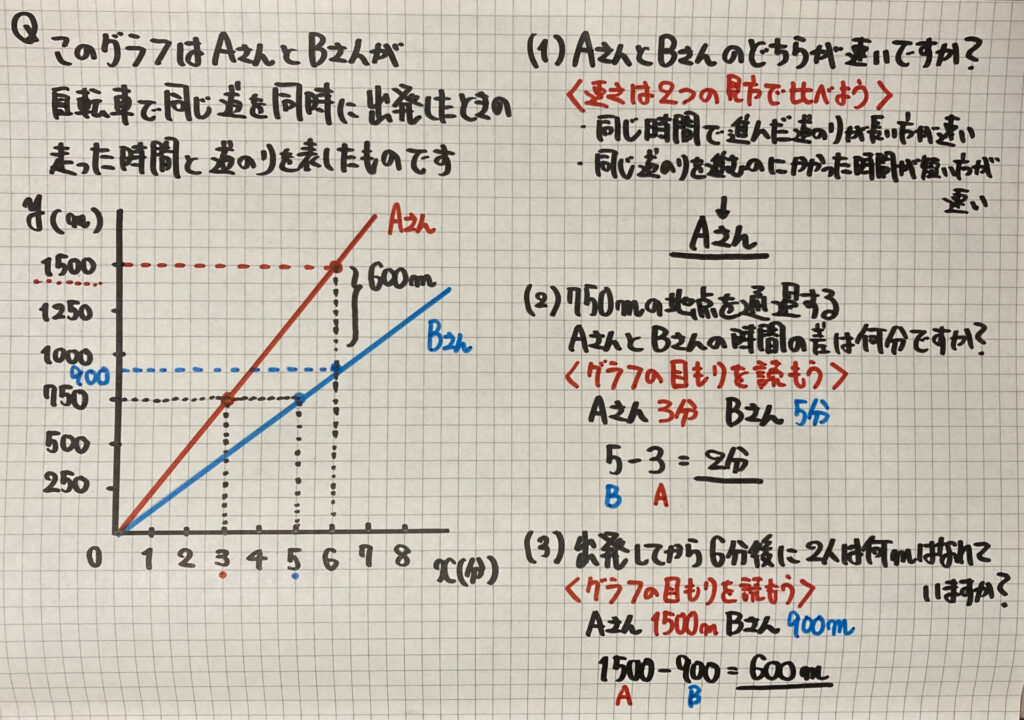
「速さ」を「比例のグラフ」で

表すことができます

⑴「速さ」はノートにあるように

2つの比べ方があります

また、グラフの特ちょうとして

⑵⑶は「速さ」の問題として

「計算」で求めることもできますが

「グラフを読み取る」ことで

簡単に求めることができますよ

文章題と比例式

比例の文章題は

そして$「x」$や$「y」$に

「数」を入れて＜代入（だいにゅう）といいます＞

求めましょう

また、別の求め方として

「比の式＜比例式（ひれいしき）といいます＞」

で求めることもできます

【小6算数】「比」の問題　どこよりも簡単な解き方・求め方「比」とは「割合」を表す1つの方法です　比の値とは、○：△→○÷△　内項の積＝外項の積とは、○：△＝□：▼のとき　△×□＝○×▼...

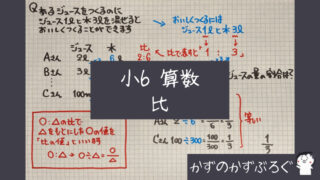
こちらで確認してくださいね

比例とグラフのまとめ