今回は
「図形」の「基本の作図」です
作図では
ルールがあって
使えるのは
- 定規
- コンパス
だけです
- 三角定規
- 分度器
は使えません
学校のテストには
出ることが多いですが
入試に関しては
学校によって様々です
「作図」は
「図形の特ちょう」を
理解するにも役に立つので
一緒にしっかり見ていきましょう
「垂直二等分線」の作図
まずは言葉の説明です
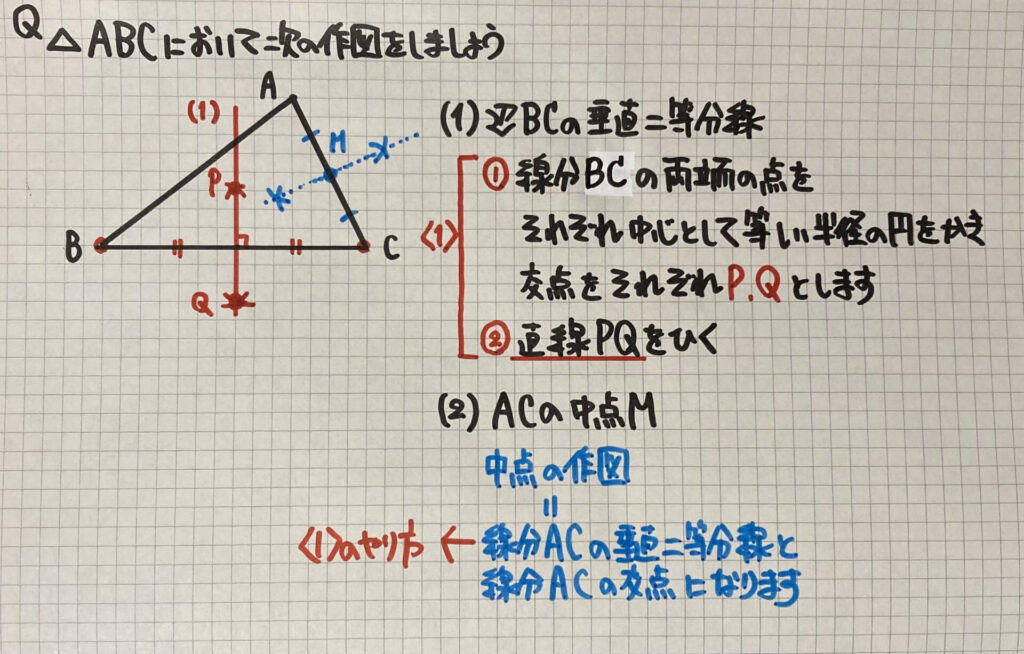
⑴ですが
△ABCの辺(線分)BCに
注目しましょう
ノートに書き方はありますが
大切なので
ここでもまとめますね
- 線分BCの両端の点をそれぞれ中心として「等しい半径」の円をかき、交点をそれぞれPQとします
- 直線PQをひきましょう
⑵は辺(線分)ACの中点ですが
辺ACの「垂直二等分線」と
線分ACの交点が
「中点」となります
「垂直二等分線の作図」は
⑴の<1>の部分と
同じなので
確認してくださいね
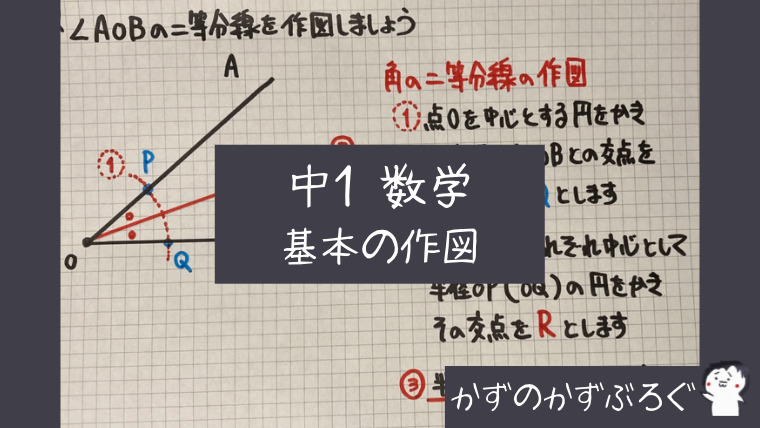
「角の二等分線」の作図
そのままの意味ですが
ここでもまとめますね
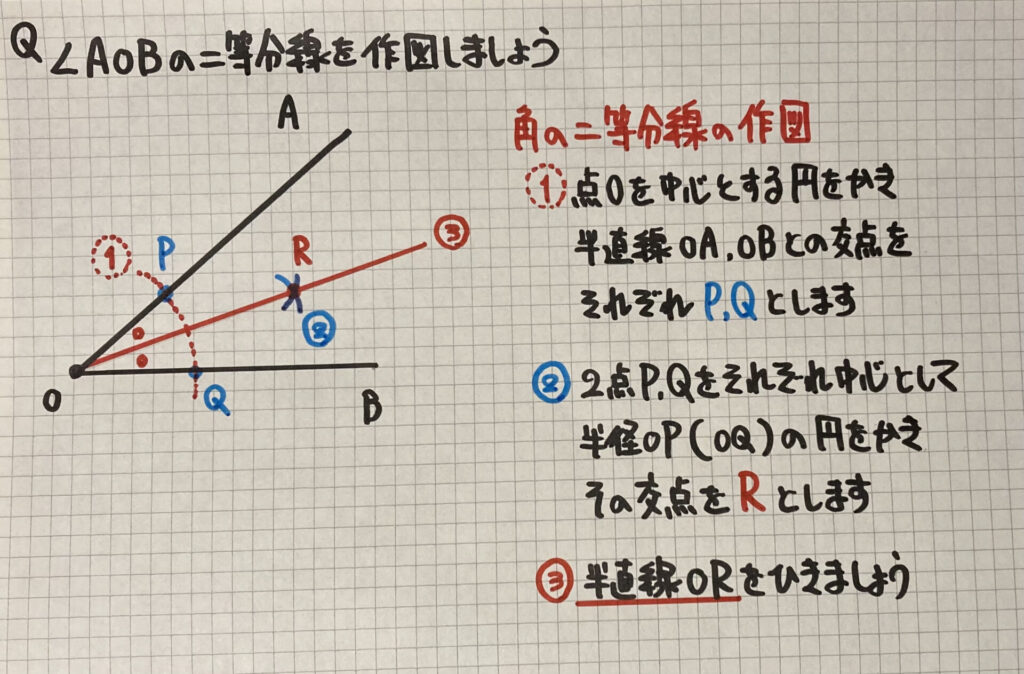
- 点Oを中心とする円をかき、半直線OA、OBとの交点を、それぞれP、Qとします
- 2点PQをそれぞれ(円の)中心として半径OP(OQ)の円をかき、その交点をRとします
- 半直線ORをひきましょう
「垂線」の作図
「垂線」…垂直な関係にある直線のことでしたね
実は
「作図」で出てくる
「垂線」は2種類あります
- 直線上の1点を通る垂線
- 直線上にない1点を通る垂線
また、先ほど学習した
「垂直二等分線」と
最初は勘違いしやすいので
気をつけてください
「垂線①」の作図
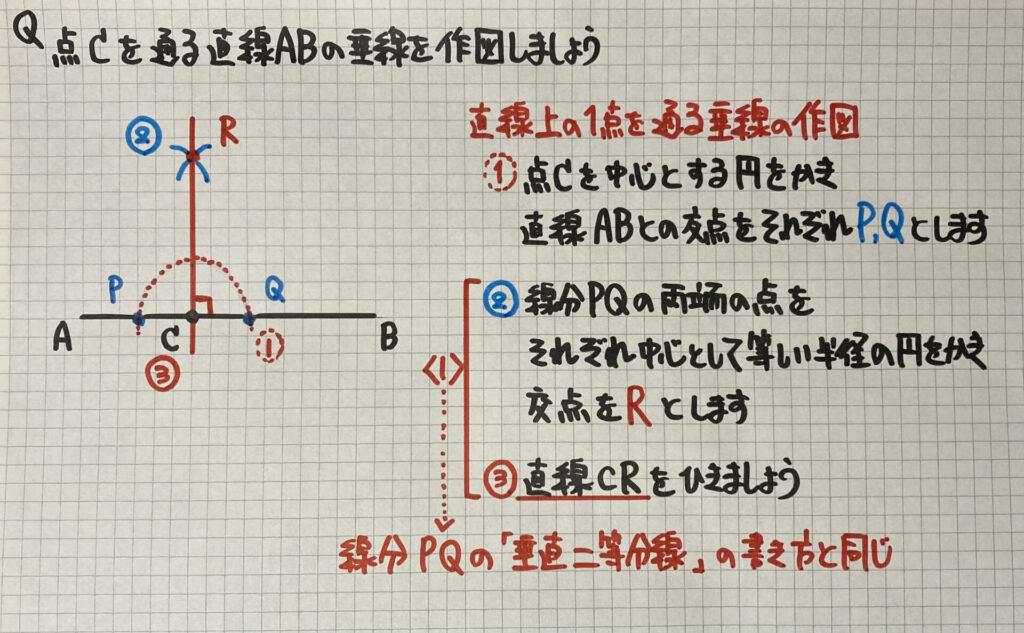
まずは
「直線上の1点を通る垂線」です
ここでもまとめますね
- 点C(直線上にある)を中心とする円をかき、直線ABとの交点をそれぞれP、Qとします
- 線分PQの両端の点を、それぞれ中心にして等しい半径の円をかき、交点をRとします
- 直線CRをひきましょう
よく見てみると
②③は
「垂直二等分線の書き方」と
同じになっていますね
「図形のしくみ」が分かれば
すべて「丸暗記」をする
必要はないので
安心してくださいね
「垂線②」の作図
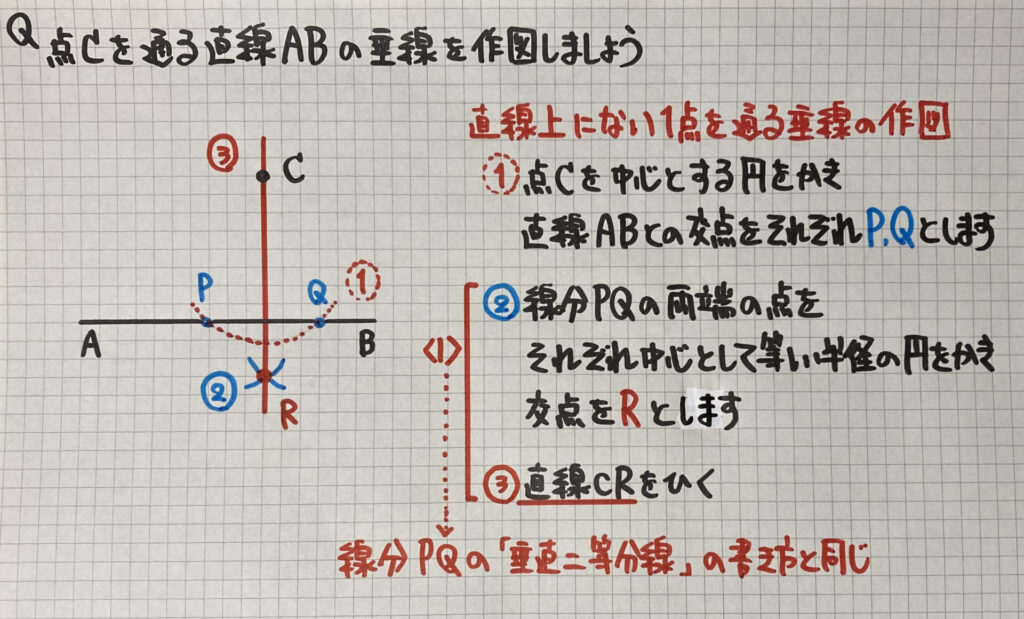
次に
「直線上にない1点を通る垂線」です
ここでもまとめますね
- 点C(直線上にない)を中心とする円をかき、直線ABとの交点をそれぞれP、Qとします
- 線分PQの両端の点を、それぞれ中心にして等しい半径の円をかき、交点をRとします
- 直線CRをひきましょう
ほとんど
「作図の方法」は同じですね
何度か練習すれば
すぐにできるようになりますよ
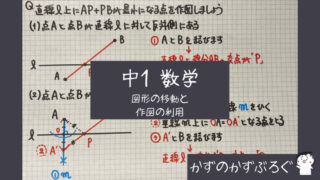
練習問題
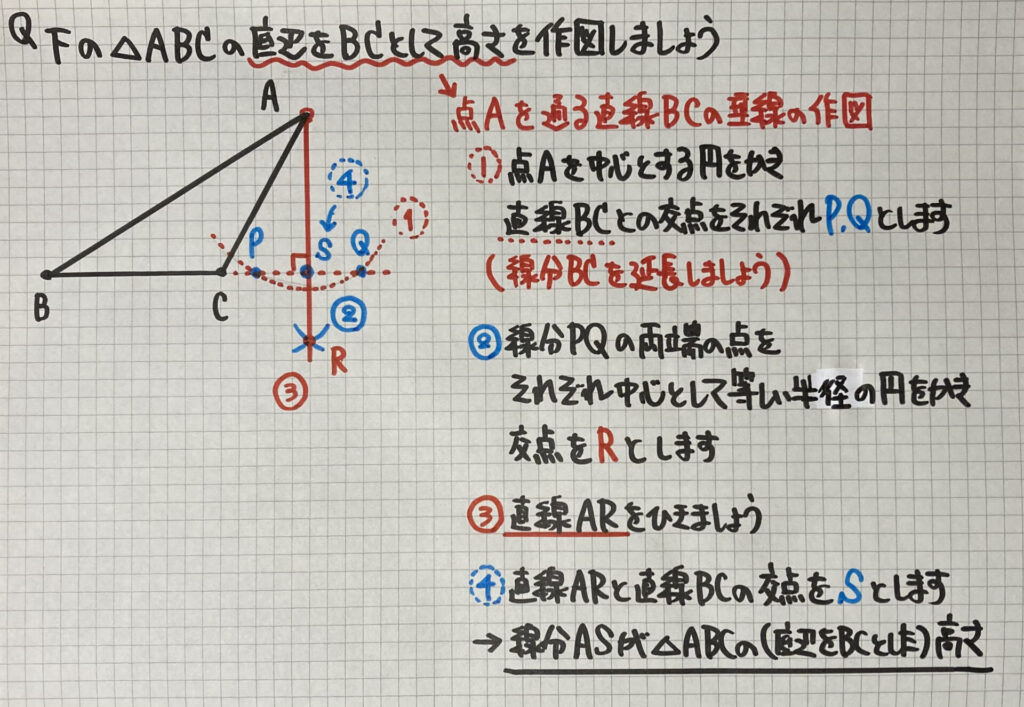
では「垂線の作図」の問題です
「底辺をBC」とするので
この三角形の高さは
「点A」から
「直線BC」へ「垂線」をひく
ことが分かりますね
この問題の大切なところは
「線分BCを直線BC」に
することです
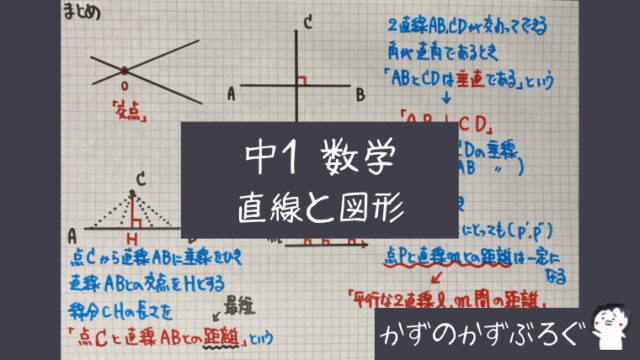
基本の作図のまとめ

・中点
線分の両端からの距離が
等しい線分上の点のこと
・垂直二等分線
線分の中点を通り
その線分と垂直に交わる直線のこと
・角の二等分線
角を二等分する半直線のこと
・2種類の垂線の作図
- 直線上の1点を通る垂線
- 直線上にない1点を通る垂線
・「垂直二等分線」と
「垂線」の違いを理解しましょう
以上、「数学嫌いな人が、
数学を楽しく好きになって欲しい」
かずのかずぶろぐでした