前回
「いろいろな四角形」
について学習しました
こちらで
確認してくださいね
今回は
三角形の
「面積を変えずに形を変える」
(等積変形)
について
四角形を利用して
学習します
では、一緒にやって
いきましょう
平行線と三角形の面積
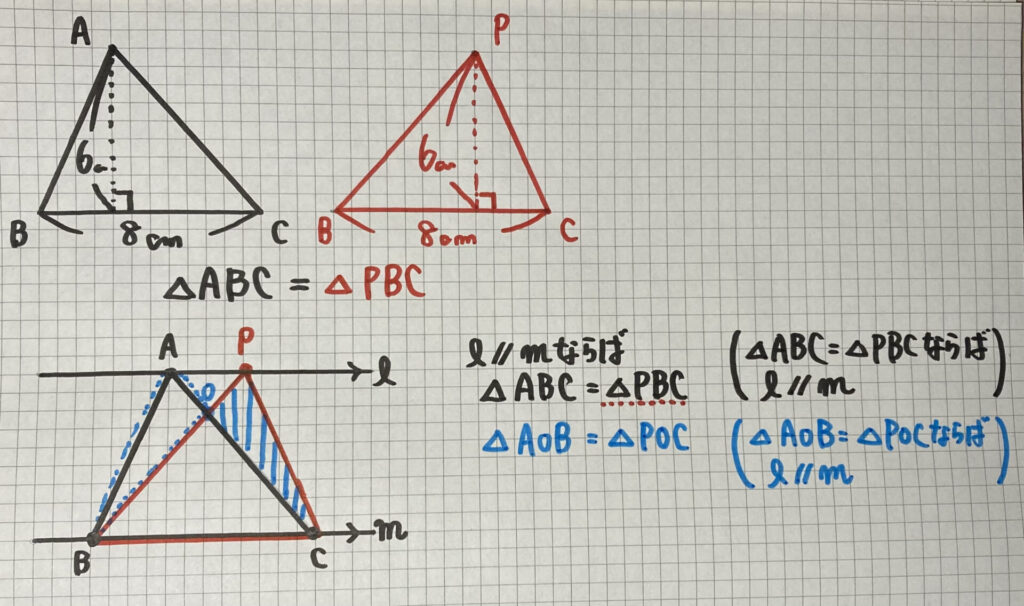
△ABCと△PBCは
どちらも
「底辺8cm」「高さ6cm」で
面積が等しくなりますね
先ほどの
2つの三角形を
辺BCを重ねて書くと
ノートの下のような
図になります
ここで大切なことは
ここで
もう1つ
ポイントがあります
理由を簡単に下にまとめますね
△AOB=△ABC−△OBC
△POC=△PBC−△OBC
ですね
ここで先ほどやった
△ABC=△PBCを
利用すると
△AOB=△POC
となりますね
等積変形の作図
では実際に
「等積変形」を利用した
作図をやっていきましょう
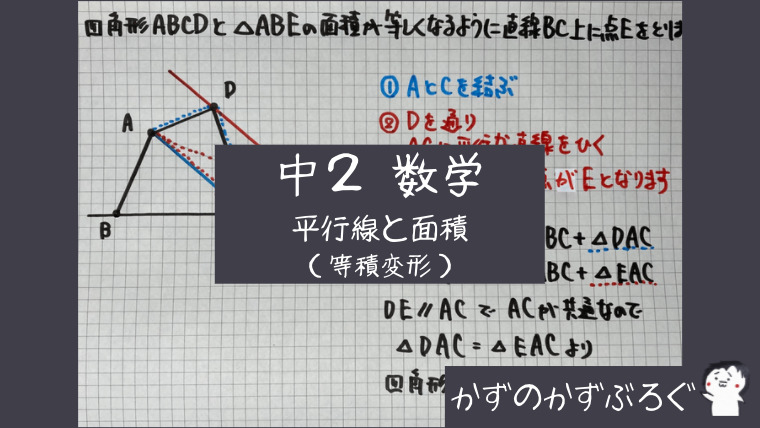
①四角形から三角形を作る
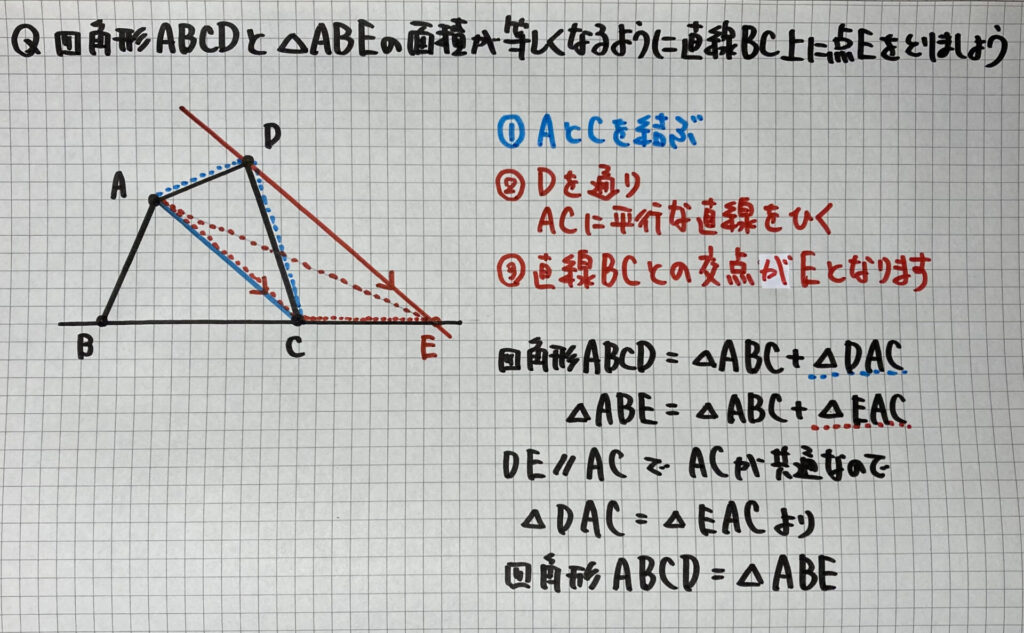
教科書や問題集
学校のテストによく出てくる
等積変形の作図の
「基本の問題」です
この問題を
理解しないと
次からの問題を
解くのが大変になるので
しっかりと確認しましょう
ノートにまとめていますが
ポイントは
AとCを結び
四角形ABCD=△ABC+△DAC
にすることです
- AとCを結ぶ
- Dを通りACに平行な直線を引く
- 直線BCと平行線の交点がEとなります
(点Dを平行線上で点Eにスライドするイメージです)
②折れ線を直線にする
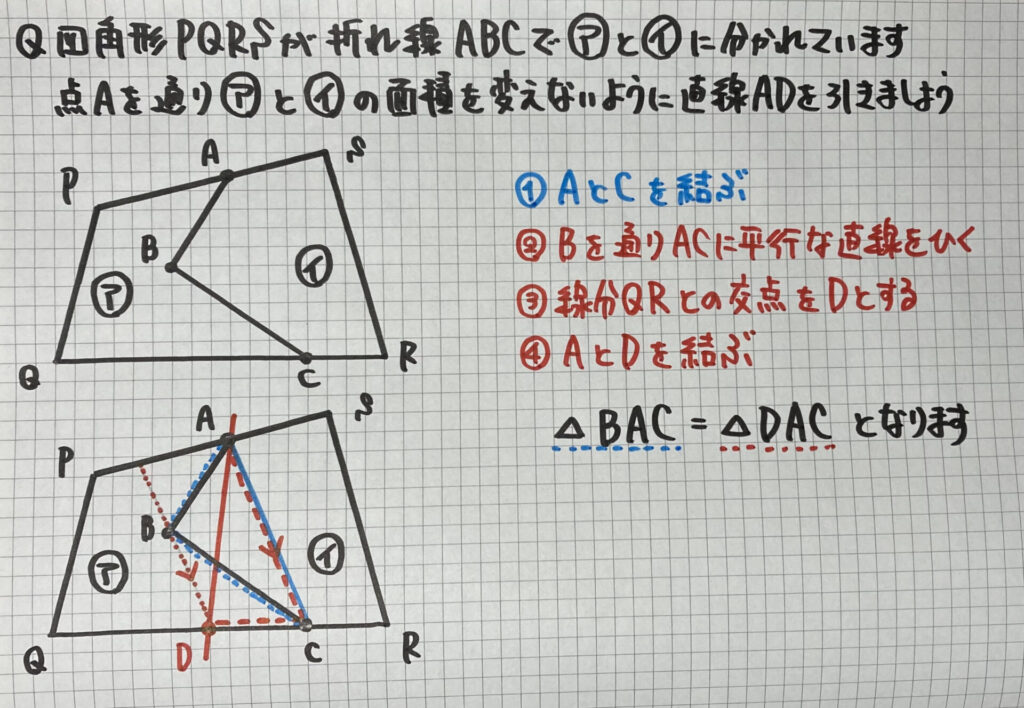
こちらも
有名な問題です
先ほどと
向きが違うことに注意してください
ノートを
見てもらうと
分かると思いますが
先ほどの問題と
流れは同じですので
数回、練習すれば
大丈夫ですよ
③五角形から三角形を作る
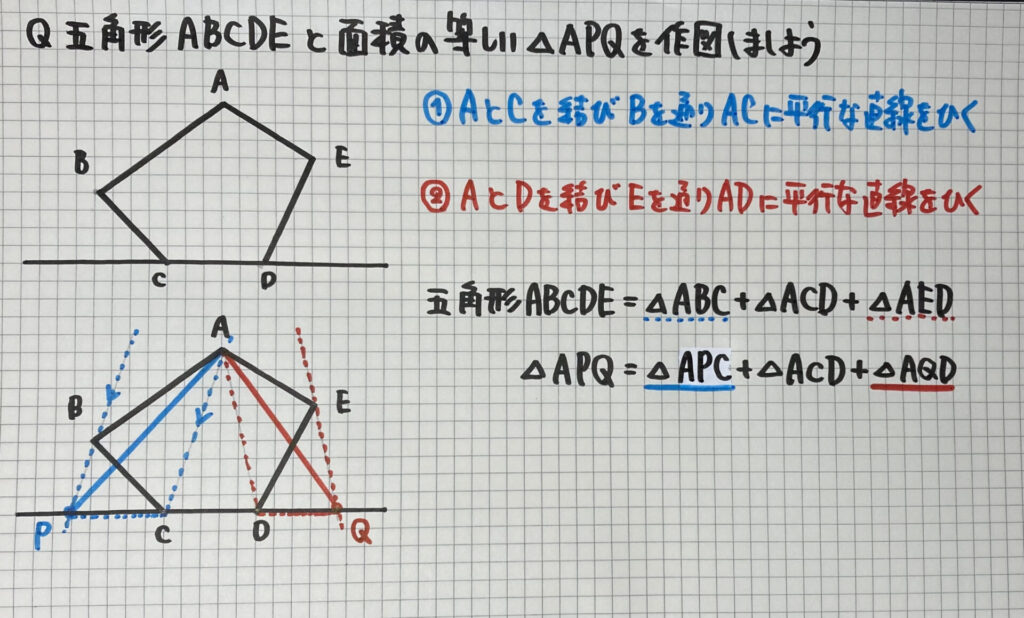
この問題は
一見難しそうに
見えますが
①②の問題と違って
1回だけの
「等積変形」を
左右で
2回行っています
ポイントは
AとC AとD
を結び
五角形ABCDE=△ABC+△ACD+△AED
にすることです
等積変形の利用①(平行四辺形の中の三角形)
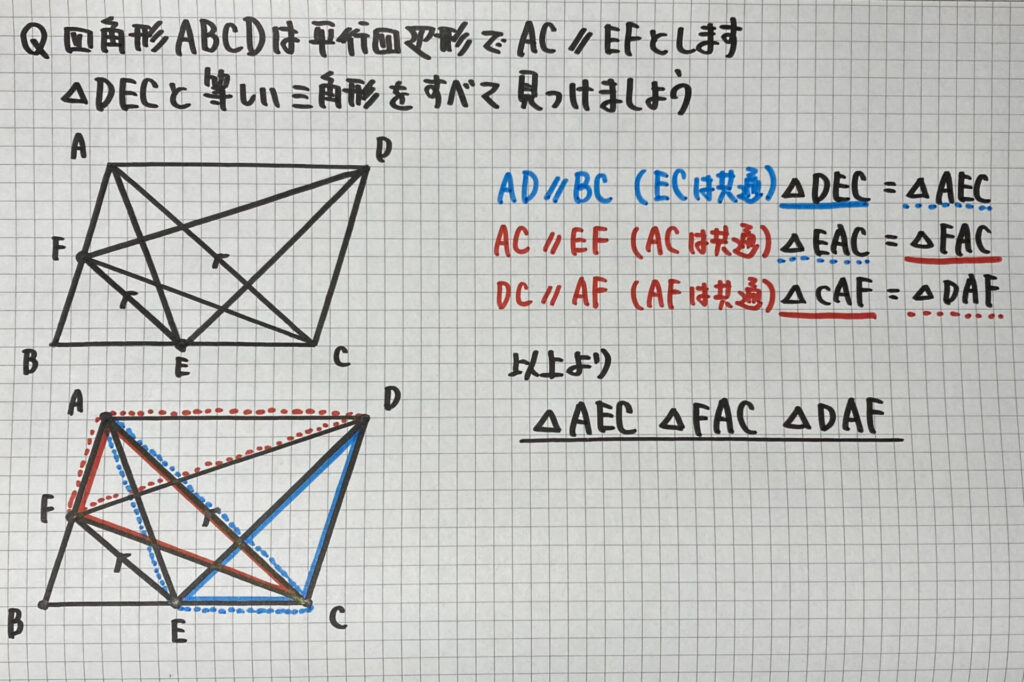
こちらも
「等積変形」
といえば…の問題です
分かりにくい人は
1つ1つ順番に「三角形」に
色をつけていくと
見やすくなると
思います
等積変形の利用②(面積を求める)
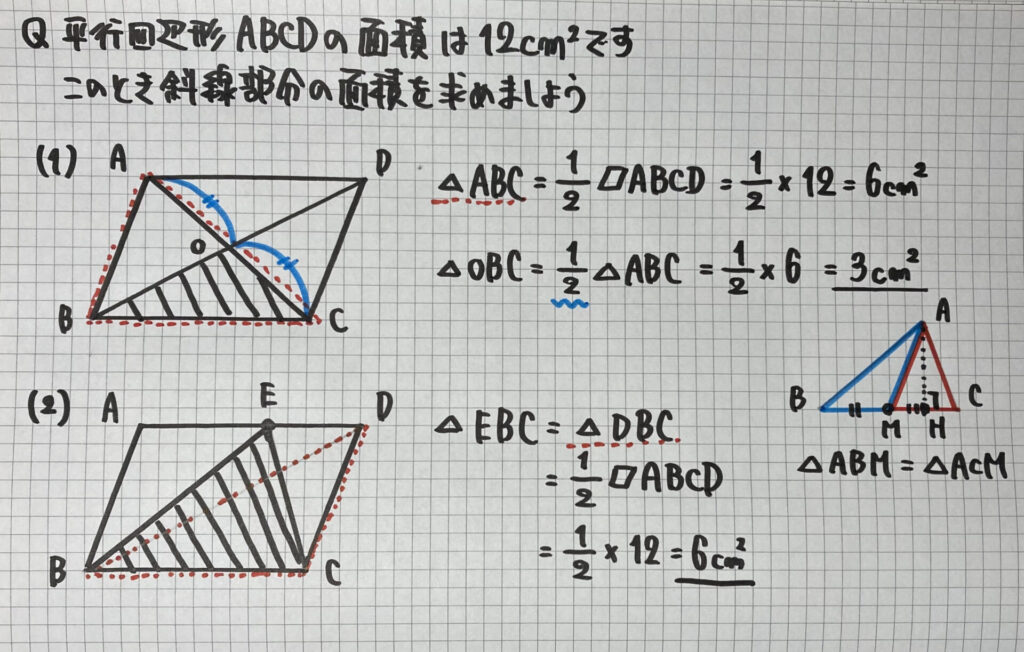
「等積変形」
を利用して
「面積を求める」
ことができます
(1)は
平行四辺形の性質
- 対角線はそれぞれの中点で交わる
を使うだけで
△OBCは
になることが分かりますね
ノートの右に
まとめていますが
- 「底辺の長さ」が等しい
- 「高さ」が共通な
三角形は面積が等しくなります
(2)は
「等積変形」を
利用すると
とても簡単ですね
AD//BCなので
△EBC=△DBC
(点Eを点Dの位置まで動かします)
すると
「面積は平行四辺形の半分」
になりますね
平行線と面積(等積変形)のまとめ

・等積変形

1つの直線(m)上の2点B,Cと
その直線(ℓ)の同じ側にある2点A,Pについて
- ℓ//mならば△ABC=△PBC
- △ABC=△PBCならばℓ//m
また、△AOB=△POCもポイントです
・等積変形の作図
四角形ABCD=△ABEを作図する時
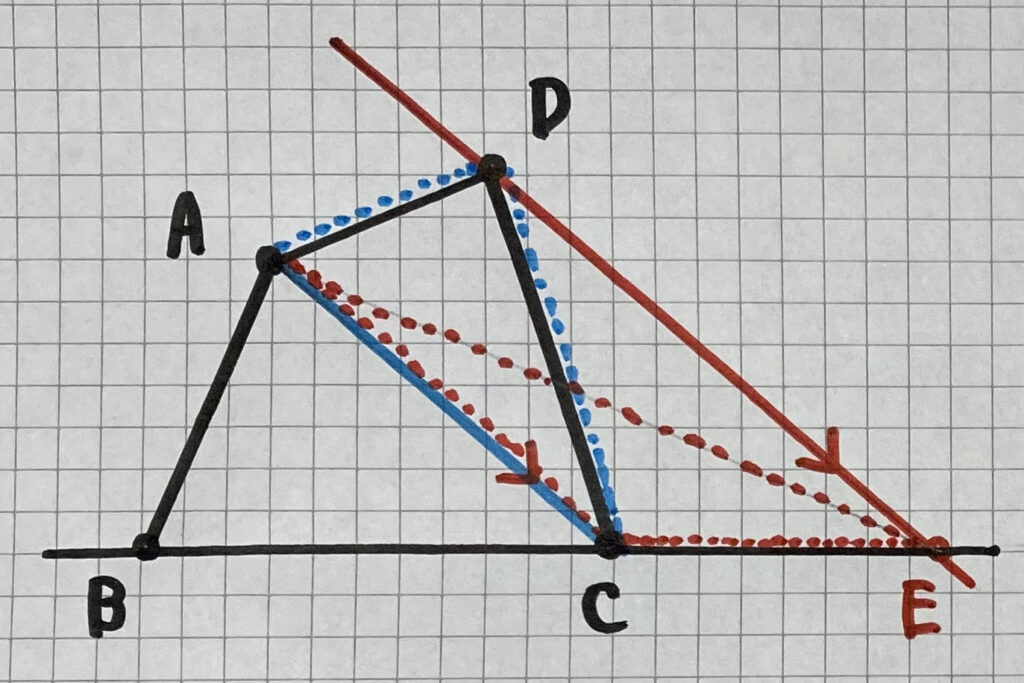
- AとCを結ぶ
- Dを通りACに平行な直線を引く
- 直線BCと平行線の交点がEとなります
(点Dを平行線上で点Eにスライドするイメージです)
・平行四辺形の中の等積変形
平行線に注目して
「共通な底辺を持つ三角形」
を探しましょう
以上、「数学嫌いな人が、
数学を楽しく好きになって欲しい」
かずのかずぶろぐでした