前回までに
特別な三角形として
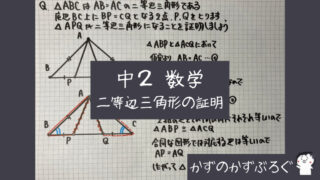
「二等辺三角形」
「正三角形」を学習しました
こちらで
確認してくださいね
今回は
「直角三角形」
について
一緒に見ていきましょう
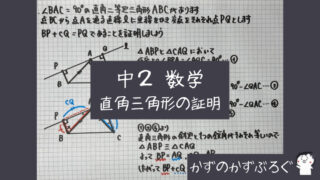
直角三角形の合同条件
「直角三角形」は
三角形なので
以前学習した
3つの合同条件を
使うことができます
さらに2つ
「直角三角形の合同条件」
があります
では
こららの
合同条件の証明を
実際にやってみましょう
①の証明

ノートに証明しましたが
もう少し簡単に
まとめてみますね
直角三角形なので
(角を簡単な形で書きます)
$\angle C$=$\angle F$=$90°$
そして「仮定」で
$\angle B$=$\angle E$とあるので
残りの角
$\angle A$=$\angle D$
となりますね
また「仮定」で
AB=DE(斜辺が等しい)
とあるので
「1組の辺とその両端の角が…」
で合同が証明できました
②の証明
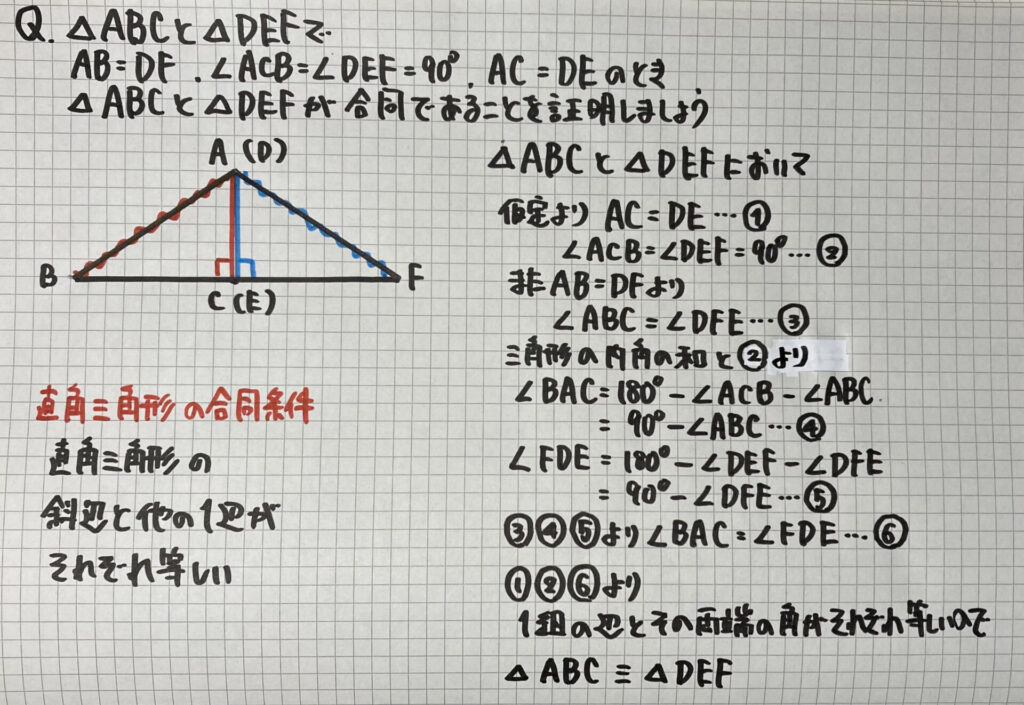
こちらの証明も
もう少し簡単に
まとめますね
直角三角形なので
(角を簡単な形で書きます)
$\angle C$=$\angle E$=$90°$
そして「仮定」で
AB=DFとあるので
△A(D)BFは
「二等辺三角形」で
$\angle B$=$\angle F$となり
残りの角
$\angle A$=$\angle D$
となります
また「仮定」で
AC=DE
とあるので
「1組の辺とその両端の角が…」
で合同が証明できました
これからは問題で
「直角三角形」があれば
①②をいちいち証明せずに
合同条件として
使うことができます
「合同条件を使った」証明①
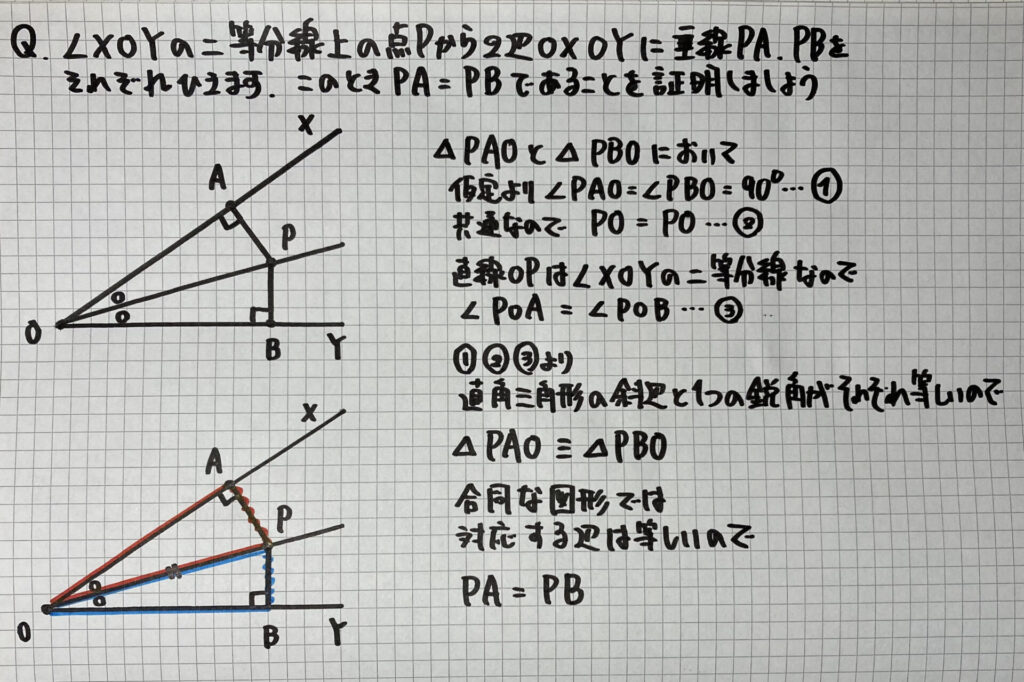
次に
「直角三角形の合同条件」を使った
証明の流れをまとめますね
- 直角(90°)を含む1組の三角形を探す
- 「斜辺が等しい」が言えるかを確認する
- 等しい「1つの鋭角(他の1辺)」を確認する
- 合同条件を書く(「直角三角形の」を書き忘れないように注意)
- △…≡△…
「合同条件を使った」証明②
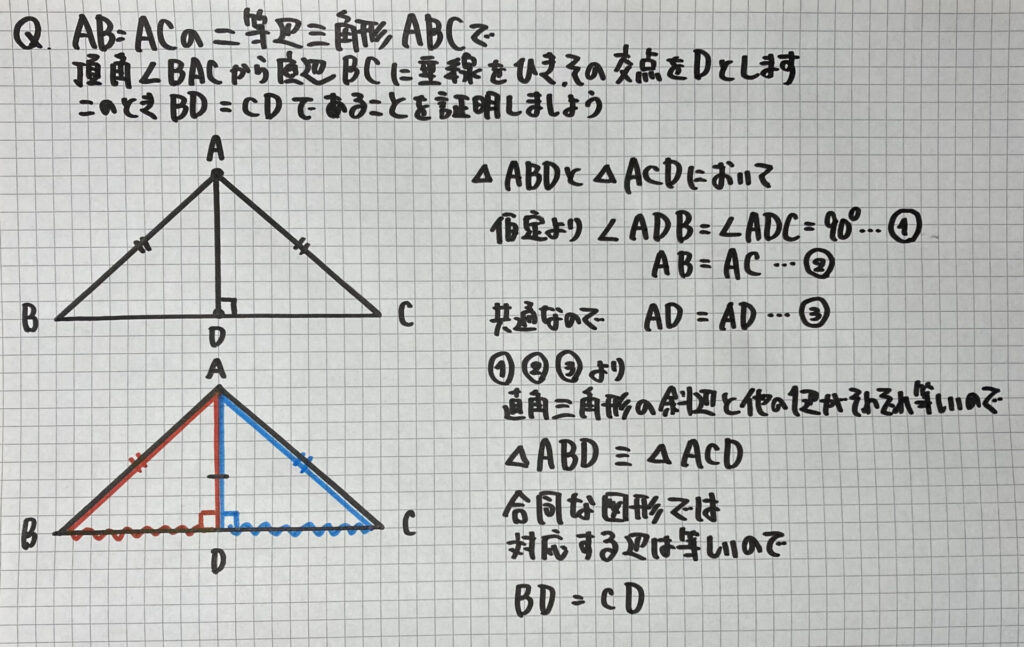
この問題は
- 垂線…直角(90°)がある
- 斜辺…「仮定」に二等辺三角形とあるので等しい
があるので
直角三角形の合同条件を使うことができますね
直角三角形の合同条件のまとめ

・直角三角形の合同条件
3種類の三角形の合同条件
+
直角三角形の
- 斜辺と1つの鋭角が、それぞれ等しい
- 斜辺と他の1辺が、それぞれ等しい
・直角三角形の合同条件を使った証明
- 直角(90°)を含む1組の三角形を探す
- 「斜辺が等しい」が言えるかを確認する
- 等しい「1つの鋭角(他の1辺)」を確認する
- 合同条件を書く(「直角三角形の」を書き忘れないように注意)
- △…≡△…
以上、「数学嫌いな人が、
数学を楽しく好きになって欲しい」
かずのかずぶろぐでした