少し前に
「証明のしくみ…」で
「仮定と結論」を
学習しましたね
こちらで
確認してくださいね

今回は、その
「仮定と結論」を
利用した「逆・反例」
を学習します
また、前回の
「二等辺三角形」
のさらに特別な三角形
「正三角形」について
一緒に見ていきましょう
逆・反例

まず言葉の説明です
少し復習しましょう
<ならば>を目印にして
「仮定」ならば「結論」
でしたね
逆は「仮定」と「結論」を入れかえます
「A」ならば「B」
↓
「B」ならば「A」となります
逆が「正しい」かを調べるには
「反例」がないかを調べましょう
反例を1つでも示せば
「正しくない」ことが説明できます
「正三角形」の証明
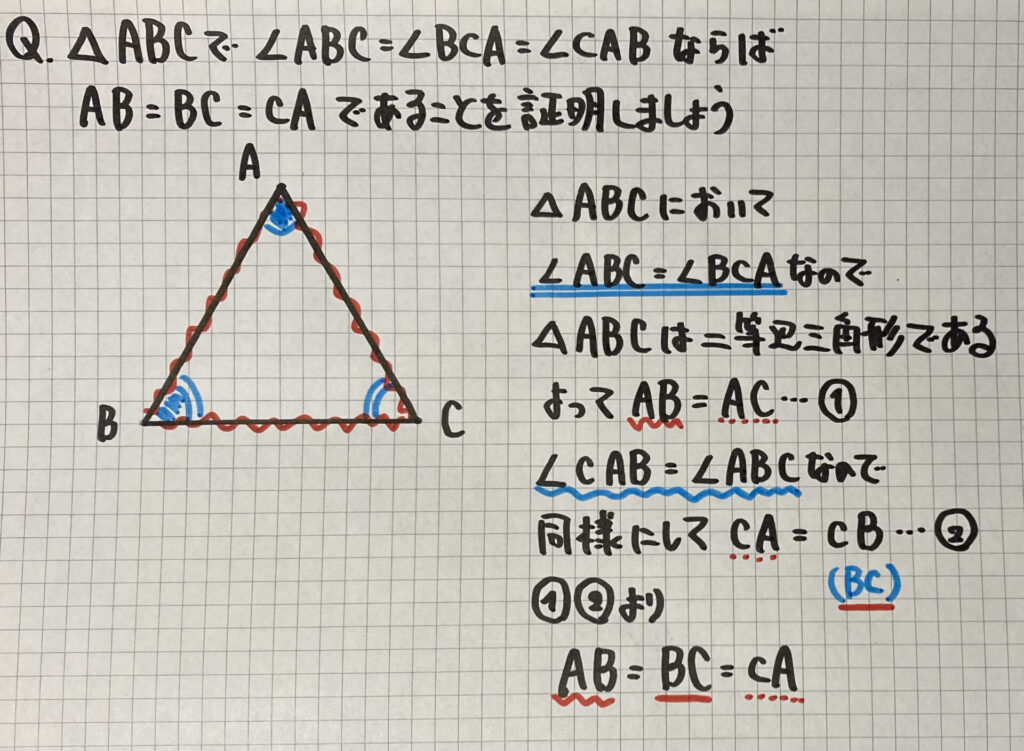
底角が等しい
↓
二等辺三角形
↓
2辺が等しい
を2回行い
「全ての辺が等しいこと」
を証明しています
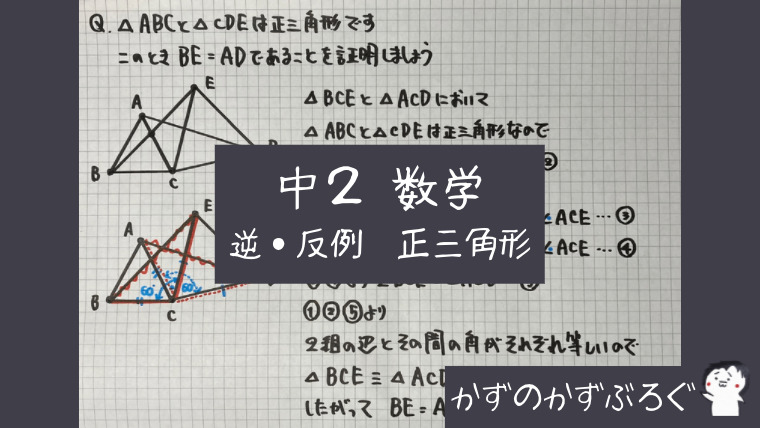
「正三角形を使った」証明
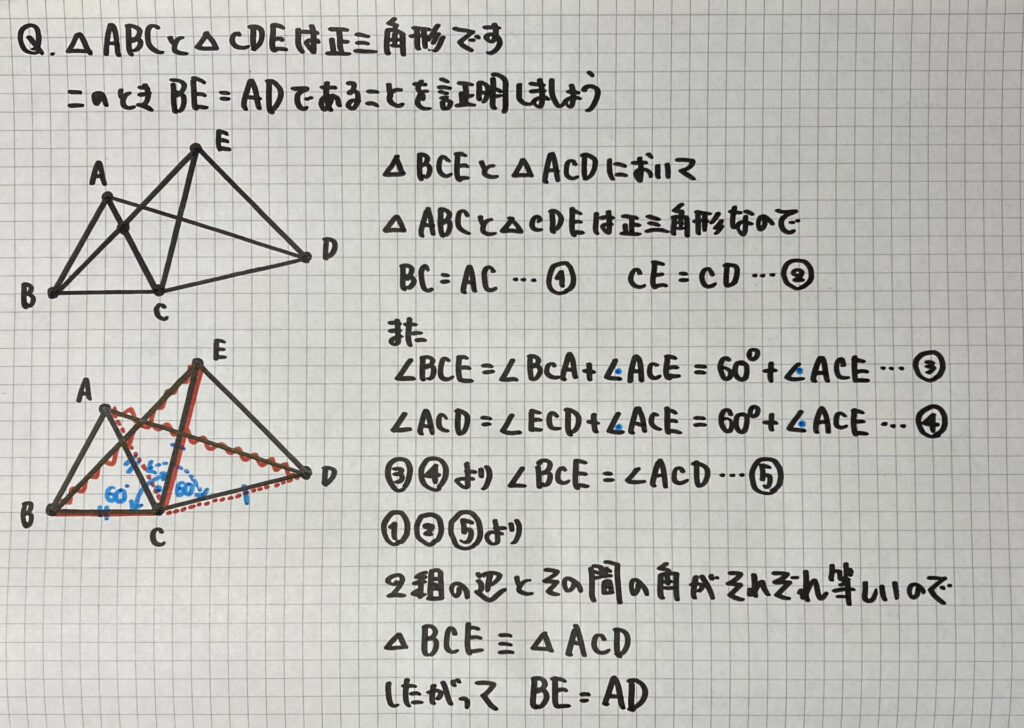
「正三角形が2つ並ぶ」
よく出てくる問題です
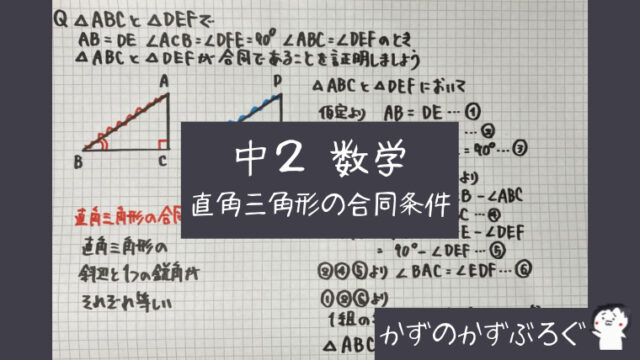
対応する辺の長さが等しい証明
は「三角形の合同の証明」
で学習しましたね
- 対応する辺に印を入れる
- 印を入れた辺を含む三角形を1組探す
- 仮定を図に書き入れる
- 3つの「三角形の合同条件」のどれが当てはまるか考える(①の結論は使えません)
- 三角形の合同を証明する
- 「したがって…」で結論に導く
この問題では
合同な三角形が「重なっている」ので
最初は少し見つけるのが
難しく感じるかもしれません
ノートでは
赤の「実線」と「点線」にしていますが
見えにくい時は
色を変えて三角形を縁取ると
見やすくなりますよ
証明を書くときのポイントは
正三角形
- 等しい辺を2組
- 60°の利用
することです
角度については
計算式で表します
よく出てくる形なので
何回か練習しておきましょう
$\angle BCE$=$\angle BCA$+$\angle ACE$と
$\angle ACD$=$\angle ECD$+$\angle ACE$は
正三角形の性質より
$\angle BCA$=$\angle ECD$=$60°$
計算すると
どちらも
$60°$+$\angle ACE$となるので
$\angle BCE$=$\angle ACD$
と表すことができます
「正三角形を使った角」の問題
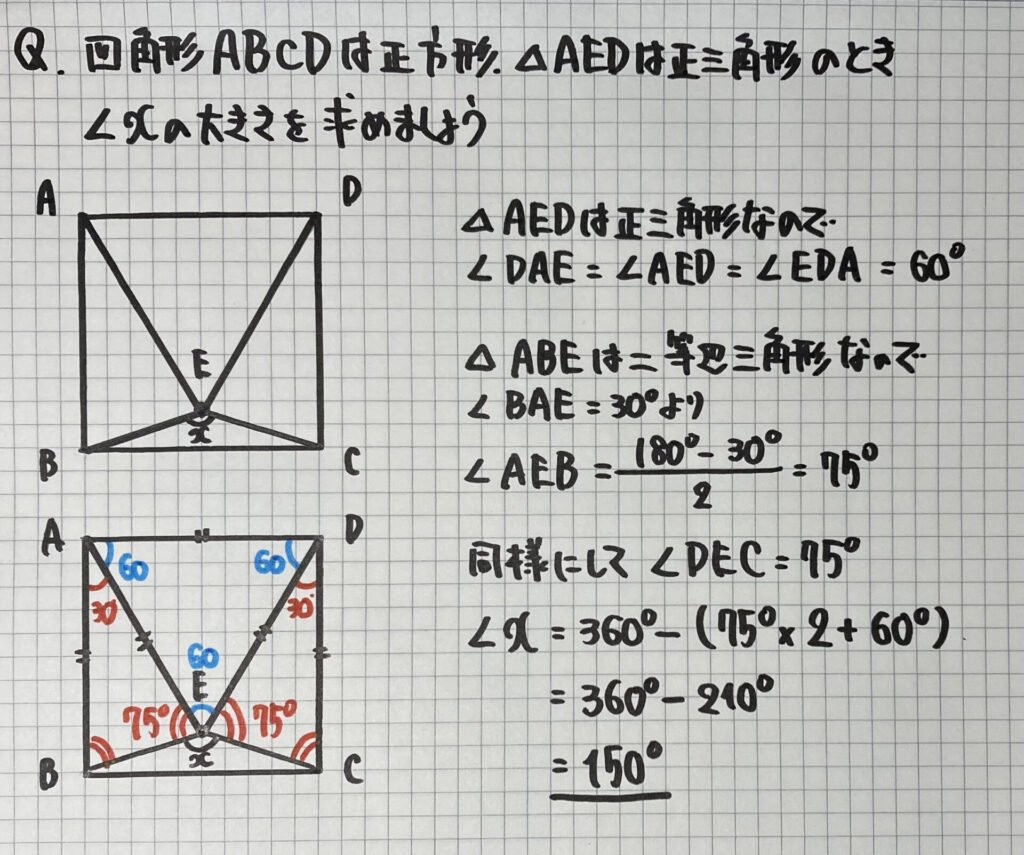
角度を求める問題は
問題文の条件
(正方形、二等辺三角形等)を
まず書き入れます
そして
この問題のポイントは
△ABE(△DEC)が
「二等辺三角形である」こと
を見つけることです
逆・反例 正三角形のまとめ

・逆
2つのことがらが
「仮定」と「結論」を入れかえた関係にある時
一方を他方の「逆」と言います
・反例
あることがらの仮定にあてはめるもののうち
結論が成り立たない場合の例のこと
・正三角形
二等辺三角形の特別なもの
(二等辺三角形の性質を全て持っている)
以上、「数学嫌いな人が、
数学を楽しく好きになって欲しい」
かずのかずぶろぐでした