前回まで
学習してきた
「一次関数の利用」
として
「速さ」
「バネの長さ」
「動点」の
問題を学習します
中1の
「比例 反比例の利用」
で似た問題を
学習しましたので
参考にしてください
では一緒に
やっていきましょう
「速さ」の問題
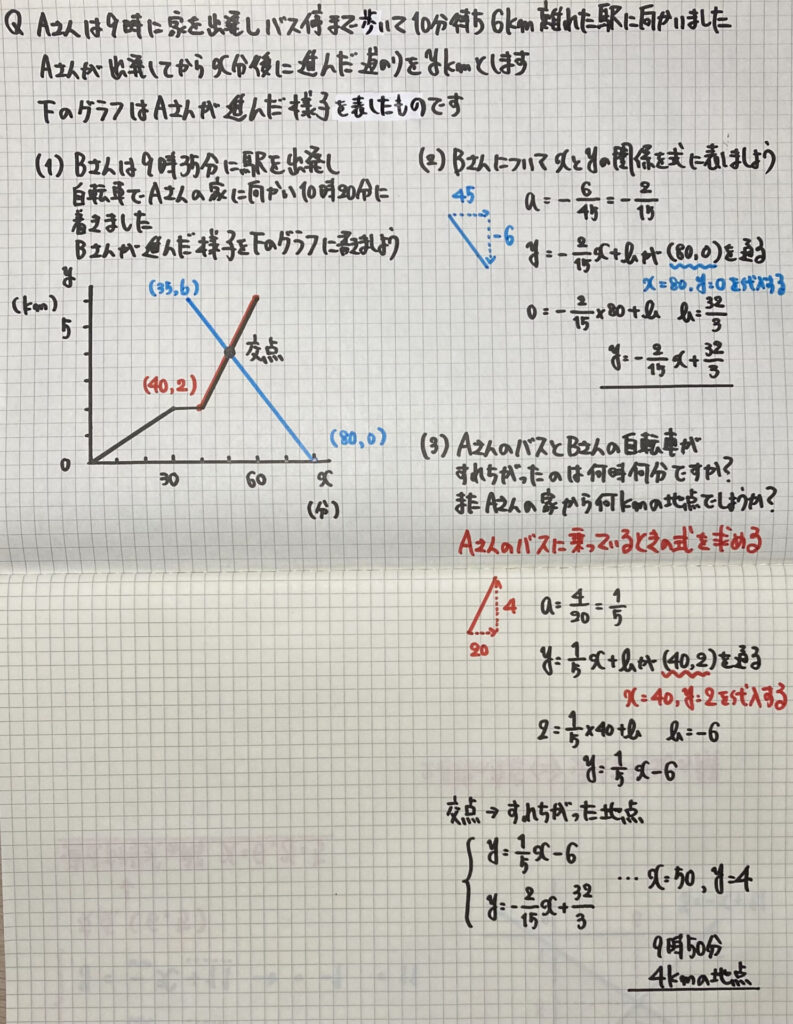
AさんとBさん
2人の動きを
グラフに表した問題です
いつもの
「一次関数」の
$x$と$y$の
「目盛りの大きさ」が
違うので気をつけましょう
下にポイントを
まとめました
$y=0$…Aさんの家
$y=2$…バス停
$y=6$…駅
を表しています
Aさんの動き
原点(0,0)から右上に進む折れ線
Bさんの動き
(35,6)から右下に進む直線
交点
AさんとBさんの
すれ違う(出会う)地点
直線の傾きは
「$\frac{yの増加量}{xの増加量}$」
=「$\frac{進んだ道のり}{進んだ時間}$」
となるので
最後の
交点を求める
「連立方程式」の計算は
省略していますので
がんばって
計算してみてください
「バネ」の問題

この問題の
ポイントは
ノートの左にある
「注!」です
問題文に
「…比例…」と
ありますが
3gでバネが19cm伸びていません
問題文だけでは
最初の「バネの長さ」は
分かりません
3gでバネの「長さ」が19cmになりました
(元がある長さのバネが伸びて19cmになっています)
ややこしい日本語ですが
間違えやすいので
気をつけましょう
- $\frac{yの増加量}{xの増加量}$=変化の割合(a)を求めてから$y=ax+b$に代入する
- $y=ax+b$に2組の$x$と$y$を代入して求める
①②の
どちらの方法でも
解くことができます
「動点」の問題
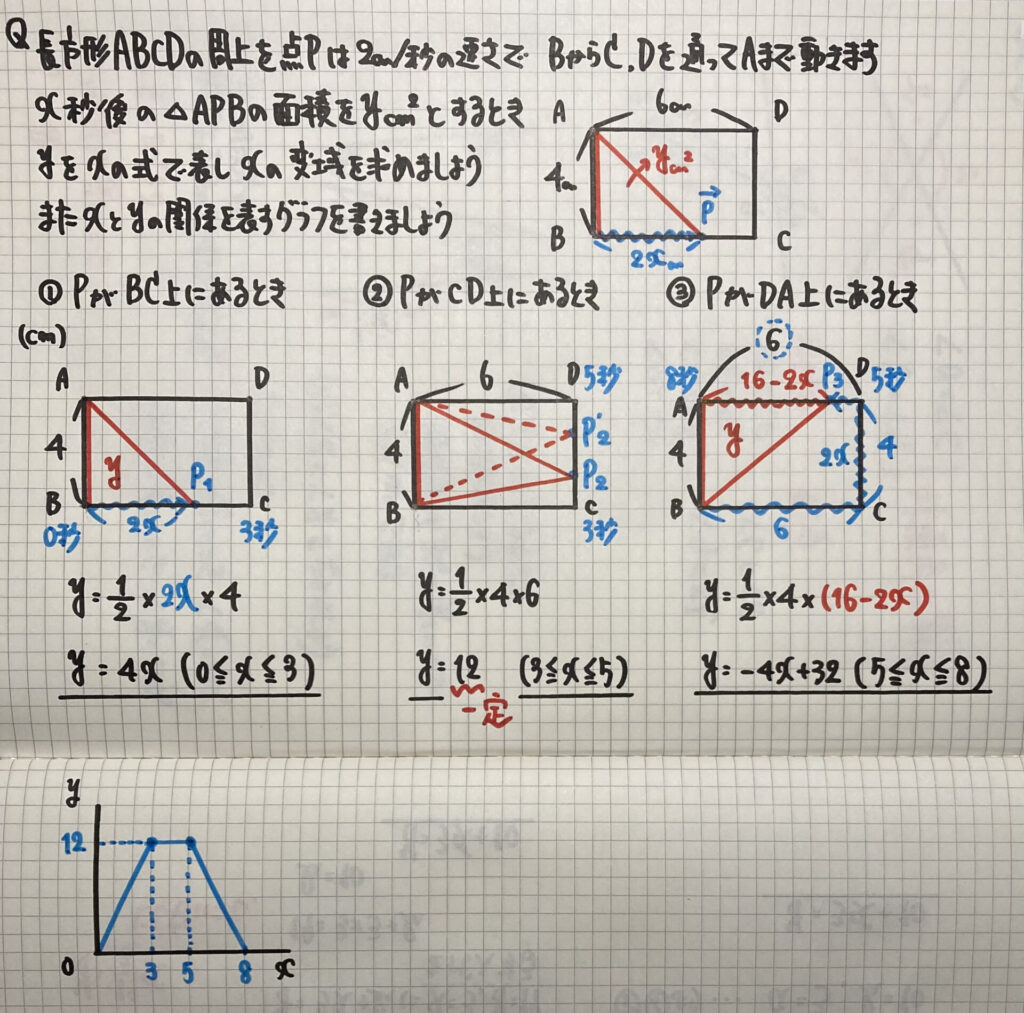
「数学」でよく出てくる
図形の上を動く点(動点)の問題です
三角形の形が
Pがいる辺によって
大きく3種類になります
Pが
- BC上
- CD上
- DA上
にある時です
この問題のポイントは
③PがDA上にある時の
APの長さは
$16−2x$cm
になるので
気をつけましょう
一次関数の利用のまとめ

・速さを表すグラフ
直線の傾き=速さ
・「バネの長さ」の問題
- $\frac{yの増加量}{xの増加量}$=変化の割合(a)を求めてから$y=ax+b$に代入する
- $y=ax+b$に2組の$x$と$y$を代入して求める
・「図形の上の動点」の問題
- 辺によっての場合分け(変域になります)
- 頂点に来るのがいつ(何秒後)
を調べましょう
以上、「数学嫌いな人が、
数学を楽しく好きになって欲しい」
かずのかずぶろぐでした