前回
「一次関数と変化の割合」
について学習しました
一次関数については
こちらで
確認してくださいね

今回は
一次関数の
「グラフと式」
について
一緒に見ていきましょう
一次関数のグラフ
傾きと切片(せっぺん)
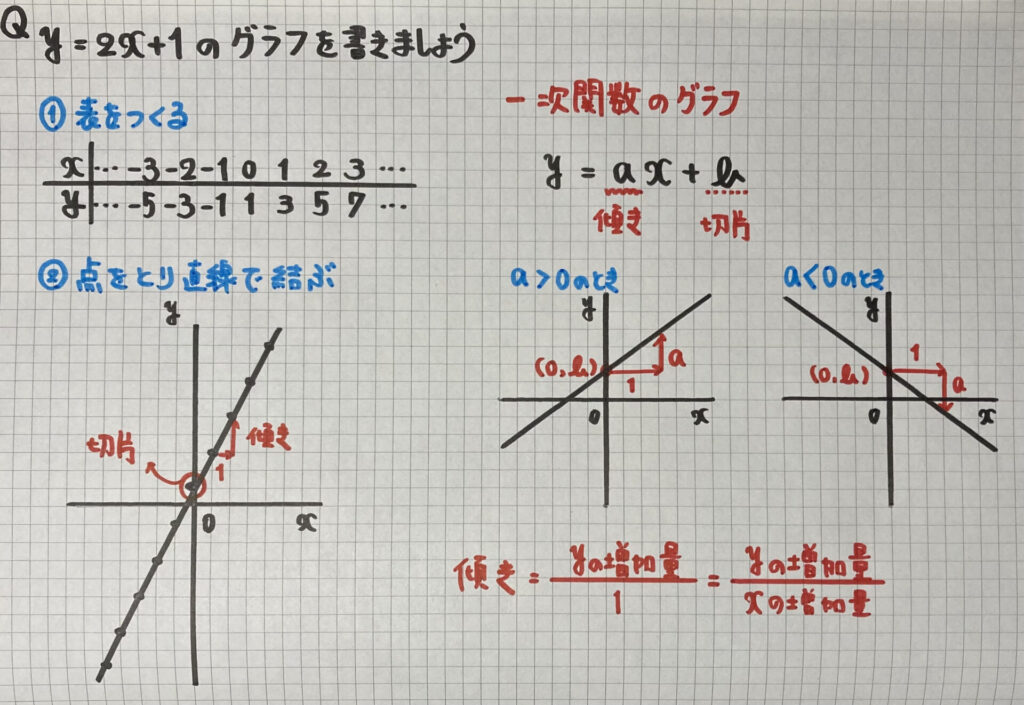
中1で学習した
「比例のグラフ」と
考え方は同じで
大丈夫です
- 表を作り$x$と$y$を求める
- 点をとり直線で結ぶ
ここで
新しい言葉が
出てきます
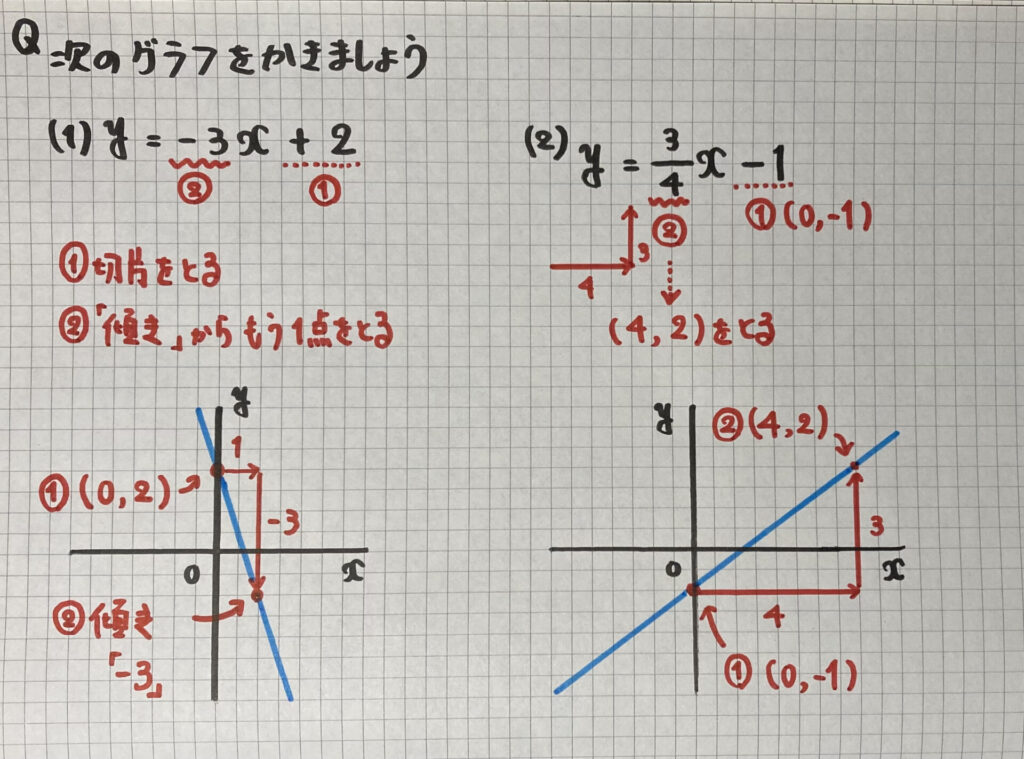
グラフの書き方
先ほどのように
$x$と$y$を表にして
点を打ち
直線で結ぶ
でもグラフを
書くことはできますが
大変ですよね
今回学習した
「傾き」と「切片」を使って
簡単に書くことが
できます
- 切片をとる($x$軸上)
- 「傾き」から、もう1点をとる
- 2点を直線で結ぶ
変域のあるグラフ
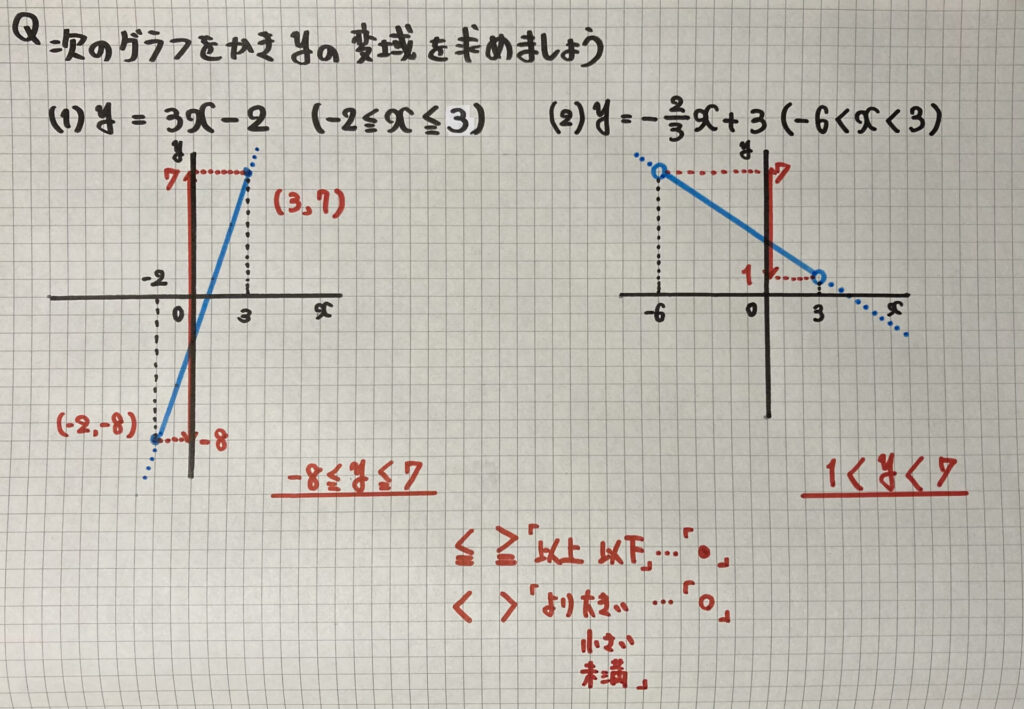
$x$と$y$に
「変域」があるグラフの
書き方についてです
①②は同じです
- 切片をとる($x$軸上)
- 「傾き」から、もう1点をとる
- 2点を点線で結ぶ
- $x$($y$)の変域の点をとる※
- 変域内を実線で結ぶ
(1)は
$x$の最小値と最大値が
$y$の最小値と最大値に
対応しています
$x$の最小(大)
を代入すると
$y$の最小(大)
を求めることができます
(2)は
$x$の最小値と最大値が
$y$の最大値と最小値に
対応しています
$x$の最小
を代入すると
$y$の最大
を求めることができます

言葉にすると
ややこしくなりますね
大切なことは
一次関数の式を求める
「一次関数の式を求める」
問題には大きく
3つのパターン
- 傾きと切片がわかる
- 傾きと1点の座標がわかる
- 2点の座標がわかる
があります
(1)は
簡単です
- 傾き=$a$ 切片=$b$を$y=ax+b$に代入する
そのまま
代入するだけですね
(2)は
- 傾き=$a$ $y=ax+b$に代入する
- 点の座標の$x$と$y$を代入して$b$を求める
$b$を求める必要がありますね

(3)は
2つの求め方が
あります
- $傾き(a)=\frac{yの増加量}{xの増加量}$で求める
- ①で求めた$a$と1つの点※の$x$と$y$座標を代入して$b$を求める
※代入するのは、どちらの点でも大丈夫です
- 1つの点の$x$と$y$座標を$y=ax+b$代入する
- もう1つの点の$x$と$y$座標を$y’=ax’+b$代入する
- ①と②で代入した式を連立させて$a$と$b$を求める
どちらでも
求めることは
できるのですが
<2>の連立方程式だと
- 求めるのに時間がかかる
- 方程式の計算に時間がかかる
ので
<2>の連立方程式のやり方は
時だけ使いましょう
練習問題

(1)は、代入して終了です
(2)は
「変化の割合が…」と出てきます
傾き=$\frac{yの増加量}{xの増加量}$=変化の割合なので
変化の割合=$a$に
代入しましょう
(3)は
「傾き」という
言葉はありませんが
「$x$の増加量」と
「$y$の増加量」があるので
$傾き(a)=\frac{yの増加量}{xの増加量}$
で求めましょう

(4)は
「傾き」は
ありませんが
$y=−\frac{2}{5}x +3$と
「平行」とあります
この性質を使って
$傾き(a)=−\frac{2}{5}$を
使って求めましょう
(5)は
- 「傾き」を求めて、1点を代入する
- 連立方程式を使う
どちらで求めても
大丈夫です
今回は
「連立方程式で求める」
練習をしました
一次関数のグラフと式のまとめ

・傾きと切片(せっぺん)
$y=ax+b$の
$a$を傾き
$b$を切片
と言います
・傾き
$a=\frac{yの増加量}{xの増加量}$
・切片
$x=0$の時の
$y$の値です
(グラフでは$x$軸との交点です)
・グラフの書き方
- 切片をとる($x$軸上)
- 「傾き」から、もう1点をとる
- 2点を直線で結ぶ
・変域のあるグラフの書き方
- 切片をとる($x$軸上)
- 「傾き」から、もう1点をとる
- 2点を点線で結ぶ
- $x$($y$)の変域の点をとる※
- 変域内を実線で結ぶ
※点の書き方
≦(≧)の時…「●」
<(>)の時…「○」
・変域を求める問題
グラフを書いてから求める
・式を求める問題は3種類
- 傾きと切片がわかる
- 傾きと1点の座標がわかる
- 2点の座標がわかる
・式を求める問題の求め方
問題文から
- 傾き 切片
- 傾き と $x$と$y$の座標
- 2組の$x$と$y$の座標
を見つけて
$y=ax+b$に代入する
・平行な2直線
「傾き」が等しくなる
以上、「数学嫌いな人が、
数学を楽しく好きになって欲しい」
かずのかずぶろぐでした