今回は
前回の「連立方程式の文章題③」

に続いて
文章題④として
「速さ」について
一緒に見ていきましょう
基本的には
中1で学習した

こちらと
同じ考え方で
大丈夫です
ちなみに
計算については

こちらで
確認してくださいね
速さの公式
大丈夫ですか?
ポイントを
まとめておきます
- 速さ=道のり÷時間=$\frac{道のり}{時間}$
- 時間=道のり÷速さ=$\frac{道のり}{速さ}$
- 道のり=速さ×時間
方程式を立てるときは
②③を使うことが多いです
- 単位は「速さ」に合わせる
新しい速さの表し方です
- 時速$x$km=$x$km/時
- 分速$y$m=$y$m/分
- 秒速$z$cm=$z$cm/秒
「速さが変わる」問題

この問題の
ポイントは2点です
- 単位をそろえること
- 上り、下りを間違えない
まず時間を
きちんと直します
3時間48分=$3\frac{48}{60}$=$3\frac{4}{5}$=$\frac{19}{5}$時間
「約分」
「帯分数を仮分数にする」ことに
気をつけましょうね
次に式に注目してください
$\begin{eqnarray}\left\{\begin{array}{l}① \\②\end{array}\right.\end{eqnarray}$
①と②の式の
$x$と$y$の順番が
逆になっている
ことに気をつけましょう
「出会う・追いつく」問題①

問題文の
「道のりが(m)」
「時間が(分)」に
なっているので
「速さ」は
「分速(m/分)」で
表しましょう
次に式の立て方です
①の式は
Aの進んだ道のり+Bの進んだ道のり=1800
(進んだ道のりの和)
②の式は
Aの進んだ道のり−Bの進んだ道のり=1800
(進んだ道のりの差)
で立式しています
「出会う・追いつく」問題②

学校のテストや
問題集によく出る
「池の周り」の問題です
やり方は
先ほどの
「出会う・追いつく」問題
と同じです
①の真っ直ぐな道を
丸めて考えるだけです
「列車の通過」の問題
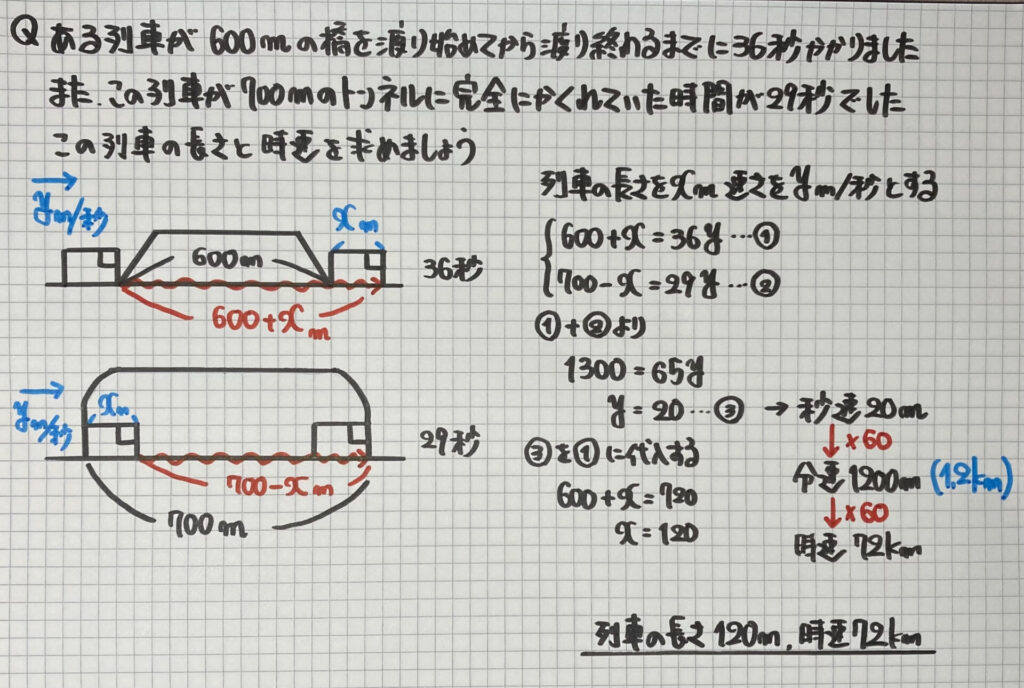
最後に
「列車の通過」
の問題です
この問題のポイントは
ことです
そして、問題では
「時速」を求めなさい
となっていますが
問題文の
「道のりが(m)」
「時間が(秒)」に
なっているので
「速さ」は
「秒速(m/秒)」で
式を立てましょう
最後に
秒速→(×60)→分速→(×60)→時速
で「速さ」を
求めています
連立方程式の文章題④速さのまとめ

・「速さが変わる」問題
- 単位をそろえること
- 上り、下りを間違えない
・「出会う 追いつく」問題
- 進んだ道のりの和
- 進んだ道のりの差
で式を立てる
・「池の周り」の問題
真っ直ぐな道を
「丸めて」考えましょう
・「列車の通過」の問題
- 「渡り始めてから渡り終わるまで…」
→列車の長さを道のりに足す
- 「完全にかくれていた…」
→列車の長さを道のりから引く
以上、「数学嫌いな人が、
数学を楽しく好きになって欲しい」
かずのかずぶろぐでした