前回、二等辺三角形の「角」
について学習しましたね
こちらで
確認してくださいね
今回は
二等辺三角形の「証明」
について学習していきましょう
定理の証明①
前回も学習しましたが
復習しておきますね

まず
自分で行ったこと
$\angle A$の角の二等分線を底辺BCにひき交点をDとする
を書きましょう
すると
△ABDと△ACD
を作ることができました
この三角形の合同を
証明すると
2つの「定理」
合同な図形では
対応する角の大きさは等しいので
$\angle ABC$=$\angle ACB(ABD)$
「二等辺三角形の
2つの底角は等しい」
合同な図形では
対応する
角の大きさ(辺の長さ)は等しいので
($\angle BDC$=180°<一直線>より)
- $\angle ADB$=$\angle ADC$=90°
- $BD=CD$ となり
「二等辺三角形の
頂角の二等分線は底辺を垂直に二等分する」
を証明することができました
これらの定理は
「証明の問題」以外でも
使うことが出てきます
問題で「二等辺三角形」
があれば下の
①②を必ずやってから
問題を解きましょう
- 底角が等しいことを使う
- 頂角の二等分線を引く→底辺を垂直に二等分する
- 90°ができる
- 底辺との交点が、底辺の中点となる
定理の証明②

先ほどの問題と
似ている問題です
こちらの形でテストに
出ることがあるので
確認しておいてくださいね
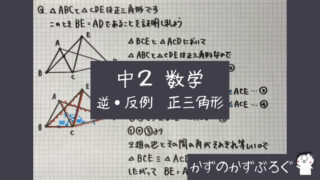
二等辺三角形の証明①

この問題は
合同な三角形を使わない
で証明できる問題です
いくつかの式から等式を作る
よく出てくる形なので
$\angle ABC$=$\angle ACB$…①
$\angle DBC$=$\frac{1}{2}$$\angle ABC$…②
$\angle DCB$=$\frac{1}{2}$$\angle ACB$…③
①②③より
$\angle DBC$=$\angle DCB$
この流れはしっかり
確認してくださいね
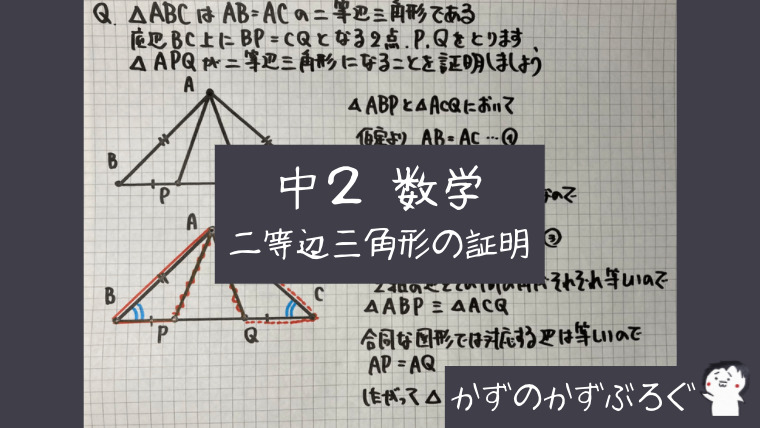
二等辺三角形の証明②
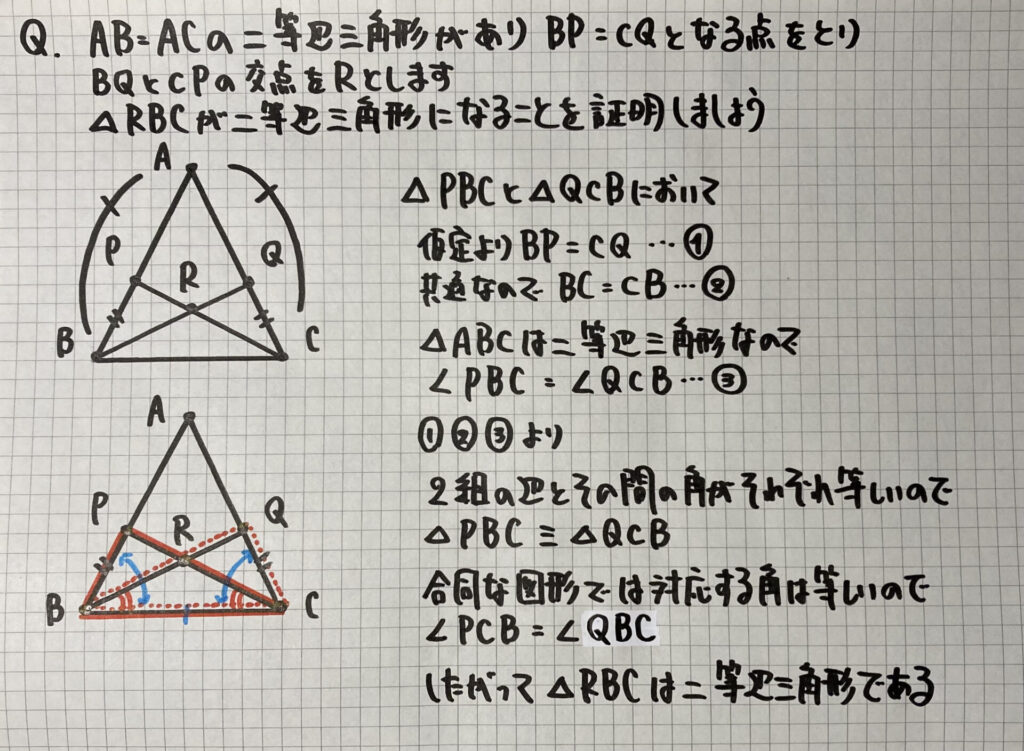
①の問題と似た問題ですが
角の二等分線ではなく
「仮定」がBP=CQになっています
そして「三角形の合同」を
利用します
- 合同な三角形を証明する
- 対応する角は等しい
- その等しい角を持った三角形は二等辺三角形
二等辺三角形の証明③
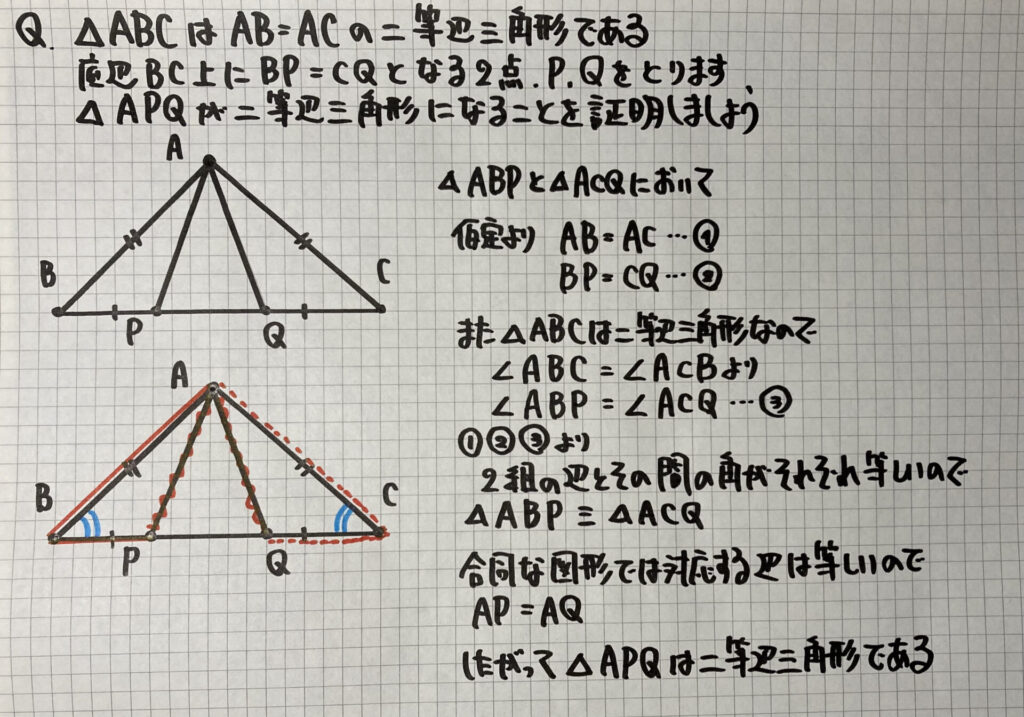
この問題も②と
同じように
「三角形の合同」を
利用します
①と違う点は
対応する「辺」を使って
証明しています
- 合同な三角形を証明する
- 対応する辺は等しい
- その等しい辺を持った三角形は二等辺三角形
教科書や問題集
テストによく出てくる
問題ですので
しっかり
練習しておきましょうね
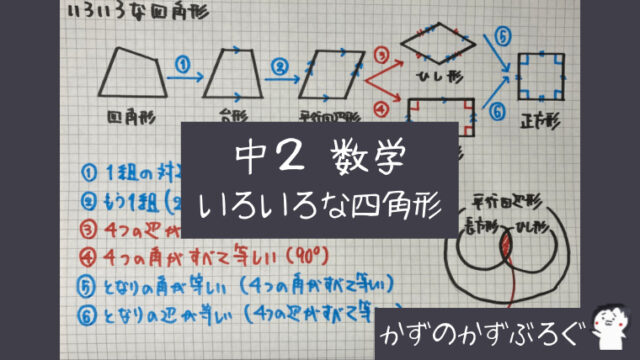
二等辺三角形の証明のまとめ

・(証明以外で)二等辺三角形がある時
- 底角が等しいことを使う
- 頂角の二等分線を引く→底辺を垂直に二等分する
- 90°ができる
- 底辺との交点が、底辺の中点となる
・二等辺三角形の証明
- 合同な三角形でなく角を利用
- 合同な三角形を利用
する場合があります
・合同を利用する証明
- 合同な三角形を証明する
- 対応する角(辺)は等しい
- その等しい角(辺)を持った三角形は二等辺三角形
以上、「数学嫌いな人が、
数学を楽しく好きになって欲しい」
かずのかずぶろぐでした